itle

Цели: разъяснить смысл слов «теорема» и «доказательство теоремы»; сформулировать и доказать первый признак равенства треугольников.

Ход урока

I. Актуализация опорных знаний.

Вопросы к учащимся:

1. Повторить определение смежных углов и их свойство.

2. Повторить определение вертикальных углов и их свойство.

3. Вспомнить определение равных фигур, биссектрисы угла.

4. Вспомнить, какой угол называется острым, прямым, тупым.

5. Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников.

II. Объяснение нового материала.

1. Разъяснение смысла слов «теорема» и «доказательство теоремы», так как с этими понятиями учащиеся встречаются впервые.

В геометрии каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

2. Напомнить учащимся, что приведенные ранее рассуждения о свойстве смежных и о равенстве вертикальных углов были доказательствами теорем, хотя мы их еще так не называли.

3. Повторить с учащимися понятие равенства фигур (отрезков, углов, треугольников), используя при этом таблицы, модели, кодопозитивы.

4. Сформулировать и доказать теорему, выражающую первый признак равенства треугольников (это объясняет учитель).

5. После доказательства теоремы (пункта 15) учитель разъясняет смысл слова «признак», отметив, что доказанный признак дает возможность устанавливать равенство двух треугольников, не производя фактического наложения одного из них на другой, а сравнивая только некоторые элементы треугольника.

III. Закрепление изученного материала.

Желательно рассмотреть как можно больше задач, решаемых по готовым чертежам.

1. Решение задач (устно) по готовым чертежам на доске (учитель использует цветные мелки для выделения одним цветом равных элементов).

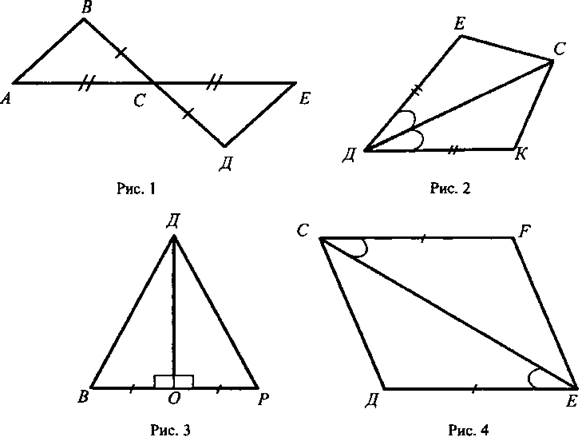
Задание: найдите пары равных треугольников (см. рис. 1-4) и докажите их равенство.

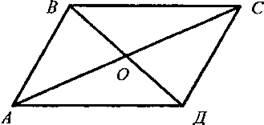
2. Решить задачу № 96 на доске и в тетрадях (по рис. 54).

Решение: Рассмотрим ΔАОВ и ΔДОС:

ОА = ОД (по условию); ОВ = ОС (по условию); ∠AOB = ∠ДОС (вертикальные углы равны) ⇒ ΔAОВ = ΔДОС (I признак, равны по двум сторонам и углу между ними).

Тогда ∠ДСО = ∠ABO = 74°.

∠АСД = ∠ACO + ∠ДСО = 36° + 74° = 110°.

Ответ: 110°.

3. Самостоятельно учащиеся решают задачу № 1:

Из точек А и В на прямую а опущены перпендикуляры АС и ВД, причем АС = ВД.

Докажите, что ΔАСД = ΔВДС.

4. Задача № 2.

Дано: ΔАОВ = ΔСОД.

Доказать: ΔВОС = ΔДОА.

IV. Итоги урока.

Домашнее задание: знать доказательство первого признака равенства треугольников п. 15, решить задачи № 93, 94 и 95.