Математика 9 класс подготовка к ГИА
Решение иррациональных уравнений и уравнений, содержащих неизвестное под знаком модуля - Краткий теоретический справочник
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
К простейшим иррациональным уравнениям относятся уравнения вида ![]()
Основные способы решения иррационального уравнения.
I. Переход к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
1) По определению ![]()
2) От иррационального уравнения вида ![]() можно перейти к равносильной ему системе:
можно перейти к равносильной ему системе:
![]()
3) От иррационального уравнения вида ![]() можно перейти к одной из равносильных ему систем:
можно перейти к одной из равносильных ему систем:
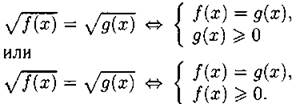
Неравенство g(х) ≥ 0 (или f(x) ≥ 0) в этих системах выражает условие, при котором уравнение можно возводить в чётную степень, отсекает посторонние решения и позволяет обходиться без проверки.
II. Введение новой переменной.
Если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины, то имеет смысл обозначить это выражение какой-нибудь новой переменной и попытаться решить уравнение сначала относительно введённой неизвестной, а затем уже найти исходную неизвестную.
Например, ![]() Обозначим
Обозначим ![]() тогда уравнение равносильно системе уравнении
тогда уравнение равносильно системе уравнении ![]()
III. Метод сведения к эквивалентным системам рациональных уравнений.
Уравнения вида ![]() где а, b, с, d — некоторые числа, часто удаётся решить при помощи введения двух вспомогательных неизвестных
где а, b, с, d — некоторые числа, часто удаётся решить при помощи введения двух вспомогательных неизвестных ![]() где у, z ≥ 0 и последующего перехода к эквивалентной системе рациональных уравнений. Полученное уравнение будет содержать две неизвестных, которые зависят одна от другой посредством старой переменной х. С помощью преобразований можно получить систему двух уравнений относительно двух неизвестных y и z.
где у, z ≥ 0 и последующего перехода к эквивалентной системе рациональных уравнений. Полученное уравнение будет содержать две неизвестных, которые зависят одна от другой посредством старой переменной х. С помощью преобразований можно получить систему двух уравнений относительно двух неизвестных y и z.
IV. Использование свойства монотонности функций.
Если уравнение имеет вид f(x) = 0, где f(x) возрастает (убывает), или f(x) = g(x), где f(x) и g(x) «встречно монотонны», то есть f(x) возрастает, а g(х) убывает или наоборот, то такое уравнение имеет не более одного корня. Если удаётся привести уравнение к такому виду и найти корень, то он и будет решением данного уравнения. Во многих случаях корень такого уравнения удобно находить подбором.