Сравнение бесконечно малых - ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Бесконечно малые величины можно сравнивать по скорости их стремления к нулю.

Если α(х) и δ(x) — две бесконечно малые и 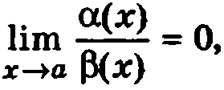то говорят, что бесконечно малая α(x) есть бесконечно малая более высокого порядка малости, чем бесконечно малая δ(x).

Если α(х) и δ(x) — две бесконечно малые и 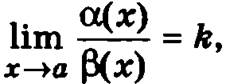где k — постоянная, то говорят, что бесконечно малые α(x) и δ(x) есть бесконечно малые одного порядка малости.

Если α(х) и δ(х) — две бесконечно малые и то говорят, что α(x) и δ(x) эквивалентные бесконечно малые α(x) ~ δ(x).

Учитывая приведенные выше пределы, можно указать следующие эквивалентные бесконечно малые при x → 0:

Теорема. Предел отношения функций равен пределу отношения их эквивалентных.

Эта теорема позволяет при вычислении пределов заменять функции их эквивалентными величинами.

Пример.

Кроме неопределенностей вида 0/0 и 1∞, которые встречались в ранее рассмотренных пределах, существуют неопределенности других видов.

Неопределенность вида ∞ - ∞

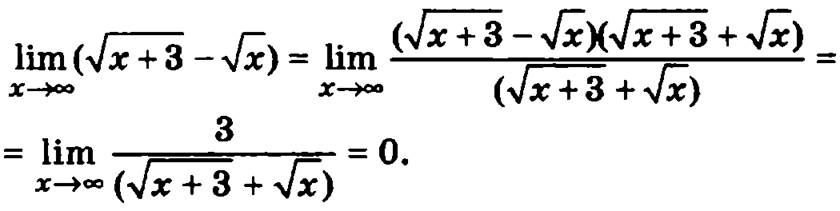
Неопределенность вида ∞/∞

Неопределенность вида ∞ ∙ 0