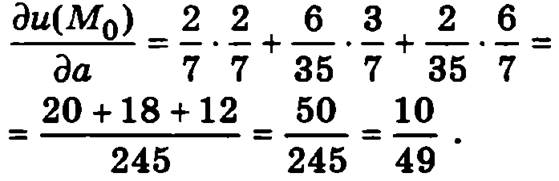Высшая математика мини-справочник для ВУЗов
Градиент функции. Производная по направлению - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть в некоторой области трехмерного пространства Q определена функция u = (х, у, z).
Определение. Градиентом функции u = (х, у, z) в точке М0(х0, y0, z0) ∈ Q называется вектор gradu(M0) с координатами 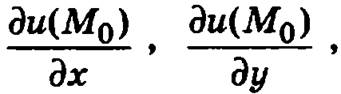
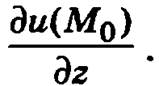
Градиент функции указывает направление наискорейшего возрастания функции.
Пример. Пусть дана функция ![]() Найдем градиент этой функции в точке М0(1, 2, 3).
Найдем градиент этой функции в точке М0(1, 2, 3).
Определим частные производные функции в этой точке:
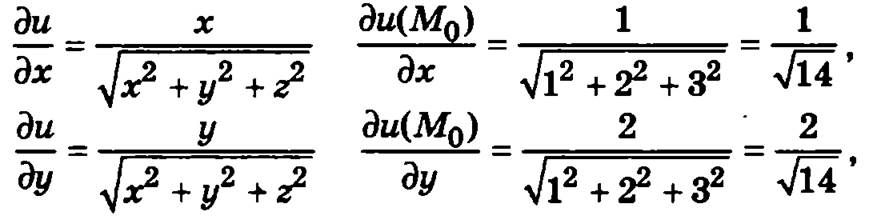
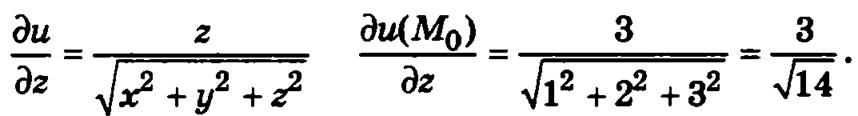
Таким образом, градиент данной функции в точке М0(1, 2, 3) равен 
Возьмем некоторую точку M0(x0, у0, z0) и проведем через нее прямую, совпадающую по направлению с вектором ![]() . Рассмотрим значение функции u = u(х, у, z) = u(М) в точке М0(х0,y0, z0) и в точке близкой к ней М1(х1, y1, z1).
. Рассмотрим значение функции u = u(х, у, z) = u(М) в точке М0(х0,y0, z0) и в точке близкой к ней М1(х1, y1, z1).
Определение. Производной функции u = u(М) в точке М0(х0, у0, z0) по направлению ![]() называется предел
называется предел  если этот предел существует.
если этот предел существует.
Если функция u = u(М) дифференцируема в точке М0(x0, y0, z0), то в этой точке существует ее производная по любому направлению, равная
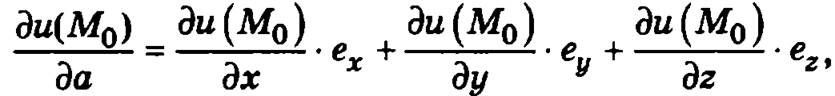
где вектор ![]() единичной длины, совпадающий по направлению с вектором
единичной длины, совпадающий по направлению с вектором ![]() .
.
Пример. Найти производную по направлению ![]() функции u = ln(х2 + у2 + z2) в точке М0(5, 3, 1).
функции u = ln(х2 + у2 + z2) в точке М0(5, 3, 1).
Вычислим частные производные функции в точке М0(5, 3, 1):
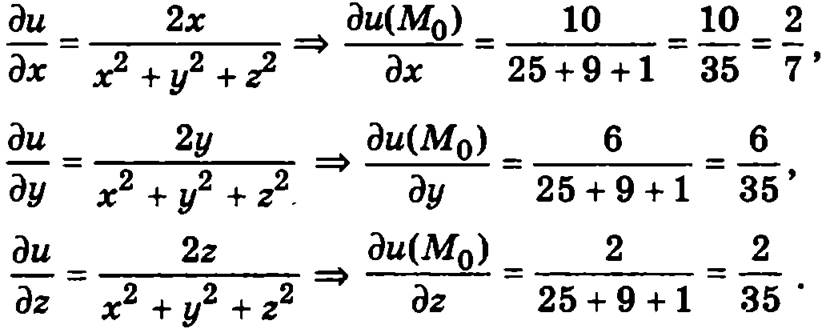
Найдем единичный вектор, совпадающий по направлению с вектором ![]() .
.
![]()
тогда
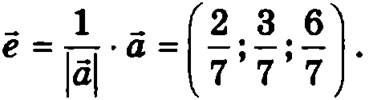
Окончательно будем иметь