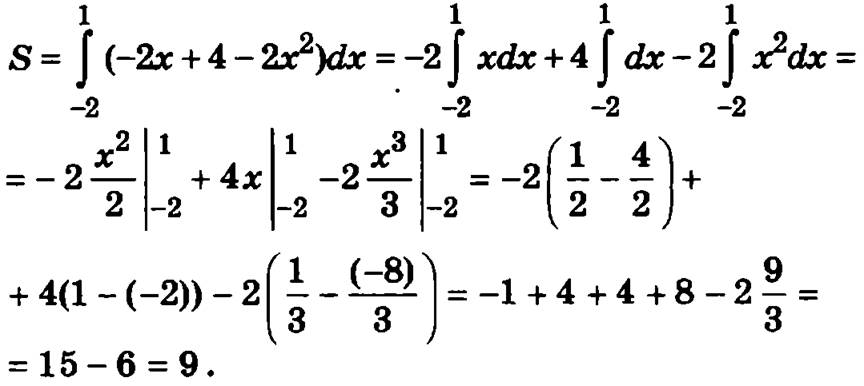Высшая математика мини-справочник для ВУЗов
Геометрический смысл определенного интеграла - ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл от функции f(x) по отрезку [а, b], на котором данная функция принимает положительные значения, численно равен площади криволинейной трапеции, ограниченной графиком f(x), осью ОХ и вертикальными прямыми х = а и х = b.
Применение определенных интегралов для вычисления площадей плоских фигур
Пусть необходимо вычислить площадь фигуры ABCD, ограниченной вертикальными прямыми х = а, х = b и кривыми линиями, которые являются графиками функций у = f(х) и у = g(x)(рис. 11).

Рис. 11
Используя определенный интеграл, площадь указанной фигуры можно выразить следующей формулой:
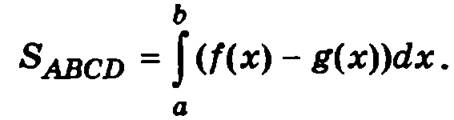
Эта формула будет справедлива и в том случае, когда вертикальные границы области отрезка АВ или CD вырождаются в точки (то есть совпадают точки А, В и точки С, D).
Пример. Вычислить площадь плоской фигуры, ограниченной линиями у = 2х2 и у = -2х + 2.
Границами данной области являются парабола у = 2х2, расположенная ветвями вверх, с вершиной в начале координат, и прямая линия у = -2х + 4. Для определения пределов интегрирования найдем точки пересечения указанных линий, решив систему уравнений
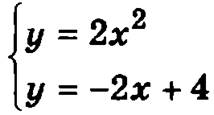
Исключив неизвестное у, получим следующее уравнение относительно неизвестного х:
у = 2х2 = -2х + 4.
Разделим обе части полученного уравнения на 2:
х2 = -х + 2.
Перенесем все члены уравнения вправо:
х2 + х - 2 = 0.
Решим это уравнение, используя известную формулу для вычисления корней квадратного уравнения:

где a, b, с — коэффициенты квадратного уравнения ах2 + bх + с = 0.
В нашем случае a = 1, b = 1, c = -2. Тогда


Взяв знак минус, получим значение для первого корня уравнения х1 = -2, взяв плюс, получим второй корень х1 = 1.
На рис. 12 представлена рассматриваемая фигура.

Рис. 12
В данном случае f(x) = -2х + 4, g(x) = 2х2, а = -2, b = 1.