Однородные дифференциальные уравнения первого порядка - ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальное уравнение первого порядка называется однородным, если оно может быть приведено к виду

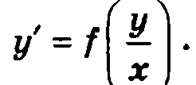
Однородные дифференциальные уравнения можно рассматривать как частный случай дифференциальных уравнений с разделяющимися переменными, к которым они могут быть сведены. Для этого вводят новую неизвестную функцию z = y/x.

Тогда у = z ∙ х , а у' = z'х + z. Подставляя приведенные соотношения в (5), получим

z'x + z = f(z) или z'x = f(z) - z.

Полученное дифференциальное уравнение является уравнением с разделяющимися переменными.

Заменим в нем z' на dz/dx: 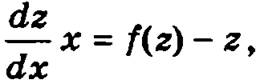а затем умножим обе его части на dx

dz ∙ x = (f(z) - z) ∙ dx.

Далее, разделим обе части уравнения на х ∙ (f(z) - z), получим

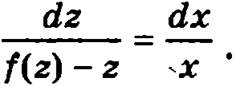
Интегрируя приведенное выше соотношение 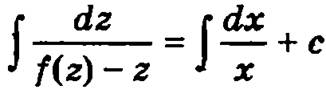и возвращаясь к старой неизвестной функции y, делая замену z = y/x, получим общее решение исходного однородного дифференциального уравнения первого порядка.

Пример. Найти частное решение дифференциального уравнения 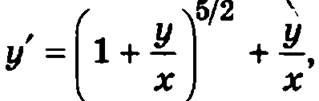удовлетворяющее начальному условию y(1) = 0.

После введения новой неизвестной функции z = y/x (у = z ∙ х, а у' = z'x + z) дифференциальное уравнение примет вид

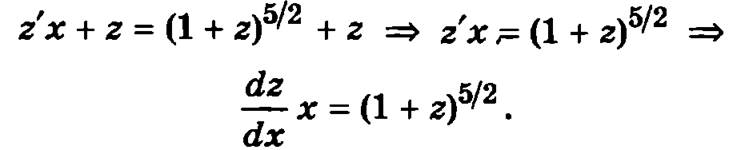
Умножая полеченное уравнение на dx

а затем деля на х (1 + z)5/2, получим

Для завершения построения общего решения проинтегрируем приведенное выше соотношение

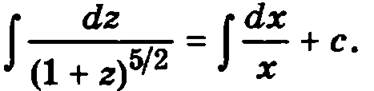
Интеграл, стоящий в правой части, является табличным

В интеграле 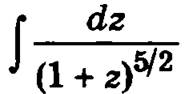сделаем замену переменной интегрирования

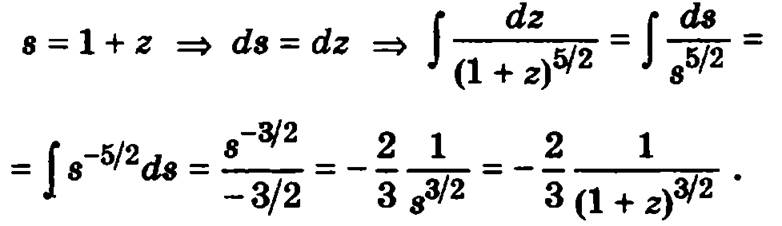
Тогда 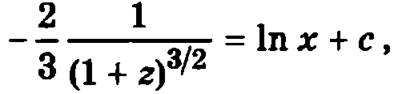а общее решение уравнение выразится в виде

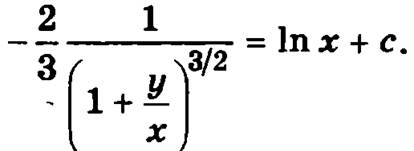
Подставляя в общее решение х = 1, у = 0 (начальное условие), получим

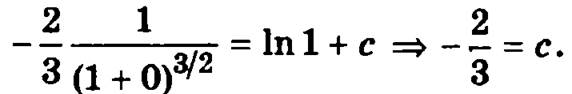
Тогда при данном значении с общее решение примет вид, соответствующий определяемому частному решению