Высшая математика мини-справочник для ВУЗов
Решение систем линейных уравнений методом матричного исчисления - ЛИНЕЙНАЯ АЛГЕБРА
Вновь рассмотрим систему линейных уравнений, у которой число неизвестных n равно числу уравнений m. Введем в рассмотрение матрицу- столбец неизвестных (матрицу, в состав которой входит лишь один столбец)

и матрицу-столбец правых частей

Тогда система линейных уравнений может быть представлена в виде ![]() где А — матрица системы.
где А — матрица системы.
Матрица А-1 называется обратной по отношению к квадратной матрице А, если справедливы соотношения А-1 ∙ А = А ∙ А-1 = Е.
Обратной к матрице А является транспонированная матрица алгебраических дополнений матрицы А, деленных на ее определитель |А|:

Из приведенного выше определения обратная матрица существует только у матриц, определитель которых не равен нулю. Такие матрицы называются невырожденными. Матрицы, определитель которых равен нулю, называются вырожденными.
Умножим систему линейных уравнений, представленную в виде ![]() слева, на матрицу А-1:
слева, на матрицу А-1:
![]()
Учитывая, что А-1 ∙ А = Е и ![]() получим
получим ![]()
То есть для получения решения системы линейных уравнений надо матрицу, обратную матрице системы, умножить слева на матрицу-столбец правых частей.
Пример. Решим изложенным выше методом систему линейных уравнений
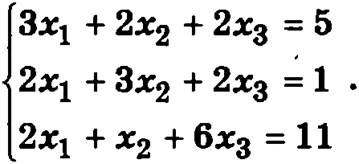
Найдем матрицу, обратную матрице данной системы уравнений
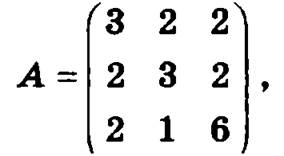
для чего вначале вычислим ее определитель, разложив его по элементам первой строки:
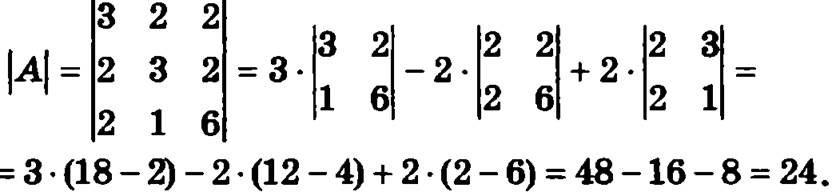
Далее вычислим алгебраические дополнения всех элементов матрицы решаемой системы уравнений:
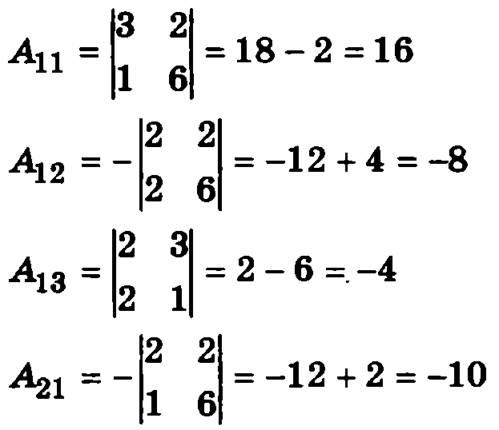
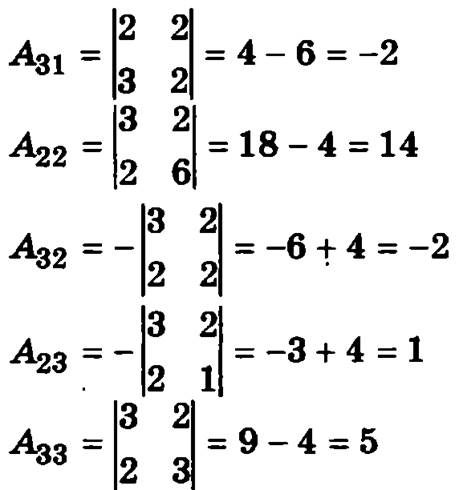
Используя вычисленные алгебраические дополнения, построим обратную матрицу
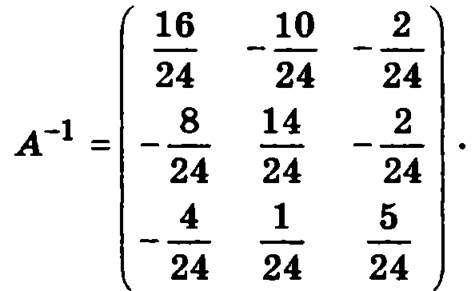
После этого определим матрицу-столбец неизвестных:

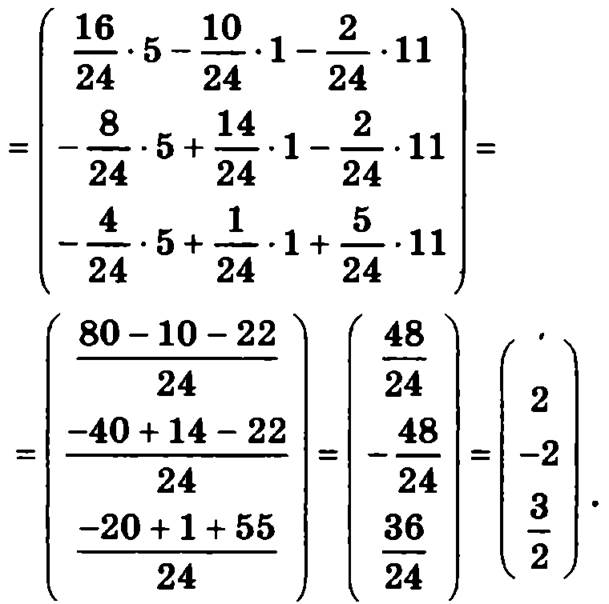
Следовательно, решением данной системы будут значения неизвестных
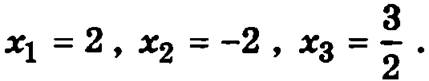
Необходимо отметить, что данный, метод может быть использован при решении систем линейных уравнений, у которых число уравнений равно числу неизвестных и определитель системы не равен нулю.