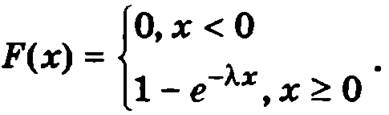Высшая математика мини-справочник для ВУЗов
Непрерывные случайные величины - ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Непрерывная случайная величина (НСВ) Х задается своей функцией распределения F(x), которая выражает для каждого х вероятность того, что случайная величина примет какое-нибудь значение, меньшее х
F(x) = Р(Х < х).
Свойства функции распределения НСВ:
1. Функция распределения НСВ F(x) является непрерывной функцией (в отличие от функции распределения ДСВ, которая является разрывной).
2. Функция распределения HCB F(x) принимает значения на отрезке [0; 1].
3. Функция распределения НСВ F(x) является неубывающей, т.е. если х2 > x1, то F(x2) > F(x1).
4. При х → +∞ F(x) → 1, а при х → -∞ F(x) → 0.
Плотностью вероятности φ(x) НСВ X называется производная от ее функции распределения F(x)
φ(x) = F’(x).
Функция φ(x) неотрицательна и

Вероятность того, что случайная величинах примет какое-либо значение внутри отрезка [x1, x2], определяется формулой

Примеры. НСВ называется распределенной по показательному закону, если она принимает только неотрицательные значения и ее плотность вероятности имеет вид

где λ > 0.
Функция распределения данной НСВ