Путешествие в историю математики - Свечников А. А. 1995
Малый счет у славян
Наши не очень далекие предки славяне, как и многие другие народы, долгое время пользовались для сохранения чисел зарубками на палочках. Один из таких древнейших памятников представлял собой кость с 55 зарубками, расположенными по пять в каждом ряду. Ученые определили, что эта кость пролежала в земле около 5000 лет и на ней, вероятно, записано число трофеев первобытного охотника.
Палочки с зарубками славяне называли бирками, и на Руси ими пользовались неграмотные люди еще в начале XX в. На палочке- бирке делали надрезы. Число надрезов указывало, например, размер долга или количество взятого зерна. Палочку раскалывали на две части, одну из которых брал должник, а другую хранил как расписку тот, кто давал в долг. При окончательном расчете обе половинки бирки складывали. Такой способ записи чисел существовал и у некоторых других народов. Так, в Англии при учете налогов на крестьян также пользовались бирками. Когда в 1834 г. было решено уничтожить долговые обязательства, то в лондонском казначействе начали сжигать огромное количество бирок. Костер был таким большим, что огонь перекинулся на само здание, и оно полностью сгорело.
В середине IX в. был создан церковнославянский алфавит, который в конце X в. стал довольно быстро распространяться на Руси. Тогда же алфавитом стали пользоваться и для записи чисел, подобно греческой алфавитной нумерации. В славянской нумерации цифры обозначали буквами с особым над ними значком — титло. Буквы от а до / в порядке их следования в алфавите обозначали единицы. Называли их в то время персты (пальцы). Числовое значение буквы определялось ее местом в порядке алфавита, например:
![]()
и т. д.
Буквы от i до n обозначали десятки, следующие буквы обозначали сотни.
В то время славяне пользовались двойной нумерацией: одну называли малый счет, а другую — великий счет. Малый счет позволял считать до 10 ООО. В самых ранних рукописях это число называли тьма, т. е. число, которое трудно представить. Числа 11, 12 и т. д. до 20 записывали двумя буквами, например:
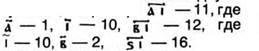
В двузначных числах на первом месте стояли единицы, а на втором — десятки. Отсюда пошли названия: одиннадцать — «один на десять», семнадцать (дцать — сокр. десять) — «семь на десять», двадцать — «два на десять» и т. д. При записи многозначных чисел титло ставили только на первом знаке. В числе 25 писали сначала ![]()
![]() , и называли эти числа в порядке записи цифр — «двадцать пять».
, и называли эти числа в порядке записи цифр — «двадцать пять».
Славянская алфавитная нумерация чисел до 800.

Числа, содержащие тысячи, славяне записывали с особым значком впереди. например:
![]() , стоящий
, стоящий
перед числом, указывал на то, что первое число означает тысячи, поэтому его надо прочитать «три тысячи семьдесят два».
Из общего порядка названий круглых десятков выделяются два числа — 40 и 90. В названиях этих чисел нет обычной для других чисел частицы дцать (двадцать, тридцать). Слово сорок (и имеющее тот же смысл сорочок) родственно слову сорочка (рубаха). Предполагают, что в древние времена на шитье мехового кафтана или шубы шла связка шкурок куницы или соболя, которую называли сорок. Подобную связку, но более дешевых шкурок, например беличьих, называли сорочком. Сороками или сорочками, т. е. наборами шкурок на один кафтан, считали количество мехов. Позже название сорок распространилось на число 40.

Слово девяносто является производным от сочетания слов девять до ста, так как от 90 до 100 есть еще девять единиц. При этом в слове девяносто звук [н] включен для облегчения произношения — вначале он отсутствовал.
Слово сто позаимствовано из латинского центум. Цент входит во многие слова, пришедшие из латинского языка, например: центурион (сотник в римских войсках), центнер, процент и др.
Упражнения и задачи
1. Какое самое большое число можно записать тремя знаками (цифрами) в десятичной системе счисления, в двоичной системе счисления?
Ответ: 999; 111.
2. На одной из египетских пирамид сохранилось число 2520, записанное иероглифами. Оно интересно тем, что делится на все однозначные числа. Проверьте!
3. Вычислите суммы пар чисел-перевертышей: 12 и 21; 123 и 321; 1234 и 4321. Заметьте свойства сумм таких чисел и, пользуясь ими, не вычисляя, найдите: 12 345 + 54 321, 123 456 + 654 321. Проверьте сложением.
Ответ: 12 345 + 54 321=66 666; 123 456 + 654 321 = 777 777.
4. Какой высоты получится столбик, если кубический дециметр разрезать на кубические сантиметры, а полученные маленькие кубики поставить один на другой?
Ответ: Высота столбика из 1000 кубиков размером 1 см2 составит 1000 см, т. е. 10 м.
5. Сколько необходимо использовать цифр, чтобы записать все двузначные числа?
Ответ: 180 (90 • 2).