Путешествие в историю математики - Свечников А. А. 1995

Фалес из Милета

Одним из семи мудрецов древно­сти считают Фалеса Милетского (ок. 624 — 548 до н. э.). Будущий ученый родился в городе Милете, находившемся в западной части побережья Малой Азии. Фалес предсказал солнечное затмение 585 г. до н. э. Он сделал немало важных открытий в различных об­ластях науки. Его считают отцом греческой математики.

Фалес Милетский.

Гравюра XVII в.

Однажды Фалес отправился по торговым делам в Египет. Там он пробыл несколько лет и настоль­ко глубоко изучил достижения египетских жрецов, что вскоре превзошел их в знаниях.

Рассказывают, что фараон по­желал узнать высоту пирамиды, но никто не мог ее определить. Фалес легко справился с этой за­дачей. Он выбрал день и час, ког­да его собственная тень стала равной его росту. Измерив тень, которую отбрасывала пирамида, он установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его прибли­женные были изумлены, как точ­но, быстро, без специальных при­боров северный пришелец решил трудную задачу.

Измерение высоты пирамиды по ее тени.

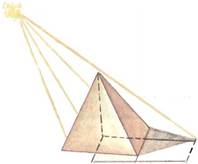
Однако, прежде чем сделать такое простое измерение, Фалес должен был открыть и доказать, что углы при основании равнобед­ренного треугольника равны и что против равных углов в треуголь­нике лежат равные стороны, а также, что сумма углов любого треугольника равна двум прямым углам. Фалес доказал также тео­рему о равенстве двух треуголь­ников, если сторона и два приле­жащих к ней угла одного треуголь­ника соответственно равны сто­роне и двум прилежащим к ней углам другого треугольника. На основании этой теоремы Фалес Милетский определил, как изме­рить расстояние от конкретного места на берегу до корабля, нахо­дящегося недалеко в море.

Теорема Фалеса о равенстве двух треугольников.

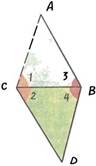
Угол (прямой), вписанный в полуокружность.

Предполагают, что ученый рас­суждал так. Чтобы определить расстояние от точки В до точки А, надо провести произвольную ли­нию ВС и измерить угол 1 (ВСА), затем отложить у той же точки С равный ему угол 2. Измерить угол 3 и у его вершины В отложить рав­ный ему угол 4. Так как получив­шиеся треугольники АВС и BCD равны, то их стороны АВ и BD то­же равны. Измерив BD, находили искомое расстояние АВ. Равен­ство треугольников АВС и BCD следует из того, что эти треуголь­ники имеют общую сторону ВС и по два равных. прилежащих к ней угла

Кроме указанных теорем Фале­су приписывают доказательство следующих теорем: диаметр де­лит круг пополам; любой из углов, вписанных в полуокружность, — прямой; вертикальные углы рав­ны.

Некоторые из этих утвержде­ний были известны вавилонянам и египтянам и до Фалеса, но до не­го их не доказывали, а установили практическими измерениями на примере частных случаев. Фалес же указанные положения доказы­вал и только после этого приме­нял их на практике. Доказатель­ство позволяло ему утверждать, что та или иная теорема справед­лива для взятых в ней фигур во всех случаях. Введя в практику доказательства теорем, Фалес заложил основы создания геоме­трии как науки. После него ка­ждое открытие в геометрии древ­ние ученые стремились обосно­вать доказательством и только после этого считали его истин­ным.

Фалес был знаком с вавилон­ской астрономией и сделал ряд важных открытий в этой науке. Он настолько увлекался наблюдени­ями за движением небесных све­тил, что иногда не замечал окру­жающих предметов. Существует предание, что однажды, наблюдая звездное небо, Фалес на­столько был поглощен этим заня­тием, что упал в глубокий ров, а сопровождавшая его женщина воскликнула: «Как можешь ты знать, что делается на небе, ког­да не видишь того, что делается у тебя под ногами!»

Как философ Фалес утверж­дал, что все явления в мире не случайны, а закономерны; все, что существует, развилось из еди­ной первоматерии — воды. Он го­ворил: «Праматерия не исчезает, меняются только формы суще­ствующего».