Математика 5 класс - Поурочные разработки
Задачи на движение навстречу и в противоположных направлениях - Задачи на движение - Действия с натуральными числами
Цели: познакомить с терминами «скорость удаления», «скорость сближения»; формировать умение решать задачи данного типа.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите:
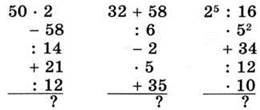
2. Какой цифрой оканчивается куб числа: 925; 113; 482; 527?
III. Актуализация знаний.
1. Автомобиль проехал 120 км за 3 ч. С какой скоростью ехал автомобиль?
2. Автомобиль едет со скоростью 60 км/ч. Какое расстояние проедет он за 4 ч?
3. Автомобиль едет со скоростью 50 км/ч. За какое время он проедет 100 км?
Текст задачи и решение целесообразно записать в тетрадях, чтобы в дальнейшем в случае затруднения учащиеся могли к ним обратиться как к опорным ситуациям.
4. Что означает термин «скорость»? Приведите примеры скоростей.
IV. Изучение нового материала.
1. У, № 340.
а) 70 + 90 = 160 (км/ч) — скорость удаления (рис. 61).
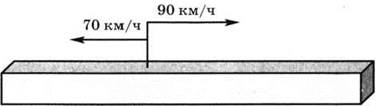
Рис. 61
б) 70 + 90 = 160 (км/ч) — скорость сближения (рис. 62).

Рис. 62
При необходимости эту ситуацию можно разыграть.
2. У, № 341 (устно).
3. Рассмотрите решения задач 1 и 2 из п. 3.5 учебника.
V. Формирование умений и навыков.
1. Анализ и решение задачи № 342 из учебника на движение тел в противоположных направлениях (рис. 63).
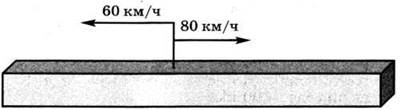
Рис. 63
Способ 1.
1) Сколько километров за 2 ч проедет первый автомобиль?
2) Сколько километров за 2 ч проедет второй автомобиль?
3) Сколько километров за 2 ч проедут оба автомобиля вместе?
4) Какое расстояние будет между ними через 2 ч?
1) 60 · 2 = 120 (км);.
2) 80 · 2 = 160 (км);
3) 120 + 160 = 280 (км).
Способ 2.
1) На сколько километров изменится расстояние между двумя автомобилями за час? 60 + 80 = 140 (км).
2) Найдем, на каком расстоянии будут автомобили друг от друга через 2 ч.
140 · 2 = 280 (км).
3) Какое расстояние будет между ними через 3 ч? Вывод. Если известны скорости тел, движущихся в противоположных направлениях, то можно найти скорость удаления. Она будет равна сумме скоростей данных тел.
2. Анализ и решение задачи № 344 из учебника на движение навстречу друг другу (рис. 64).

Рис. 64
Способ 1.
1) Сколько километров проедет первый автомобиль за 2 ч?
2) Сколько километров проедет второй автомобиль за 2 ч?
3) Сколько километров проедут автомобили вместе за 2 ч?
4) Какое расстояние будет между ними через 2 ч?
1) 60 · 2 = 120 (км).
2) 80 · 2 = 160 (км);
3) 120 + 160 = 280 (км);.
4) 500 - 280 = 220 (км).
Способ 2.
1) 60 + 80 = 140 (км/ч) — скорость сближения;
2) 140 · 2 = 280 (км) — проедут автомобили за 2 ч.
3) 500 - 280 = 220 (км) — расстояние между автомобилями через 2 ч.
Какое расстояние будет между ними через 3 ч?
Вывод. Если известны скорости тел, движущихся навстречу друг другу, то можно найти скорость их сближения. Она будет равна сумме скоростей данных тел.
VI. Закрепление.
У, № 343, 345 (самостоятельно, по вариантам).
VII. Итоги урока.
1. Что можно найти, если известны скорости тел, движущихся в противоположных направлениях?
2. Что можно найти, если известны скорости тел, движущихся навстречу друг другу?
3. Со станции одновременно отправились два поезда в разных направлениях. Скорость одного 40 км/ч, а другого 60 км/ч. Составьте вопросы к задаче и ответьте на них.
VIII. Домашнее задание.
У, № 346, 347, 276 (в, г).