Решение задач на уравнивание - Задачи на уравнивание - Использование свойств действий при вычислениях

Цель: формировать умение решать задачи на уравнивание.

Ход урока

I . Организационный момент.

II. Устная работа.

Лесенка. Класс делится на три команды. Члены команд выходят по одному к доске и выполняют только одно действие из своей лесенки (рис. 86). Каждый учащийся может исправить (если есть) ошибку предыдущего и сделать одно следующее действие. Выигрывает та команда, которая первой с верным ответом доберется до последней ступеньки.

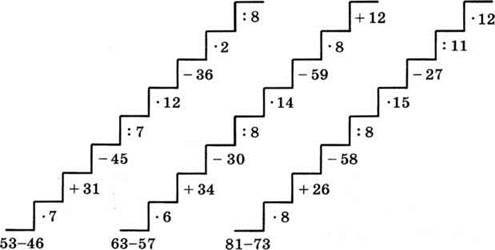
Рис. 86

III. Формирование умений и навыков.

1. У, № 448 (а).

Способ 1. Пусть оба числа равны меньшему из них, тогда их сумма будет 432 - 18 = 414. 414 : 2 = 207 — меньшее число, а 207 + 18 = 225 — большее число (см. рис. 87).

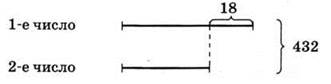
Рис. 87

Способ 2. Пусть оба числа равны большему из них, тогда сумма будет 432 + 18 = 450. 450 : 2 = 225 — большее число, а 225 - 18 = 207 — меньшее число.

2. У, № 450. Сделайте рисунок (см. рис. 88).

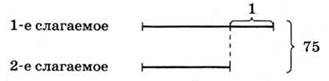
Рис. 88

3. У, № 453. а) На сколько отличаются друг от друга последовательные натуральные числа? Сделайте рисунок (см. рис. 89).

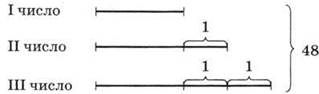
Рис. 89

Будем считать, что слагаемые равны меньшему из чисел, тогда их сумма будет 48 - 3 = 45; 45 : 3 = 15 — меньшее число, а два других — это 15 + 1 = 16 и 16 + 1 = 17. Проверка: 15, 16, 17 — это последовательные натуральные числа и 15 + 16 + 17 = 48.

4. У, № 455. Если бы отцу было столько же лет, сколько матери, то сумма возрастов была бы 103 - 5 = 98. Примем возраст матери за 20 частей. Сколько частей приходится на возраст сына? Сколько частей приходится на возраст дочери?

20 + 20 + 5 + 4 = 49 — частей приходится на суммарный возраст;

98 : 49 = 2 (года) — 1 часть;

2 · 20 = 40 (лет) — матери;

40 + 5 = 45 (лет) — отцу;

2 · 5 = 10 (лет) — сыну;

2 · 4 = 8 (лет) — дочери.

Физкультминутка «Зрительная гимнастика»

5. Проверочная работа. ДМ, П-17. Дополнительно: У, № 447 (а, б — по вариантам).

IV. Итоги урока.

1. В чем состоит метод решения задач на уравнивание?

2. Любую ли задачу можно решить с помощью уравнивания?

3. Какие задачи можно решать с помощью уравнивания?

V. Домашнее задание.

У, № 448 (б), 451, 290 (г).