Сложение чисел с помощью координатной прямой - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ - РАЦИОНАЛЬНЫЕ ЧИСЛА

Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.

Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек числовой оси. При изучении данной темы целенаправленно отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.

СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ (2 ч)

Урок 107. Сложение чисел с помощью координатной прямой

Цели: отрабатывать умение складывать положительные и отрицательные числа с помощью координатной прямой; развивать умение объективно оценивать труд своих товарищей.

Информация для учителя

Обратить внимание учащихся, что сумма двух чисел не всегда больше каждого слагаемого.

Ход урока

I. Организационный момент

Если хочешь строить мост.

Наблюдать движенье звезд,

Управлять машиной в поле

Иль вести машину ввысь,

Хорошо работай в школе,

Добросовестно учись.

(M. Бозаковский)

II. Анализ контрольной работы

1. Ознакомить учащихся с результатами контрольной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

III. Устный счет

1. Какое целое число стоит между числами:

—1 и 1; —7,3 и —6,7; —0,2 и 0; —3,6 и —2,9; -2 и 0; -0,5 и -0,2; —1,4 и 0; -2,3 и —1,3?

2. На день 2 лошадям выдают 10 кг овса. Сколько килограммов овса нужно 8 лошадям на 4 дня?

3. Что меньше: 3 тонны или 210 центнеров?

4. Изобретатели внесли три предложения по экономии электроэнергии, необходимой для работы мастерской. Одно из этих предложений дает 30% экономии, другое 50%, а третье 20%. Решено было осуществить все три предложения. Можно подумать, что мастерской вообще не нужна электроэнергия. Так ли это? (Расход энергии составит 28% первоначального.)

5. В неверном равенстве 101 = 10 2 — 1 передвиньте одну цифру так, чтобы оно стало верным. (101 = 102 — 1.)

6. Решите ребус:

ВИ 3 НА (Витрина.)

100 Л (Стол.)

ПРО 100 Р (Простор.)

IV. Индивидуальная работа

1 карточка

Составить выражение к условию задачи.

1) Скорость течения реки с км/ч, собственная скорость лодки b км/ч. Какова скорость лодки против течения и по течению?

2) Скорость катера по течению реки равна а км/ч, а скорость течения реки - b км/ч. Найдите скорость катера против течения.

3) Скорость теплохода по течению реки равна d км/ч, а против течения — с км/ч. Какова собственная скорость теплохода?

(Ответы: 1) b — с; b + с; 2) а — 2b; 3) (d + с) : 2.)

2 карточка (для более подготовленных учащихся)

Составить выражение к условию задачи.

1) Скорость парохода по течению реки равна а км/ч, а скорость плота на этой реке — b км/ч. Какое расстояние проплывет пароход за 5 ч, двигаясь по озеру?

2) Скорость течения реки, равная с км/ч, составляет 20% собственной скорости лодки. Какова скорость лодки против течения?

3) Скорость теплохода по течению реки равна d км/ч, а против течения - на 20% меньше. Какова собственная скорость теплохода?

(Ответы: 1) 5(а — b); 2) с : 0,2 — с = 4с; 3) (d + 0,8d) : 2 = 0,9d.)

V. Сообщение темы урока

— Сегодня на уроке мы будем учиться складывать положительные и отрицательные числа с помощью координатной прямой.

VI. Изучение нового материала

1. Подготовительная работа.

— Каким числом выражается увеличение любой величины? (Положительным.)

— А уменьшение? (Отрицательным.)

— Как называются числа при сложении? (1-е слагаемое, 2-е слагаемое и сумма.)

2. Работа с учебником. Чтение и разбор параграфа по отдельным абзацам.

— Откройте учебник на стр. 171. Прочитайте 1 абзац § 31.

— Приведите свои примеры увеличения любой величины. Запишите данную сумму на доске.

— Сравните результат сложения с каждым слагаемым. (Результат сложения, то есть сумма, больше каждого слагаемого.)

— Прочитайте 1 абзац на стр. 172.

— Приведите свои примеры уменьшения любой величины. Запишите данную сумму на доске.

— Сравните результат сложения с каждым слагаемым. (Результат сложения, то есть сумма, меньше первого слагаемого, но больше второго.)

— Почему? (Второе слагаемое выражено отрицательным числом, а сумма — положительным числом, а по правилу сравнения чисел любое положительное число больше любого отрицательного.)

— Сделайте вывод, что происходит с первым слагаемым, когда прибавляют положительное число или отрицательное число. (Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.)

— Прибавить к числу а число b — значит изменить число а на b единиц.

— Рассмотрите рис. 74, где показано, как с помощью координатной прямой выполнено сложение чисел.

— Куда перемещается точка на координатной прямой, когда прибавляют положительное число? (На 3 единицы вправо.)

— Отрицательное число? (На 3 единицы влево.)

— Рассмотрите самостоятельно примеры 3 и 4 в учебнике на стр. 173. Какие выводы делают авторы учебника из рассмотренных примеров? (Сумма двух противоположных чисел равна нулю. От прибавления нуля число не изменяется.)

— Запишите эти выводы в тетрадь с помощью букв:

а + (—а) = 0; а + 0 = 0 + а = а.

— Приведите свои примеры, подтверждающие данные свойства сложения. (Записать на доске.)

VII. Закрепление изученного материала

1. Прочитайте текст в учебнике на стр. 173 под рубрикой «Говори правильно».

— Прочитайте двумя способами сумму двух чисел, записанную на доске.

2. Найдите с помощью координатной прямой сумму чисел (с подробным комментированием на доске и в тетрадях):

а) —5 и 2; 4 и —6;

б) —3 и —2; —1,5 и —3,5;

в) —4 и 4; 2 и —2;

г) 0 и 4; - 3 и 0.

3. Найдите с помощью координатной прямой значение выражения (с подробным комментированием на доске и в тетрадях):

а) (-3 + 2) + (-6);

б) -3 + (-2 + 6);

в) (-5,5 + 2,5) + 6.

VIII. Физкультминутка

IX. Работа над задачей

№ 1033 стр. 175 (самостоятельно, устная проверка).

— Прочитайте задачу. Что известно? Что надо узнать?

— К какому виду задач можно отнести эту задачу? (Задача на нахождение числа по его дроби.)

— Расскажите, как найти число по данному значению его процентов. Решите задачу самостоятельно.

Решение:

1) 78% = 0,78.

2) 156 : 0,76 = 15 600 : 76 = 200 (в.).

(Ответ: 200 выстрелов.)

X. Повторение изученного материала

1. № 1027 стр. 174 (самостоятельно, самопроверка).

— Что называют координатой точки на прямой?

— Обратите внимание на единичный отрезок.

(Ответ: )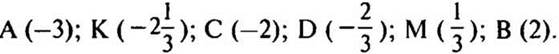

2. № 1029 стр. 174 (самостоятельно, устная проверка).

— Ответ обоснуйте. (50 — отрицательных чисел, 50 — положительных да еще 1 число — нуль.)

Решение:

50 + 1 + 50 = 101 (чисел)

(Ответ: 101 число.)

3. № 1032 стр. 175 (самостоятельно, взаимопроверка).

— Как сравнить два отрицательных числа?

Решение:

XI. Подведение итогов урока

— Что значит прибавить к числу а число 6?

— Чему равна сумма противоположных чисел? Запишите вывод в виде равенства, содержащего букву.

Домашнее задание

Прочитать текст в учебнике на стр. 173 под рубрикой «Говори правильно».

№ 1039 (а—г), 1040 стр. 175, № 1042 (а) стр. 176, продолжить работу над составлением словарика математических терминов.