Раскрытие скобок - РЕШЕНИЕ УРАВНЕНИЙ - РАЦИОНАЛЬНЫЕ ЧИСЛА

Основная цель - подготовить учащихся к выполнению преобразований выражений, решению уравнений.

Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.

Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одним неизвестным.

РАСКРЫТИЕ СКОБОК (3 ч)

Урок 130. Раскрытие скобок

Цели: ввести понятие раскрытия скобок; ознакомить с правилом раскрытия скобок; отрабатывать умения решать уравнения; развивать логическое мышление.

Информация для учителя

Учащиеся должны постоянно проговаривать правила раскрытия скобок при упрощении выражений.

Ход урока

I. Организационный момент и анализ контрольной работы

1. Познакомить учащихся с результатами контрольной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

II. Устный счет

1. Решите уравнения:

1) (х - 5)(х + 7) = 0;

2) (х - 2)(х - 6) = 0;

3) (х + 1)(х + 4) = 0;

4) (х + 3)(х - 8) = 0.

2. При каких значениях а и b верно равенство:

1) а + b = b;

2) а - b = b;

3) а + b = а;

4) а — b = а;

5) b — b = 0;

6) а + а = 0;

7) а + b = 0;

8) а — b = —b.

3. «Сколько лет твоему отцу?» — спросил Колю товарищ.

Аты посчитай сам: число его лет на 39 больше, чем наименьшее из натуральных чисел. Сколько лет Колиному отцу?

4. Разделите сто на половину. (100 : 0,5 = 200.)

5. Сосчитайте количество треугольников на чертеже.

III. Индивидуальная работа

1 карточка

1. Выполнить действие:

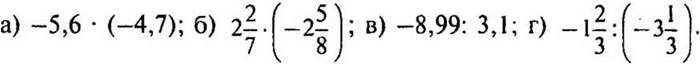
2. Выразить числа 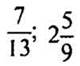в виде приближенного значения десятичной дроби до тысячных.

3. Найти значение выражения: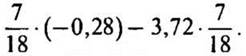

4. Найти корни уравнения: (13х — 39)(5,7у — 1,14) = 0.

2 карточка

1. Выполнить действие:

2. Выразить числа 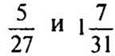в виде приближенного значения десятичной дроби до тысячных.

3. Найти значение выражения:

4. Найти корни уравнения: (17х — 68)(3,7у — 0,74) = 0

IV. Сообщение темы урока

— Тема нашего урока «Раскрытие скобок». Что это такое, вы мне объясните в конце урока.

V. Изучение нового материала

1. Подготовительная работа.

— Вспомните, как к числу прибавить сумму двух чисел и разность двух чисел.

— Запишите это свойство с помощью букв.

— Запишите в буквенном виде свойство вычитания из числа суммы и из числа разности.

2. Работа над новой темой.

1. Преобразование выражений, содержащих скобки, таким образом, что их можно записать без скобок, называют раскрытием скобок.

— Правила раскрытия скобок основываются на свойствах сложения и вычитания, которые мы с вами сейчас вспомнили.

3. Работа с учебником.

а) Рассмотрите пример 1 на стр. 214.

— Прочитайте первое правило раскрытия скобок.

— Найдите значение выражения:

-6,23 + (6,23 - 8,95) = -6,23 + 6,23 - 8,95 = 0 - 8,95 = 8,95

— На чем основано сложение чисел —6,23 и 6,23? (На свойстве сложения противоположных чисел.)

— Чему равна их сумма? (0.)

б) Что обозначает запись —а? (Число, противоположное числу а.)

— А запись — (—а)? (Число, противоположное числу —а.)

— Чему это равно? (а.)

— (—а) = а.

в) Найдите значение выражения: — (—8 + 5.).

1 способ

— (—8 + 5) = — (—3) = 3.

— Сначала мы сложили числа — 8 и 5, затем нашли число, противоположное числу —3.

2 способ

— (—8 + 5) = 8 — 5 = 3.

— Сначала найдем числа, противоположные данным слагаемым (т.е. мы изменим их знаки), а потом сложим эти числа.

Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.

— (а + Ь) = —а — b.

г) Рассмотрите пример 2 на стр. 215.

— Прочитайте второе правило раскрытия скобок.

— Вот как эти правила звучат в стихотворной форме:

Перед скобкой плюс стоит

Он о том и говорит,

Что ты скобки опускай,

Да все числа выпускай.

Перед скобкой минус строгий

Загородит нам дорогу.

Чтобы скобки убирать,

Надо знаки поменять.

— (—2а +3b) + (—4с + d) = 2а — Зb — 4с + d.

Знак минус — очень коварный, это «сторож у ворот» (скобок) и выпустит только тогда, когда все члены поменяют «паспорта» (знаки).

Знак минус — кирпич, дорожный знак «Въезд воспрещен».

VI. Физкультминутка

VII. Закрепление изученного материала

1. № 1234 стр. 216 (у доски и в тетрадях).

— Как раскрыть скобки, перед которыми стоит знак «+»?

Решение:

а) 3,4 + (2,6 + 8,3) = 3,4 + 2,6 + 8,3 = 14,3;

б) 4,57 + (2,6 - 4,57) = 4,57 + 2,6 - 4,57 = 2,6;

в) m + (n — k) = m + n — k;

г) с + (-а + b) = с - а + b.

2. № 1235 стр. 216 (у доски и в тетрадях).

— Как записать сумму, противоположную сумме нескольких слагаемых?

Решение:

а) - (-5,75 + 3,24) = 5,75 - 3,24 = 2,51;

б) - (6,38 - 2,47) = -6,38 + 2,47 = -3,91;

в)

3. № 1240 стр. 217 (первые два выражения разобрать подробно, затем самостоятельное последующей проверкой).

— Что значит найти разность двух выражений?

— Как называются числа при вычитании? (Уменьшаемое, вычитаемое и разность.)

— Назовите уменьшаемое, вычитаемое и разность в каждом случае.

— Как раскрыть скобки, перед которыми стоит знак «—»?

Решение:

VIII. Самостоятельная работа

Вариант I

Раскройте скобки:

Вариант II

Раскройте скобки:

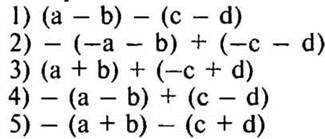
Воспользуйтесь помощью учителя или сильного ученика — консультанта.

IX. Повторение изученного материала

№ 1245 (а) стр. 218 (самостоятельно, самопроверка с образцом на доске).

— Расположите ответы в порядке возрастания.

— Не выполняя вычислений, найдите, при каком значении x выражение будет иметь наибольшее значение. (Наибольшее значение выражения будет при х = —19, так как чем меньше мы отнимаем от одного и того же числа, тем больше остается.)

Решение:

157 - х

при х = 68, 157 - 68 = 89;

при х = -19, 157 - (-19) = 157 + 19 = 176;

при х = 0,17, 157 - 0,17 = 156,83;

при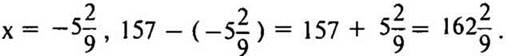

(Ответ: )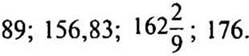

Наибольшее значение 176.

X. Подведение итогов урока

— Тема нашего урока была «Раскрытие скобок».

— Что значит раскрыть скобки?

— Расскажите, как раскрывают скобки, перед которыми стоит знак «+»?

— Расскажите, как раскрывают скобки, перед которыми стоит знак «—»?

— Как можно найти значение выражения, противоположное сумме нескольких чисел?

Домашнее задание

№ 1254 (а, б) стр. 219; № 1255 (а, б), 1256 (а, б), 1258 (а); № 1259 (а) стр. 220.