Контрольная работа № 13 - РЕШЕНИЕ УРАВНЕНИЙ - РАЦИОНАЛЬНЫЕ ЧИСЛА

Цель: контроль знаний, умений и навыков по теме «Решение уравнений».

Ход урока

I. Организационный момент

II. Выполнение работы

Вариант I

1. Решите уравнение: 0,6 (х + 7) = 0,5 (х — 3) + 6,8.

2. На первой стоянке в 4 раза меньше автомашин, чем на второй. После того как на первую приехали 35 автомашин, а со второй уехали 25 автомашин, автомашин на стоянках стало поровну. Сколько автомашин было на каждой стоянке первоначально?

3. Сумма двух чисел равна 48. Найдите эти числа, если 40% одного из них равны 2/3 другого.

4. При каких значениях х выражения 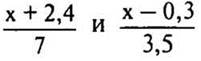будут равны?

5. Найдите два корня уравнения |-0,63| : |х| = |-0,91|.

Вариант II

1. Решите уравнение: 0,3 (х — 2) = 0,6 + 0,2 (х + 4).

2. Во второй корзине было в 3 раза больше огурцов, чем в первой. Когда в первую корзину добавили 25 кг огурцов, а из второй взяли 15 кг огурцов, то в обеих корзинах огурцов стало поровну. Сколько килограммов огурцов было в каждой корзине?

3. Разность двух чисел 33. Найдите эти числа, если 30% большего из них равны 2/3 меньшего.

4. При каких значениях у выражения 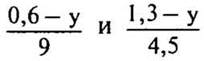будут равны?

5. Найдите два корня уравнения |-0,7| · |y| = |0,42|.

Вариант III

1. Решите уравнение: 0,5 (х — 3) = 0,6 (4 + х) — 2,6.

2. В первом букете было в 4 раза меньше роз, чем во втором. Когда к первому букету добавили 15 роз, а ко второму 3 розы, то в обоих букетах роз стало поровну. Сколько роз было в каждом букете первоначально?

3. Разность двух чисел равна 5. Найдите эти числа, если 2/9 меньшего из них равны 20% большего.

4. При каких значениях х выражения 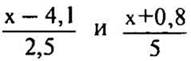будут равны?

5. Найдите два корня уравнения: |-0,56| : |у| = |0,8|.

Вариант IV

1. Решите уравнение: 0,7 + 0,3 (х + 2) = 0,4 (х — 3).

2. В первой корзине было в 3 раза больше ягод, чем во второй. Когда из первой корзины взяли 8 кг ягод, а во вторую добавили 14 кг ягод, то в корзинах ягод стало поровну. Сколько килограммов ягод было в каждой корзине первоначально?

3. Сумма двух чисел равна 138. Найдите эти числа, если 2/9 одного из них равны 80% другого.

4. При каких значениях у выражения 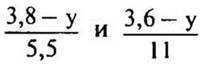будут равны?

5. Найдите два корня уравнения: |у| · |-0,9| = |-0,72|.

Творческое домашнее задание (по желанию)

Составить и решить сказочную задачу с помощью уравнения.