Поурочные разработки по Математике 6 класс

Приведение дробей к общему знаменателю - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ - ОБЫКНОВЕННЫЕ ДРОБИ

Информация для учителя

Обратить внимание учеников на разный смысл выражений: «общий знаменатель дробей», «наименьший общий знаменатель дробей (Н0З)».

Чтобы привести дробь к новому знаменателю, надо:

1) разделить новый знаменатель на знаменатель данной дроби, в результате получится число, которое является дополнительным множителем;

2) умножить числитель и знаменатель данной дроби на дополнительный множитель.

Чтобы найти наименьший общий знаменатель дробей, надо:

1) выяснить, не делится ли знаменатель одной дроби на знаменатель другой дроби. Если да, то больший знаменатель и будет НОЗ этих дробей;

2) выяснить, не являются ли знаменатели данных дробей взаимно простыми числами. Если да, то произведение этих знаменателей и будет НОЗ этих дробей;

3) если не выполняется ни 1, ни 2 пункт, то надо найти наименьшее общее кратное этих знаменателей. Это число и будет НОЗ этих дробей.

Чтобы привести дроби к наименьшему общему знаменателю, надо:

1) найти НОК знаменателей этих дробей. Оно и будет НОЗ;

2) найти дополнительный множитель для каждой дроби;

3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Урок 26. Приведение дробей к общему знаменателю

Цели: ввести понятие дополнительного множителя; отрабатывать умения приводить дроби к новому знаменателю и находить дополнительный множитель; закрепить знание основного свойства дроби и умение сокращать дроби; развивать математическую речь.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

1. Ознакомить учащихся с результатами самостоятельной работы.

2. Решить задания, в которых допущено наибольшее количество ошибок.

III. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 9 и 12; 12 и 16; 15 и 25; 3 и 4; 6 и 18; 4 и 15; 12 и 5; 6 и 20; 3 и 7.

2. Чему равен наибольший общий делитель двух чисел, если наименьшее общее кратное этих чисел равно их произведению? (1, так как числа взаимно простые.)

3. Восстановите запись:

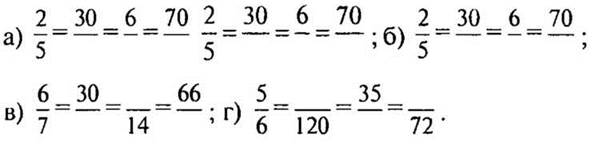
4. Объясните, почему несократимы дроби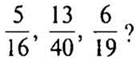

5. На столе лежало 4 яблока, одно разрезали пополам. Сколько стало яблок? (4.)

6. Из двух пунктов, находящихся на расстоянии 144 км, навстречу друг другу выехали машина и велосипедист. Скорость машины 60 км/ч, скорость велосипедиста 12 км/ч. Через какое время они встретятся? (2 ч.)

IV. Индивидуальная работа

1 карточка

1. Сократите дроби: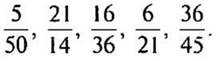

2. Сократите: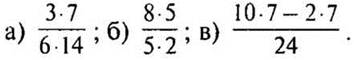

2 карточка (для сильных учащихся)

1. Сократите дроби: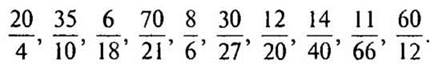

2. Сократите: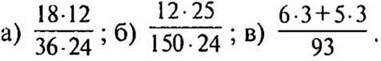

V. Сообщение темы урока

— Сегодня на уроке мы узнаем, что такое дополнительный множитель дробей, и будем приводить дроби к новому знаменателю.

VI. Изучение нового материала

1. Подготовительная работа.

№ 286 стр. 47 (устно).

(Ответ: 2, 6, 3, 8, 4.)

— Умножьте числитель и знаменатель дроби на 6: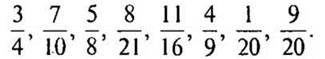

— Какая дробь получилась в результате умножения? (В результате получается дробь, равная данной, числитель и знаменатель которой кратны прежней.)

2. Работа над новой темой.

— Дана дробь 3/4. Умножьте числитель и знаменатель дроби на 2. Какая дробь получилась? (6/8.)

— Что можно сказать о дробях 3/4 и 6/8? (3/4 = 6/8.)

— В таком случае говорят, что дробь - привели к новому знаменателю 8.

— К какому новому знаменателю можно привести данную дробь? (Дробь можно привести к любому знаменателю, кратному знаменателю данной дроби.)

Определение. Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.

VII. Закрепление изученного материала

1. № 275 стр. 45 (у доски и в тетрадях с подробным комментированием).

— Что нужно сначала найти, чтобы привести дроби к новому знаменателю? (Дополнительный множитель.)

Решение:

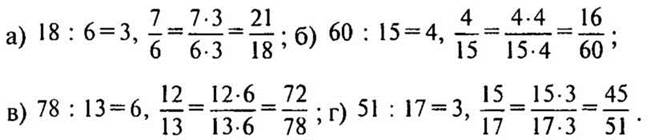
— Изменилась ли дробь после ее приведения к новому знаменателю? (Мы получили дробь, равную данной.)

— Что можете сказать о дробях 7/6 и 21/18? (Это различные записи одного и того же числа.)

2. № 276 стр. 45 (с комментированием у доски и в тетрадях).

Решение:

а) 60 : 4 · 3 = 45 мин,

60 : 4 = 15 - дополнительный множитель,

60 : 15 · 7 = 28 мин,

60 : 15 = 4 — дополнительный множитель,

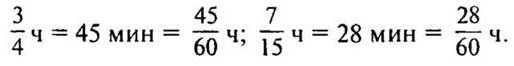
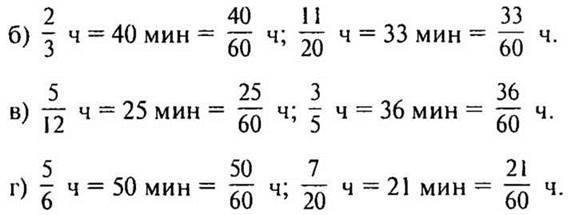
— Что интересного заметили? (Числитель новой дроби равен количеству минут.)

VIII. Физкультминутка

IX. Работа над задачей

№ 292 стр. 47 (после подробного разбора самостоятельно можно предложить решить любым способом).

— Прочитайте задачу.

— Что известно? Что надо узнать?

— Что можно узнать 1 действием? (Скорость сближения.)

— Как найти расстояние, зная скорость и время? (Скорость умножить на время.)

— Можно ли вторым действием найти расстояние? (Нет.)

— Почему? (Скорость и время выражаются разными единицами измерения.)

— В чем надо выразить 15 мин? (В секундах.)

— Сколько секунд в 1 мин? (60 с.)

— Сколько секунд в 15 мин? (15 умножить на 60.)

Решение:

34 + 46 = 80 (км/с) — скорость сближения.

15 мин = 15 · 60 = 900 (с) - до встречи.

80 · 900 = 72 000 (км)

— Как по-другому можно решить задачу?

— Что можно сделать сначала? (Перевести минуты в секунды.)

— Что можно найти потом? (Расстояния, которые пролетят комета и космический корабль за это время.)

— Что узнаем последним действием? (Все расстояние, которое будет между ними до встречи.)

Решение:

15 мин = 15 · 60 = 900 (с) — до встречи.

46 · 900 = 41 400 (км) - пролетит комета.

34 - 900 = 30 600 (км) — пролетит космический корабль.

41400 + 30 600 = 72 000 (км)

(Ответ: 72 000 км.)

X. Повторение изученного материала

1. № 288 стр. 47 (один ученик решает на обратной стороне доски, остальные — в тетрадях).

— Что значит сократить дробь?

— Какая дробь получается в результате сокращения? (Несократимая, равная данной дроби.)

Решение:

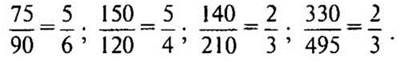
— Что интересного заметили? (При сокращении последних двух дробей получилась дробь 2/3.)

— Что можете сказать о дробях, которые надо было сокращать? (Последние две дроби равны.)

XI. Самостоятельная работа (можно выставить оценки)

Вариант I

1. № 253 стр. 40 (записать промежуточные ответы).

2. № 294 (1) стр. 47.

3. № 295 (1, 2) стр. 47.

Вариант II (для более подготовленных учеников)

1. № 284 стр. 46 (записать промежуточные ответы).

2. № 294 (2) стр. 47.

3. № 295 (3, 4) стр. 47.

XII. Подведение итогов урока

— Можно ли привести дробь 2/7 к знаменателю 35? К знаменателю 25?

— Какое число называют дополнительным множителем?

— Как найти дополнительный множитель?

Домашнее задание: № 297 (а, б), 300 (а—в), 301, 303 (а) стр. 48.