Пропорции - ОТНОШЕНИЯ И ПРОПОРЦИИ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: ввести понятие пропорции, ее членов; научить составлять пропорции из отношений: ознакомить с двумя способами проверки верной пропорции; развивать грамотную математическую речь.

Информация для учителя

Чтобы проверить, верно ли составлена пропорция, можно:

1 способ

1. Вычислить числовое значение каждого отношения, составляющего пропорцию.

2. Если отношения равны, то пропорция составлена верно.

3. Если отношения не равны, то пропорция составлена неверно.

2 способ (основан на использовании основного свойства пропорции)

1. Найти произведение крайних членов пропорции.

2. Найти произведение ее средних членов пропорции.

3. Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний учащихся

1. Познакомить учащихся с результатами самостоятельной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

III. Устный счет

1. Найдите: 10% от 500; 40% от 300; 125% от 200: 50% от 620: 250% от 800.

— Как найти процент от числа?

2. Найдите значение выражений: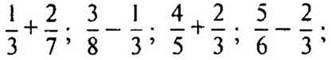

3. Сосчитайте количество треугольников на чертеже.

4. На столе горят 7 свечей, 3 свечи потушили. Сколько свечей останется на столе через 5—6 часов? (3.)

5. Сторона квадрата 6 см. На сколько увеличится периметр этого квадрата, если каждая сторона увеличится на 3 см? Что произойдет с площадью квадрата?

IV. Индивидуальная работа

Работу 1-го и 2-го уровня проверяют сильные учащиеся; работу повышенного уровня проверяет учитель.

1 карточка. I уровень

Решите уравнения относительно х:

2 карточка. II уровень

Решите уравнения относительно x:

3 карточка. Повышенный уровень Решите уравнения относительно х:

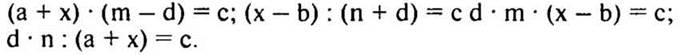
V. Сообщение темы урока

— Прочитайте слово: я и о о п п р р ц. Правильно: пропорция. Сегодня на уроке мы познакомимся с пропорциями, узнаем, что они могут быть верными и неверными, научимся составлять верные пропорции.

VI. Изучение нового материала

1. Подготовительная работа.

— Придумайте отношение, равное 5.

Записать на доске все ответы.

— Если наши отношения равны 5, я могу составить из них равенства:

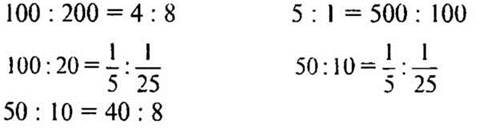
— Как по-другому записать данное равенство? (Записать частное в виде дроби.)

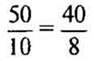
Определение. Равенство двух отношений называют пропорцией.

2. Работа над новой темой.

а) Запишем пропорцию в буквенном виде: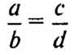

а : b = с : d

Будем считать, что а ≠ 0; b ≠ 0; с ≠ 0; d ≠ 0.

— Читают: отношение а к b равно отношению с к d.

— Или «а так относится к b, как с относится к d».

— Прочитайте по-разному пропорции, записанные на доске.

— Числа а и d называют крайними членами пропорции, а числа b и с — средними членами.

— Назовите крайние и средние члены пропорций.

б) Рассмотрим первую пропорцию: 100 : 200 = 4:8.

— Найдем произведение ее крайних и произведение ее средних членов.

— Сравните эти произведения. (Они равны.)

100 · 8 = 800

200 · 4 = 800

100 · 8 = 200 · 4

— Проверьте еще две пропорции.

— Что интересного заметили?

— Какой вывод можно сделать? (Произведение крайних членов равно произведению средних членов.)

— Я еще добавлю, что это справедливо для пропорции, которая называется верной.

— В верной пропорции произведение крайних членов равно произведению средних членов.

— Сформулируйте обратное утверждение. (Если произведение крайних членов равно произведению средних членов, то пропорция верна.)

— Это свойство называется основным свойством пропорции.

— Запишем это свойство в буквенном виде: а · d = b · с.

Запись в тетради:

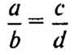
крайние члены

средние члены

a и d — крайние члены

b и с — средние члены

а ≠ 0; b ≠ 0; с ≠ 0; d ≠ 0.

а · d = b · с

VII. Физкультминутка

VIII. Закрепление изученного материала

№ 760 стр. 125.

Решение:

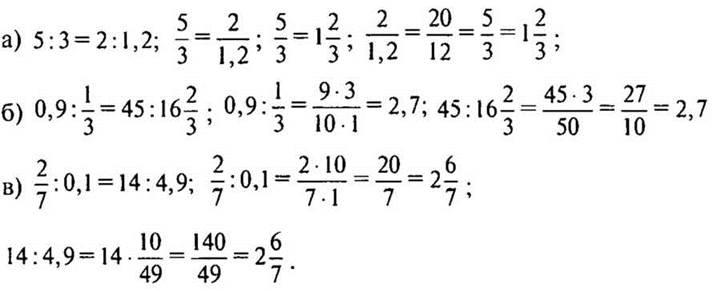
— Какой вывод можно сделать? (Так как отношения равны, то пропорции составлены верно.)

— Чтобы проверить, верно ли составлена пропорция, можно вычислить числовое значение каждого отношения.

— Если отношения равны, то пропорция составлена верно.

— Если отношения не равны, то пропорция составлена неверно.

IX. Работа над задачей

№ 735 стр. 119 (на обратной стороне доски и в тетрадях).

— Решить задачу двумя способами.

— Разобрать только с теми учащимися, которые не понимают, как решать. Они решают только одним способом.

— Зная, что вместо 240 холодильников фактически выпускали 300, что можно узнать? (Сколько холодильников выпускали сверх нормы.)

— Зная, сколько холодильников выпускали сверх норы и зная норму выпуска, что можем узнать? {На сколько процентов увеличилось производство холодильников за смену.)

Решение:

1 способ

1) 300 — 240 = 60 (х.) - выпускали сверх нормы.

2) 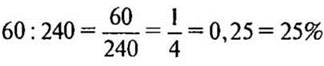- увеличилось производство холодильников за смену.

2 способ

1) 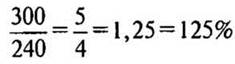— составляет выпуск холодильников сверх нормы.

2) 125 - 100 = 25%

(Ответ: 25%.)

X. Подведение итогов урока

— Что такое пропорция?

— Как называются числа х и у в пропорции х : a = b : у?

— Как называются числа а и b в пропорции х : a = b : у?

— Сформулируйте основное свойство пропорции.

Домашнее задание

№ 772, 778, 776 (а), 777 (а) стр. 127.