Координаты на прямой - урок 2 - ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА - РАЦИОНАЛЬНЫЕ ЧИСЛА

Цели: тренировать способность к обозначению рациональных чисел точками на координатной прямой и находить координаты точки по ее изображению на координатной прямой; развивать математическое мышление учащихся; формировать представления о математике как части общечеловеческой культуры.

Ход урока

I. Организационный момент

II. Устная контрольная работа

1. Верна ли пропорция: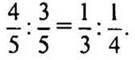

2. Решить пропорцию: 3,5 : х = 0,8 : 3,4.

3. Решить пропорцию: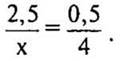

4. Составь пропорцию: 9 · 4 = 3 · 12.

5. Какую длину на плане имеет расстояние в 200 м, если масштаб 1 : 1000?

6. Какую часть числа составляет 12,5%?

7.

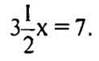
8. Найти от 7.

9.

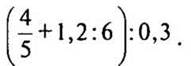
10. Что больше: 5% от 80 или 80% от 5?

III. Сообщение темы урока

— Сегодня на уроке мы продолжим изучать положительные и отрицательные числа.

IV. Изучение нового материала

— Прочитайте текст в учебнике на сгр. 150 под рубрикой «Говори правильно».

— Прочитайте правильно выражения:

а = -15; х = -0,5; у = 23; х = -6,5; а = 45;

-23 левее -4; -4 левее 3; -2 правее -9; 7 правее -3.

V. Закрепление изученного материала

1. Дайте определение координаты точки.

С помощью модели координатной прямой покажите, где расположены точки О (0), А (1), В (—3), С (5,8), Д (—12,75).

2. Практическая работа.

а) № 898 стр. 150 (самостоятельно, взаимопроверка).

Можно использовать помощь учителя или консультантов.

— Какая прямая называется координатной?

— Что называют координатой точки на прямой?

б) № 905 стр. 151 (взаимопроверка).

— Положите свой термометр горизонтально.

— Что на термометре является началом отсчета?

— Отрицательные температуры расположены на термометре слева или справа от начала отсчета?

— Покажите своему товарищу на термометре — 11°С и т. д.

в) № 895 стр. 149 (на доске и в тетрадях).

— Запишите координаты каждой точки.

(Ответы: )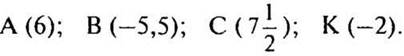

— Какой вывод можно сделать: какими числами являются координаты точек на горизонтальной прямой, расположенных: а) слева от начала координат; б) справа от начала координат?

3. № 893 стр. 149 (устно).

(Ответ: а) за 3 ч отряд пройдет 3 · 3 = 9 км, отряд может находиться или в пункте С, или в пункте D; б) за 2 ч отряд пройдет 4 · 2 = 8 км, отряд может находиться или в пункте А, или в пункте В.)

Чтобы на каждый вопрос был только один ответ, нужно добавить условие, в каком направлении двигается отряд.

4. № 918 стр. 153.

(Ответ: одна птица находится слева от узла на расстоянии 3 дм, две другие птицы находятся справа от узла на расстоянии 2 дм и 5 дм.)

VI. Физкультминутка

VII. Работа над задачей

1. № 911 стр. 152 (после разбора самостоятельно на доске и в тетрадях).

— Прочитайте задачу.

— Кто из ученых родился раньше? (Плутарх.)

— Я утверждаю, что данный ответ неверный. Почему?

— О чем мы забыли, решая эту задачу? Или на что вы не обратили внимания, когда читали задачу?

— Ведь даты жизни и смерти даны до н. э.

— Так кто же родился раньше других ученых? (Пифагор.)

— Как узнать, сколько лет прожил каждый ученый? (Из даты рождения вычесть дату смерти.)

— Запишите самостоятельно решение этой задачи.

Решение:

1) 384 - 322 = 64 (г.) - прожил Аристотель.

2) 570 - 500 = 70 (лет) — прожил Пифагор.

3) 127 - 46 = 81 (г.) - прожил Плутарх.

(Ответы: Аристотель — 64 года, Пифагор — 70 лет, Плутарх — 81 год.)

2. № 916 стр. 152—153 (после подробного разбора на обратной стороне доски и в тетрадях).

— Прочитайте задачу.

— Приведите примеры из окружающей обстановки, дающие представление о цилиндре. (Показать модели цилиндра.)

— Что называют основанием цилиндра? (Круг.)

— Сколько оснований имеет цилиндр? (2.)

— Как найти площадь круга? (S = πr2.)

— Какая геометрическая фигура является разверткой поверхности цилиндра? (Прямоугольник.)

— Как найти площадь прямоугольника? (S = ab.)

— Сколько измерений нужно знать, чтобы найти площадь прямоугольника? (Два.)

— Назовите их. (Высота — 5 см, а второе - это длина окружности основания цилиндра)

— Как найти длину окружности ? (S = 2πr.)

Решение:

1) 2 · 3,14 · 22 = 25,12 (см2) — площадь двух оснований цилиндра.

2) 2 · 3,14 · 2 = 12, 56 (см) — длина окружности основания.

3) 12,56 · 5 = 62,8 (см2) — площадь боковой поверхности цилиндра.

4) 25,12 + 62,8 = 87,92 (см2)

(Ответ: 87,92 см2.)

VIII. Повторение изученного материала

1. № 907 стр. 151 (самостоятельно, устная проверка).

2. Необходимо правильно и быстро решить примеры устно. Промежуточные ответы тоже записываем.

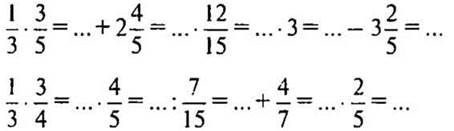
Взаимопроверка.

2. № 909 (в, г) стр. 152 (у доски и в тетрадях).

Решение: перечислить все числа, которые располагаются между данными числами, и сосчитать их.

в) 7 чисел; г) ни одного числа.

IX. Подведение итогов урока

— Какую координату имеет начало координат?

— Какими числами являются координаты точек на вертикальной прямой, расположенных: а) выше начала координат;

б) ниже начала координат?

Домашнее задание

Учебник, стр. 150 (прочитать текст под рубрикой «Говори правильно».

№ 890 (а) стр. 144; № 917 (3) стр. 153; № 921 стр. 154.