Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Касание окружностей

Окружности касаются друг друга, если они имеют единственную общую точку. Различают случаи внешнего и внутреннего касания окружностей.
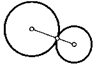
Свойство касающихся окружностей. Точка касания двух окружностей лежит на одной прямой с их центрами.
Признак касания окружностей. Если общая точка двух окружностей лежит на одной прямой с их центрами, то окружности касаются.
1. Докажите свойство касающихся окружностей.
2. Докажите, что в точке касания две окружности имеют общую касательную прямую, а расстояние между центрами окружностей равно сумме или разности их радиусов.
К задаче 2, 3, 4

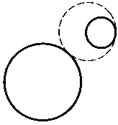
3. Две окружности касаются внешним образом, причем каждая из них касается изнутри окружности радиуса R. Найдите периметр треугольника, образованного центрами этих окружностей.
4. Радиусы двух окружностей равны 2 и 5, а расстояние между их центрами равно 10. Третья окружность касается одной из них внешним образом, а другой — внутренним образом. Докажите, что радиус третьей окружности не меньше 3,5.
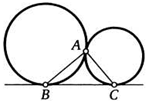
5. Две окружности касаются в точке А. Прямая касается обеих окружностей в точках В и С. Найдите угол ВАС.
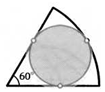
6. Дан сектор круга радиуса R с углом 60°. Найдите радиус окружности, вписанной в сектор.
7. Две касающиеся окружности вписаны в угол 60°. Найдите отношение их радиусов.
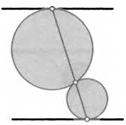
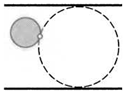
8. Две окружности касаются внешним образом, причем каждая из них касается одной из двух параллельных прямых так, как это показано на рисунке. Докажите, что три получившиеся точки касания лежат на одной прямой.
9. Три окружности касаются друг друга внешним образом. Две прямые, проходящие через точки их касания, вторично пересекают одну из этих окружностей в двух точках. Докажите, что эти две точки диаметрально противоположны.

10. В трапецию можно вписать окружность. Докажите, что окружности, построенные на ее боковых сторонах как на диаметрах, касаются друг друга.
11. Две окружности с радиусами R и г внутренним образом касаются третьей окружности в точках А и В. Оказалось, что одна из точек их пересечения лежит на отрезке АВ. Найдите радиус третьей окружности.
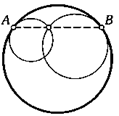
12. (Лемма Архимеда.) Хорда разбивает окружность на две дуги. Другая окружность касается данной хорды и одной из данных дуг. Докажите, что прямая, проходящая через точки ее касания, делит вторую дугу пополам.
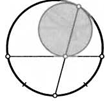
13. Сформулируйте и докажите утверждение, аналогичное лемме Архимеда, для случая внешнего касания окружностей, показанного на рисунке.
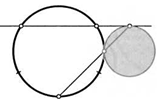
14. Постройте окружность, касающуюся двух параллельных прямых и данной окружности (разберите случаи внешнего и внутреннего касания).
15. Вокруг окружности описан четырехугольник. Диагональ разбивает его на два треугольника. Докажите, что вписанные в них окружности касаются друг друга.
16. В треугольник вписана окружность. Одну из точек касания соединили с противоположной вершиной. Полученный отрезок разбивает данный треугольник на два треугольника. Докажите, что их вписанные окружности касаются.

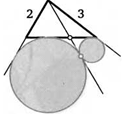
17. Две стороны треугольника равны 2 и 3. Через их общую вершину провели прямую так, что отмеченные на рисунке окружности касаются. В каком отношении данная прямая делит третью сторону треугольника, если эта сторона равна 4?
18. Три окружности касаются друг друга внешним образом. Докажите, что окружность, проходящая через три точки их касания, вписана в треугольник, образованный центрами окружностей.

19. Постройте три окружности, которые попарно касались бы друг друга внешним образом в трех заданных точках.
20. Постройте три окружности, две из которых внешним образом касались бы в точке Л, а в точках В и С касались бы изнутри третьей окружности.
*21. Две окружности внешним образом касаются в точке В, а в точках Л и С касаются третьей окружности изнутри. Оказалось, что радиус третьей окружности равен радиусу окружности, проходящей через точки А, В и С. Найдите угол АВС.
