Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Признаки вписанного четырехугольника

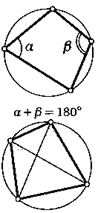
Свойство ВПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА. Сумма противоположных углов вписанного четырехугольника равна 180°.

Первый признак вписанного четырехугольника. Если сумма противоположных углов четырехугольника равна 180°, то его можно вписать в окружность.

Второй признак вписанного четырехугольника. Если одна сторона выпуклого¹ четырехугольника видна из двух его вершин под равными углами, то этот четырехугольник можно вписать в окружность.

1. Приведите пример четырехугольника, который нельзя вписать в окружность.

2. Используя приведенный чертеж, докажите первый признак вписанного четырехугольника.

С

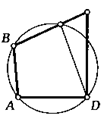
3. Используя приведенный чертеж, докажите второй признак вписанного четырехугольника.

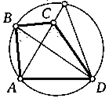
4. Дан четырехугольник ABCD, в котором /.ВАС = 30°, /ВСА — = 40°, ZCAD — 50°, ZACD = 60°. Найдите угол между его диагоналями.

5. Диагонали трапеции образуют равные углы с ее боковыми сторонами так, как показано на рисунке. Докажите, что трапеция равнобокая.

6. Вне квадрата ABCD взята такая точка М, что угол ВМС равен 135°. Найдите угол AMD.

7. Вне равностороннего треугольника АВС взяли точку Е так, что угол ВЕС прямой. Точка М —середина АС. Найдите угол МЕС. Будьте внимательны: в задаче есть разные случаи!

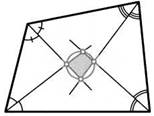
8. Докажите, что биссектрисы всех углов выпуклого четырехугольника при пересечении образуют вписанный четырехугольник.

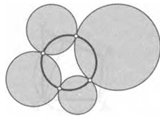
9. Четыре круга расположены так, что каждый из них касается двух других внешним образом. Докажите, что четыре точки их касания лежат на одной окружности.

10. В треугольнике АВС проведены высоты AM и СК. Докажите, что угол ВКМ равен углу АСВ.

11. В треугольнике АВС проведены высоты AM и СК. Точка О — центр его описанной окружности. Докажите, что ВО ±МК.

12. Две вершины прямоугольного треугольника «скользят» по сторонам прямого угла. Докажите, что третья его вершина движется по прямой.

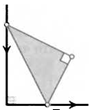
13. В треугольнике АВС провели высоту ВН. Точки D и Е — проекции точки Н на стороны АВ и ВС. Докажите, что точки A, D, Е и С лежат на одной окружности.

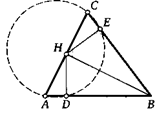
14. (Теорема о высотах треугольника.) Используя вписанные углы, докажите, что высоты любого треугольника пересекаются в одной точке.

15. Основания высот остроугольного треугольника образуют новый треугольник. Докажите, что в этом треугольнике данные высоты являются биссектрисами.

16. На диагонали трапеции ABCD с основаниями AD и ВС опущены перпендикуляры BE и СК. Докажите, что точки А, Е, К и D лежат на одной окружности.

17. В треугольнике провели три высоты. Из основания одной из них опустили перпендикуляры на две другие высоты и на две стороны треугольника. Докажите, что основания всех этих перпендикуляров лежат на одной прямой.

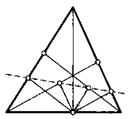
18. Через концы боковой стороны равнобокой трапеции и точку пересечения ее диагоналей провели окружность. Докажите, что она проходит через центр окружности, описанной вокруг трапеции.

19. На сторонах АВ, ВС и АС треугольника АВС выбраны соответственно точки М, К и Е так, что /АЕМ = /.СЕК = /АВС. Отрезки АК и СМ пересекаются в точке О. Докажите, что четырехугольник ОМВК вписанный.

В

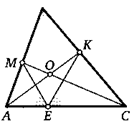
20. В четырехугольнике ABCD углы В и D прямые. Через точку О пересечения его диагоналей проведена прямая, перпендикулярная АС. Докажите, что отрезок этой прямой, заключенный внутри четырехугольника, делится точкой О пополам.

D

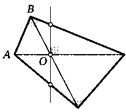
21. Из точки М к окружности проведены касательные МА, МВ и произвольная прямая, пересекающая окружность в точках Р и Q. Точка Е — середина хорды PQ. Докажите, что угол АЕМ равен углу ВЕМ.

М

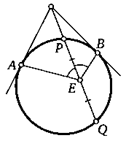
22. Из точки пересечения диагоналей вписанного в окружность четырехугольника опущены перпендикуляры на его стороны. Докажите, что основания этих перпендикуляров образуют четырехугольник, в который можно вписать окружность.

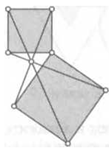
23. Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки пересекаются в одной точке.

24. На сторонах произвольного треугольника АВС вне его построили равносторонние треугольники АВК, ВСЕ и ACM. Докажите, что отрезки АЕ, ВЫ и С К равны и пересекаются в одной точке.

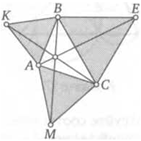
25. Через середину Р дуги MN окружности проведены две прямые, пересекающие стягивающую ее хорду в точках Л и Б, а окружность—в точках С и D. Докажите, что точки А, В, С и D лежат на одной окружности.

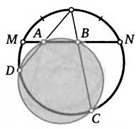
26. В треугольнике АВС проведены высоты АЕ и СК. Прямая КЕ пересекает описанную окружность в точках М и Р. Докажите, что ВМ = ВР.

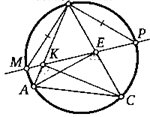
27. На каждой стороне треугольника отметили по точке. Докажите, что три отмеченные на рисунке окружности пересекаются в одной точке.

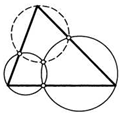
28. Нарисуйте соответствующий чертеж и докажите утверждение предыдущей задачи для случая, когда указанные в ней окружности пересекаются вне треугольника.

29. (Задача Наполеона.) На сторонах произвольного треугольника построили равносторонние треугольники. Докажите, что их центры образуют также равносторонний треугольник.

30. Четыре пересекающиеся прямые образуют четыре треугольника. Докажите, что четыре окружности, описанные вокруг них, пересекаются в одной точке (точке Микеля).

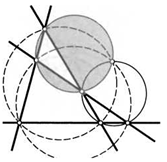
31. Пятиугольная звезда вписана в окружность. Отмеченный на рисунке пунктиром отрезок параллелен ее звену АС. Докажите, что тогда АВ = ВС.

32. Докажите, что основания перпендикуляров, опущенных из произвольной точки описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой (прямая Симпсона).

33. Дан четырехугольник ABCD, в котором /.АВС = 120°, /АСВ = 20°, ZADB = 40° и /BDC = 80°. Найдите угол между его диагоналями.

34. Биссектриса треугольника делит пополам угол между его медианой и высотой, проведенными из той же вершины. Докажите, что треугольник прямоугольный.

35. Точка Е — середина стороны AD квадрата ABCD. На отрезок BE опущен перпендикуляр АН. Найдите угол BHD.

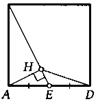
36. Биссектрисы АЕ и СК треугольника АВС пересекаются в точке О. Известно, что угол АВС равен 60°. Докажите, что ОЕ = СК.

37. Окружность, вписанная в треугольник АВС, касается сторон АВ и ВС в точках М и К. Биссектриса угла А пересекает прямую МК в точке Е. Докажите, что угол АЕС прямой.

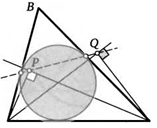
38. На биссектрисы углов А и С треугольника АВС опустили перпендикуляры АР и CQ. Докажите, что прямая PQ проходит через точки касания со сторонами вписанной в треугольник АВС окружности.

Л

С

39. Стороны АВ и CD ромба ABCD видны из некоторой точки М под углами 80° и 100°. Под какими углами видны из этой точки стороны AD и ВС?

*40. В треугольнике АВС провели медиану ВМ. Оказалось, что сумма углов АВМ и АСВ равна 90°. Докажите, что данный треугольник либо равнобедренный, либо прямоугольный.