Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Обратный ход
Смысл данного приема заключается в том, что мы угадываем, где лежит данная точка в треугольнике: на пересечении биссектрис, высот, серединных перпендикуляров к его сторонам или других геометрических мест, связанных с треугольником. А потом доказываем, что другой такой точки не существует. Конечно, в каждом конкретном случае не исключено, что задачу можно решить и другим способом.
1. В остроугольном треугольнике АВС взяли точку М так, что ZAMC 4- ZABC = 180°, ZAMB 4- ZACB = 180°. Докажите, что точка М — ортоцентр треугольника АВС.
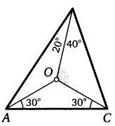
2. В треугольнике АВС взята точка О так, что ZACO = ZCAO = = 30°, ZABO = 20°, ZCBO = 40°. Найдите ZBOC.
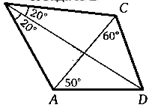
3. Дан выпуклый четырехугольник ABCD, в котором ZBDC = = 2ZBAC, ZADB = 2ZBCA. Докажите, что треугольник ADC равнобедренный.
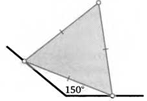
4. Две вершины равностороннего треугольника скользят по разным сторонам угла, равного 150°. По какой траектории движется его третья вершина?
5. В треугольнике АВС взята точка М так, что ZMAC = 20°, ZMCA — 30°, а углы АВМ и СВМ равны 40°. Найдите ZBMC.
6. Дан четырехугольник ABCD, в котором ZDAC — 50°, ZDCA — — 60°, а углы ABD и CBD равны 20°. Найдите угол между его диагоналями.
7. На медиане ВЫ треугольника АВС взяли точку О так, что ZAOC + ZABC = 180°. Докажите, что окружности, описанные вокруг треугольников АВО и СВО, касаются прямой АС.
8. В четырехугольнике ABCD биссектрисы углов В и С пересекаются в точке М. Оказалось, что ZBMC 4- ZAMD = 180°. Докажите, что в данный четырехугольник можно вписать окружность.
9. Четырехугольник ABCD можно вписать в окружность. Сколько существует внутри него таких точек М, что ZABM = ZDCM, ZCBM = ZDAM1
10. Точка О — центр окружности, вписанной в четырехугольник ABCD. Перпендикуляры, восстановленные в его вершинах к отрезкам АО, ВО, СО и DO, образуют новый четырехугольник. Докажите, что точка О лежит на пересечении диагоналей нового четырехугольника.
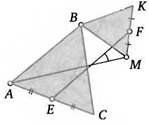
11. Равносторонние треугольники ЛВС и ВМК имеют общую вершину. Точки Е и F — середины отрезков АС и КМ соответственно. Найдите угол между прямыми AM и EF.
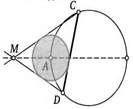
12. Отрезок ЛВ является диаметром окружности и пересекает ее хорду CD. Другая окружность имеет центр в точке А и касается хорды CD. К этой окружности из точек С и D провели касательные. Докажите, что они пересекаются на прямой ЛВ.
*13. Один катет и гипотенуза прямоугольного равнобедренного треугольника видны из некоторой точки под углами 135°. Докажите, что данная точка лежит на медиане треугольника.