Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Теорема Пифагора
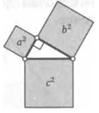
а2 + Ъ2 = с2
В современной формулировке эта знаменитая теорема звучит так: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.
Древние же греки, которые все переводили на геометрический язык, говорили так: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
1. Покажите на клетчатой бумаге два узла, не лежащие на одной линии сетки, расстояние между которыми равно 5 клеткам.
2. Верно ли, что треугольник, изображенный на клетчатой бумаге, прямоугольный?

3. На клетчатой бумаге нарисуйте квадрат так, чтобы все его вершины лежали в узлах сетки, а площадь равнялась бы 41 клетке.
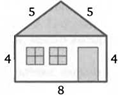
4. Определите высоту дома, ширина фасада которого равна 8 метрам, высота от фундамента до крыши равна 4 метрам, а длина ската крыши равна 5 метрам.
5. Основания равнобокой трапеции равны 1 и 2, а ее площадь равна 3. Найдите диагональ трапеции.
6. Стороны треугольника равны 5, 12 и 13. Докажите, что он прямоугольный.
7. Две стороны треугольника равны 3 и 5, а медиана, проведенная к третьей, равна 2. Найдите площадь треугольника.
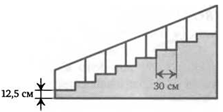
8. Лестница состоит из 40 ступеней. Высота каждой ступени равна 12,5 см, ширина —30 см. Определите длину перил лестницы.
9. Даны три отрезка с длинами а, Ъ и с. Как циркулем и линейкой построить отрезок, равный у/a2 + Ь2 + с2?
10. Стороны треугольника равны 2, 3 и 4. В каком отношении делит его высота большую из них?
11. Боковые стороны равнобедренного треугольника равны 5, а его основание равно 6. Найдите радиус описанной окружности.
12. Основания равнобокой трапеции равны 6 и 8, а ее высота равна 1. Найдите радиус описанной окружности трапеции.
13. На стороне квадрата как на диаметре построена окружность. Из его вершины, не лежащей на окружности, к ней проведена касательная. В каком отношении эта касательная делит сторону квадрата?

14. Бумажный квадрат перегнули так, что одна его вершина оказалась в середине не содержащей ее стороны. В каком отношении точка К, лежащая на линии сгиба, делит сторону квадрата?

15. На сколько километров удалена от человека, стоящего на берегу моря, линия горизонта? (Средний рост человека —1,7 м, радиус Земли — 6400 км.)
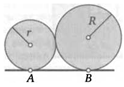
16. Две окружности радиусов R и г касаются друг друга внешним образом, а также одной прямой в точках А и В. Докажите, что расстояние между точками их касания с прямой вычисляется по формуле АВ = 2 у/Ш.
17. Диагонали прямоугольной трапеции перпендикулярны, а ее основания равны 2 и 8. Найдите высоту трапеции.
2
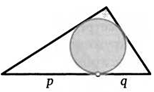
18. Окружность, вписанная в прямоугольный треугольник, делит его гипотенузу на отрезки с длинами р ид. Найдите площадь треугольника.
19. Диагонали трапеции перпендикулярны, а их длины равны 6 и 8. Найдите высоту трапеции.
Среднее геометрическое
20. Найдите высоту прямоугольного треугольника, если длины отрезков, на которые она разбивает гипотенузу, равны а и Ь.
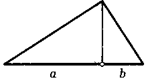
21. Геометрически докажите, что у/ab < (a4-b)/2.
22. Даны два отрезка с длинами а и Ь. Циркулем и линейкой постройте их среднее геометрическое, то есть отрезок, длина которого равна у/ab.
23. Дан единичный отрезок. С помощью циркуля и линейки постройте отрезки с длинами v2, y/l + у/2.
24. Даны отрезки с длинами а, Ъ, с и d. Как циркулем и линейкой построить отрезок, равный Vab + cd ?
25. Постройте квадрат, равновеликий а) данному прямоугольнику; б) данному четырехугольнику.
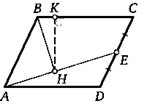
26. Точка Е — середина стороны CD параллелограмма ABCD. На отрезок АЕ опустили перпендикуляр ВН. На сторону ВС опустили перпендикуляр НК. Найдите НК, если ВХ = 2, С7С = 3.
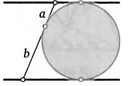
27. Окружность касается двух параллельных прямых и секущей, причем точка касания делит секущую на два отрезка с длинами а и Ь. Найдите радиус окружности.
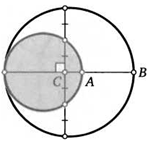
28. Две окружности касаются внутренним образом. Линия их центров вторично пересекает меньшую окружность в точке А, а большую —в точке Б. Хорда большей окружности, перпендикулярная прямой АВ, пересекает ее в такой точке С, что эта точка и меньшая окружность делят хорду на четыре равные части. Найдите АС: АВ.
Четырехугольник с перпендикулярными диагоналями
29. (Теорема о четырехугольнике с перпендикулярными диагоналями.) а) Диагонали выпуклого четырехугольника перпендикулярны. Докажите, что суммы квадратов его противоположных сторон равны, б) Докажите обратное утверждение.
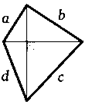
a2 + c2 = b2 + d2
30. Две медианы треугольника перпендикулярны друг другу. Докажите, что его стороны удовлетворяют соотношению а2 4- Ъ2 = 5с2.
31. В шестиугольнике ABCDEF углы А и С прямые, причем АВ = ВС, CD = DE, EF = FA. Докажите, что прямые BE и FD перпендикулярны.
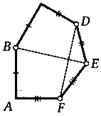
32. Внутри прямоугольника взяли точку. Оказалось, что расстояния от нее до трех его вершин равны последовательно 1, 7 и 8. Найдите расстояние от данной точки до четвертой вершины.
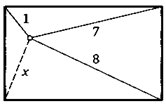
33. Радиусы двух окружностей равны 5 и 20, а расстояние между их центрами —16. Найдите сторону ромба, две противоположные вершины которого лежат на одной окружности, а две оставшиеся — на другой.
Разные задачи
34. Окружность радиуса 1 разбили на 10 равных частей. Найдите сумму квадратов расстояний от произвольной точки окружности до всех 10 точек деления.
35. Один конец меньшего основания трапеции равноудален от концов ее большего основания, а из другого конца меньшего основания большее основание видно под прямым углом. Найдите площадь трапеции, если ее основания равны 2 и 5.
2

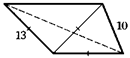
36. Одна вершина трапеции удалена от трех других ее вершин на расстояние 13. Найдите диагональ трапеции, не выходящую из этой вершины, если другая ее боковая сторона равна 10.
37. (Доказательство Евклида теоремы Пифагора.) Перпендикуляр, опущенный из вершины прямого угла на гипотенузу треугольника, делит построенный на ней квадрат на два прямоугольника. Докажите, что площади этих прямоугольников равны площадям квадратов, построенных на катетах треугольника. Выведите отсюда теорему Пифагора.
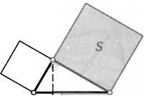
S
38. Выразите радиус вписанной в прямоугольный треугольник окружности через его стороны, а его площадь через этот радиус и докажите теорему Пифагора.
39. Восстановите по чертежу Леонардо да Винчи данное им доказательство теоремы Пифагора.

40. Катеты прямоугольного треугольника равны а и Ь, его гипотенуза равна с, а высота, опущенная на гипотенузу, равна h. Докажите, что из отрезков a + b, h и c + h можно построить прямоугольный треугольник. Чему равна его гипотенуза?
41. Из точки М к окружности проведены две касательные. На прямой, проходящей через середины получившихся отрезков, выбирается любая точка О. Докажите, что длина касательной OL, проведенной из нее к окружности, равна ОМ.
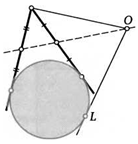
Конфигурационные задачи
42. Цветок лилии возвышается над поверхностью озера на 10 см, а если его потянуть за стебель, он коснется воды в метре от своего прежнего положения. Определите глубину озера в данном месте.
43. На стороне квадрата взяли точку так, что она равноудалена от одной его вершины и середины соседней стороны (см. рисунок). В каком отношении эта точка делит сторону квадрата?
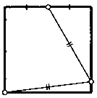
44. Сторона квадрата равна 1. Найдите сторону равностороннего треугольника, одна вершина которого совпадает с вершиной квадрата, а две другие лежат на его сторонах.
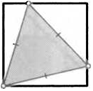
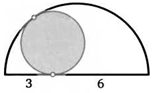
45. Точка касания окружности, вписанной в полукруг, делит его диаметр на два отрезка с длинами 3 и 6. Найдите радиус этой окружности.
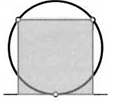
46. Найдите сторону квадрата, две вершины которого лежат на окружности радиуса 1, а две другие — на касательной к ней.
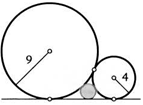
47. Две окружности радиусов 4 и 9 касаются внешним образом. Найдите радиус третьей окружности, касающейся данных, а также их общей внешней касательной. Сколько решений имеет задача?
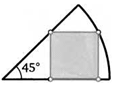
48. В сектор круга радиуса 1 с углом 45° вписан квадрат, так что одна его вершина лежит на окружности. Найдите площадь квадрата.
49. Квадрат со стороной 1 вписан в окружность. Найдите сторону квадрата, вписанного в один из получившихся сегментов.
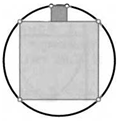
50. В сектор круга радиуса 1 с углом 90° вписали квадрат так, что две его вершины лежат на окружности. Найдите площадь квадрата.
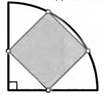
51. Сторона большого квадрата, вписанного в полукруг, равна 1. Найдите сторону маленького квадрата на рисунке.
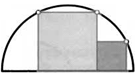
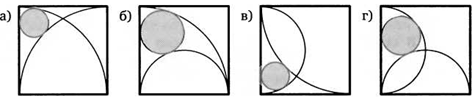
52. Сторона квадрата равна 1. На рисунках проведены окружности, центры которых лежат либо в вершинах квадрата, либо в серединах его сторон. Найдите радиусы закрашенных окружностей на рисунках.
53. Катеты прямоугольного треугольника равны а и Ь, а его гипотенуза — с. Найдите радиус окружности, которая касается катетов, а также изнутри касается описанной окружности треугольника.
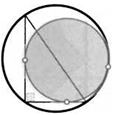
54. Сторона квадрата равна 1. Найдите сторону закрашенного квадрата на рисунке.
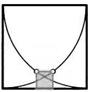
55. (Задача Архимеда.) Хорда делит круг на два сегмента. В каждый из них вписано по окружности, касающейся ее в середине. Кроме того, в каждый сегмент вписали еще по одной окружности, которые касаются первых двух. Докажите, что их радиусы равны. Найдите их радиус, если радиусы первых двух окружностей равны Яи г.
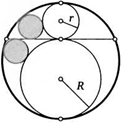
*56. В окружность с радиусом 1 вписан равносторонний треугольник. Найдите сторону квадрата, две вершины которого лежат на окружности, а две оставшиеся — на двух сторонах треугольника. Обратите внимание на то, что существуют как симметричный, так и несимметричный случаи расположения квадрата!