Гравитационная сила. Закон всемирного тяготения - ВВЕДЕНИЕ. ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Цель: изучить закон всемирного тяготения, показать его практическую значимость.

Ход урока

I. Повторение. Беседа

1. Какое фундаментальное взаимодействие определяет силу трения?

2. Сформулируйте определение силы трения, перечислите возможные виды трения.

3. Чему равна сила трения покоя?

4. Как находится сила трения покоя?

5. Куда направлена сила трения скольжения и чему она равна?

II. Самостоятельная работа

Вариант 1

1. Как изменится сила трения скольжения при движении бруска по горизонтальной плоскости, если силу нормального давления увеличить в 2 раза?

A. Не изменится.

Б. Увеличится в 2 раза.

B. Уменьшится в 2 раза.

Г. Увеличится в 4 раза.

2. Брусок массой 0,2 кг равномерно тянут с помощью динамометра по горизонтальной поверхности стола. Показания динамометра 0,5 Н. Чему равен коэффициент трения скольжения? Ускорение свободного падения примите равным 10 м/с².

A. 0,2.

Б. 0,25.

B. 0,4.

Г. 0,5.

3. На рисунке представлен график зависимости модуля силы трения F от модуля силы нормального давления N. Определите коэффициент трения скольжения (рис. 64).

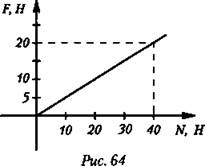
А. 0,1.

Б. 0,2.

В. 0,25.

Г. 0,5

4. Конькобежец массой 60 кг скользит по льду. Определите силу трения скольжения, действующую на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,015.

A. 400 Н.

Б. 40 Н.

B. 9 Н.

Г. 0,9 Н

5. Брусок массой m движется вверх по наклонной плоскости, коэффициент трения скольжения μ. Чему равен модуль силы трения?

A. μg.

Б. μmg.

B. μg sin α.

Г. μmg cos α.

6. Брусок массой m кг лежит на наклонной плоскости, угол наклона которой к горизонту равен α. Коэффициент трения скольжения μ. Чему равен модуль силы трения?

A. μg sin α.

Б. μmg.

B. μmg cos α.

Г. μg

Вариант 2

1. На рисунке представлены графики зависимости модуля силы трения F от модуля силы нормального давления N. В каком случае коэффициент трения больше и во сколько раз?

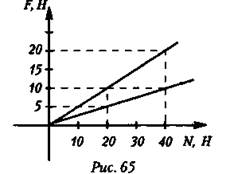
A. В первом случае; μ₁ = 4μ₂;

Б. В первом случае; μ₁ = 2μ₂;

B. Во втором случае; μ₂ = 2μ₁;

Г. Во втором случае; μ₂ = 4μ₁.

2. Брусок массой 0,2 кг прижат к вертикальной стене с силой 5 Н. Коэффициент трения между бруском и стеной равен 0,2. Чему равна сила трения скольжения бруска о стену?

A. 0,4 Н.

Б. 0,6 Н.

B. 1 Н.

Г. 1,4 Н.

3. По условиям предыдущей задачи определите минимальную силу нормального давления на брусок, чтобы он был неподвижен. Ускорение свободного падения примите равным 10 м/с².

A. 0,5 Н.

Б. 1 Н.

B. 5 Н.

Г. 10 Н.

4. Определите тормозной путь автомобиля, начавшего торможение на горизонтальном участке шоссе с коэффициентом трения 0,5 при начальной скорости движения 15 м/с. Ускорение свободного падения примите равным 10 м/с².

A. 90 м.

Б. 45 м.

B. 22,5 м.

Г. 11,25 м.

5. Автомобиль совершает поворот по дуге окружности. Каково минимальное значение радиуса окружности траектории автомобиля при коэффициенте трения автомобильных шин о дорогу 0,4 и скорости автомобиля 10 м/с? Ускорение свободного падения примите равным 10 м/с².

А. 250 м.

Б. 100 м.

В. 50 м.

Г. 25 м.

6. Брусок массой m движется вверх по горизонтальной поверхности под действием силы F, направленной под углом α. Коэффициент трения скольжения μ. Чему равен модуль силы трения?

A. μ.

Б. μmg

B. mg sin .

Г. μmg cos α

6. Брусок массой m кг лежит на наклонной плоскости, угол наклона которой к горизонту равен α. Коэффициент трения скольжения μ. Чему равен модуль силы трения?

A. F cos α.

В. F sin α.

Б. F sin α.

Г. μ(mg + A sin α)

	Номер вопроса и ответ
	1	2	3	4	5	6
Вариант 1	Б	Б	Г	В	Г	А
Вариант 2	Б	В	Г	В	Г	В

III. Изучение нового материала

Попытки объяснить строение Солнечной системы, занимали умы многих великих людей.

Особенно волновал вопрос о том, что связывает планеты и Солнце в единую систему? Он встал после того, как Коперник «поместил» Солнце в центр, а все планеты «заставил» обращаться вокруг него.

Ньютон связал силу с ускорением. Именно Солнце естественно считать причиной обращения вокруг него Земли и планет. Но не только планеты притягиваются к Солнцу. Солнце также притягивается планетами. И планеты взаимодействуют между собой.

Все тела Вселенной, как небесные, так и находящиеся на Земле, подвержены взаимному притяжению. Если мы не наблюдаем притяжения между окружающими предметам, так это только потому, что оно слишком слабо.

Взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу, называется гравитационным.

Гравитационное взаимодействие осуществляется посредством особого вида материи, называемого гравитационным полем. Такое поле существует вокруг любого тела. Особенностью гравитационного поля является его всепроникающая способность. Взаимосвязь тел с гравитационным полем характеризуют особой физической величиной - гравитационным зарядом. Гравитационный заряд любого тела равен его массе.

Одной из важнейших задач в теории тяготения является задача двух тел. Задача исследования движения и взаимодействия внутри системы, состоящей из двух тел, каждое из которых можно принять за материальную точку.

Выражение для силы тяготения Ньютон получил в 1666 г., когда ему было всего лишь 24 года.

Ньютон установил, как зависит от расстояния ускорение свободного падения. Вблизи поверхности Земли, т. е. на расстоянии 6400 км от ее центра оно составляет 9,8 м/с², а на расстоянии в 60 раз большем, у Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. 3600 = 60². Ускорение убывает обратно пропорционально квадрату расстояния от центра Земли,

Но ускорение, по второму закону Ньютона, пропорционально силе, а сила прямо пропорциональна массам:

Если ввести коэффициент пропорциональности, то (V - гравитационная постоянная)

Закон всемирного тяготения верен:

1. для материальных точек.

2. для расчета силы притяжения шарообразных тел со сферическим распределением вещества.

3. для шара большого радиуса и материальной точки.

Когда Ньютон открыл закон всемирного тяготения, он не знал ни одного числового значения масс небесных тел, в том числе и Земли, неизвестно ему было и значение постоянной G.

V можно найти, зная силу притяжения F между телами известной массы и расстоянием между ними.

Точное измерение V было впервые проделано в 1798 г. замечательным ученым Генри Кавендишем. С помощью крутильных весов Кавендиш по углу закручивания нити сумел измерить малую силу притяжения между маленькими и большими металлическими шарами. Опыты показали V ≈ 6,67 · 10^-11 [(Н·м²/кг²].

Ее физический смысл - сила, с которой притягиваются два тела массами по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга.

Опыты Кавендиша доказали, что не только планеты, но и обычные, окружающие нас в повседневной жизни тела притягиваются по тому же закону тяготения.

IV. Повторение. Беседа

1. Как формулируется закон всемирного тяготения?

2. Что называется гравитационной постоянной?

3. Каков его физический смысл?

4. Каково его значение в системе СИ?

5. Что называют гравитационным полем?

6. Зависит ли сила тяготения от свойств среды, в которой находятся тела?

V. Решение задач

1. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения. (Ответ: 1 мкН.)

2. Оценить порядок значения силы взаимного тяготения двух кораблей, удаленных друг от друга на 100 м, если масса каждого из них 10 000 т. (Ответ: порядка 1 Н.)

3. Среднее расстояние между центрами Земли и Луны равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли. В какой точке отрезка, соединяющего центр Земли и Луны, тело будет притягиваться ими с одинаковой силой? (Ответ: В точках, отстоящих на 6 земных радиусов от центра Луны).

Домашняя работа

П. 32, 33.