Графическое описание электромагнитных колебаний. Решение задач - ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ - КОЛЕБАНИЯ И ВОЛНЫ

Методические рекомендации

Третий (и желательно четвёртый) урок отводится на отработку знаний. Особое внимание уделяют конкретным приёмам. Основной метод — решение задач.

1. Графики изменения физических величин с течением времени во многих случаях удобны для описания любых процессов. На рисунке 4.7 учебника приведены графики изменения заряда на конденсаторе и силы тока в колебательном контуре. В начальный момент времени заряд на конденсаторе максимальный, сила тока в цепи равна нулю. Если колебательный контур идеальный, то электромагнитные колебания продолжаются бесконечно долго и соответственно графики бесконечно продлеваются вправо по оси.

График изменения заряда соответствует уравнению

Выражение называют фазой колебаний, а угол - начальной фазой. В начальный момент времени фаза колебаний как раз равна начальной фазе. Значение фазы колебаний определяет значение физической величины (например, заряда, силы тока и т. п.) в заданный момент времени, так как амплитудное значение величины постоянно. Вывод: фаза колебаний однозначно описывает состояние колебательной системы.

Графики, изображённые на рисунке (рисунок 4.7 учебника заносят в тетради), различаются при равной амплитуде (чего всегда можно достичь за счёт выбора единиц величин) только фазой колебаний. Сдвиг фаз составляет , причём сила тока отстаёт по фазе от заряда. Для определения разности фаз колебаний нужно формулы колебаний выразить через одну тригонометрическую функцию.

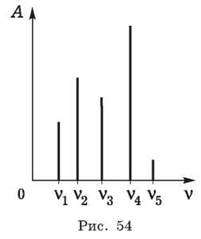
2. Иногда важно на графиках сравнить колебания лишь по частоте и амплитуде, в этом случае графики представляют собой прямые линии (рис. 54). А сами графики называют спектральным изображением. На рисунке изображены пять колебаний разной частоты и амплитуды. Максимальная частота v₅, а максимальная амплитуда колебаний у частоты v₄. Такой способ изображения важен тогда, когда сложное колебание представляют (разлагают) в виде суммы нескольких гармонических колебаний. Такое разложение и называют спектром.

3. Пример решения типичной задачи.

Колебательный контур состоит из конденсатора ёмкостью С = 400 пФ и катушки индуктивностью L = 10 мГн. Определите амплитуду колебаний силы тока, если амплитуда колебаний напряжения на конденсаторе равна 500 В.

Выделение явления. По условию задачи выделяем явление — свободные гармонические электромагнитные колебания в колебательном контуре. Вид уравнения колебаний, например силы тока, следующий: i = Icosω₀t. Как определить силу тока I?

Описание явления. Вспоминаем, что колебательный контур — это замкнутая физическая система. Для неё выполняется закон сохранения энергии. Это — важное и хорошее средство описания нашего явления. Запишем его:

Анализ уравнения убеждает в том, что, во-первых, искомая величина входит в уравнение; во-вторых, все остальные величины известны. Выразим нужную величину:

Остаётся выполнить расчёт. В результате решения получаем I = 0,1 А. Вопросы для обсуждения: точное или приближённое значение силы тока мы получили? Как это доказать? (Подсказка. Подумайте: данные ёмкости, индуктивности и напряжения — точные или приближённые значения?) Зависит ли амплитудное значение силы тока от значений ёмкости и индуктивности?

4. Задачи для самостоятельного решения: П., № 646, 648.

Вопросы для обсуждения: из чего состоит изучаемая физическая система? Какое физическое явление мы описываем?

5. Домашнее задание: § 17, 18*, 19; П., № 649, 650.