Равномерное движение точки по окружности - Кинематика - МЕХАНИКА

1.1. Кинематика

1.1.14. Равномерное движение точки по окружности

Наряду с равномерным прямолинейным движением очень часто приходится встречаться с равномерным движением по окружности. Такое движение могут совершать точки вращающихся колес, валов и роторов турбин, искусственные спутники, обращающиеся по круговым орбитам, и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.

В каждой точке круговой траектории скорость точки направлена по касательной к траектории в этой точке. В этом нетрудно убедиться, коснувшись вращающегося точильного камня, имеющего форму диска, стальным резцом: раскаленные частицы камня, имеющие в момент отрыва от него определенную скорость, будут отлетать от диска по касательной к нему. Эта скорость называется линейной скоростью вращения.

Период и частота обращения

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Известно, что при равномерном движении время определяется делением пройденного пути, т. е. длины окружности — lокр, на скорость движения. Таким образом,

Величина, обратная периоду, называется частотой обращения и обозначается буквой v.

Центростремительное ускорение

Из-за непрерывного изменения направления скорости тело, движущееся по окружности, обладает ускорением. Это ускорение характеризует не быстроту изменения численного значения скорости (которое в данном случае не меняется), а быстроту изменения ее направления.

При равномерном движении по окружности ускорение тела все время направлено к ее центру и называется центростремительным ускорением. Чтобы найти его значение, рассмотрим отношение изменения вектора скорости к малому интервалу времени , за который это изменение произошло (рис. 1.16).

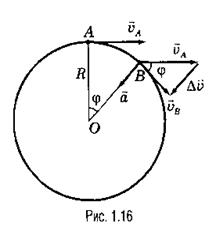
В силу малости угла φ имеем:

Так как угол φ между векторами скорости в точках А и В равен углу АОВ между радиусами, который, в свою очередь, равен отношению длины дуги АВ к радиусу R, получим:

Из формул (1.8), (1.9) и (1.12) следует, что