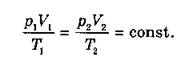Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа) - Молекулярная физика - МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА

2.1.9.Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)

Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением р, объемом V и абсолютной температурой Т, определяющими его состояние:

где В зависит от массы газа т и его молекулярной массы М. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.

В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: pV = RT, где R — универсальная газовая постоянная. Если молярная масса газа — М, то:

Уравнение состояния в форме (2.14) называется уравнением Клапейрона—Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля-Мариотта, Авогадро, Шарля.

Уравнение состояния (2.14) может быть получено из зависимости давления от температуры р = nkT (2.12), если в нее подставить концентрацию молекул n из выражения

где NA — постоянная Авогадро, N — число молекул в теле.

В результате получим:

где kNA = R — универсальная газовая постоянная, равная 8,31 · 1023 Дж/моль-К; k — постоянная Больцмана, равная 1,38 · 10-23 Дж/К. Заменив в (2.16) kNA на R, получаем уравнение состояния в виде (2.14). Отношение уравнений (2.14) или (2.13) при двух наборах параметров p1, V2, Т1 и р2, V2, Т2 дает: