Алгоритмы - Разработка и применение - 2016 год
Основные определения и применения - Графы
В этой книге мы будем в основном заниматься дискретными задачами. Если непрерывная математика занимается такими базовыми структурами, как вещественные числа, векторы и матрицы, в области дискретной математики были разработаны базовые комбинаторные структуры, заложенные в ее основу. Одной из самых фундаментальных и выразительных из таких структур является граф.
Чем больше работаешь с графами, тем скорее начинаешь замечать их повсюду. Мы начнем с базовых определений, относящихся к графам, и знакомства с целым спектром различных алгоритмических областей, в которых представление в виде графа появляется естественным образом. Затем будут рассмотрены некоторые базовые алгоритмические примитивы графов, начиная с задачи связности и разработки фундаментальных методов поиска по графу.
3.1. Основные определения и применения
Как говорилось в главе 1, граф G представляет собой обычный способ кодирования парных отношений в множестве объектов: он состоит из набора узлов V и набора ребер E, каждое из которых “соединяет” два узла. Таким образом, ребро е ∈ E представляется двухэлементным подмножеством V: e ={u, v} для некоторых u, v ∈ V, при этом u и v называются концами ребра е.
Ребра в графе обозначают симметричные отношения между их концами. Часто требуется представить асимметричные отношения; в таких случаях используется понятие направленного графа. Направленный граф G' состоит из набора узлов V и набора направленных ребер E', также называемых дугами. Каждое ребро е' ∈ E представляется упорядоченной парой (u, v); иначе говоря, роли u и v не взаимозаменяемы, узел u называется начальным, а узел v — конечным. Также говорят, что ребро е' выходит из узла u и входит в узел v.
Если требуется подчеркнуть, что рассматриваемый граф не является направленным, его называют ненаправленным графом; тем не менее по умолчанию под термином “граф” понимается именно ненаправленный граф. Также стоит сделать пару замечаний по поводу нашего использования терминологии. Во-первых, хотя ребро е в ненаправленном графе должно обозначаться как множество узлов {u, v}, чаще (и даже в книгах) используется запись, принятая для упорядоченных пар: e = (u, v). Во-вторых, узлы графа часто называются вершинами; в данном контексте эти два термина имеют абсолютно одинаковый смысл.
Примеры графов
Определить граф проще простого: возьмите набор объектов и соедините их ребрами. Но на таком уровне абстракции трудно представить типичные ситуации, в которых встречается работа с графами. По этой причине мы предлагаем список распространенных контекстов, в которых графы играют важную роль как модель. Список получился достаточно обширным, не пытайтесь запомнить все его пункты; скорее это перечень полезных примеров для проверки базовых определений и алгоритмических задач, которые встретятся нам позднее в этой главе. Кроме того, при знакомстве с примерами будет полезно поразмыслить над смыслом узлов и ребер в контексте приложения. В одних случаях и узлы и ребра соответствуют физическим объектам реального мира, в других узлы являются реальными объектами, а ребра виртуальны; наконец, и ребра и узлы могут представлять чисто абстрактные понятия.
1. Транспортные сети. Карта маршрутов компании-авиаперевозчика естественным образом образует граф: узлы соответствуют аэропортам, а ребро из узла u в v существует при наличии беспосадочного перелета с вылетом из u и посадкой в v. При таком описании граф является направленным; тем не менее на практике при существовании ребра (u, v) почти всегда существует ребро (v, u), поэтому мы практически ничего не потеряем, если будем рассматривать карту маршрутов как ненаправленный граф с ребрами, которые соединяют пары аэропортов, связанные беспосадочными перелетами. При рассмотрении такого графа (который обычно изображается на задней обложке журналов для пассажиров) можно быстро заметить несколько подробностей: часто в графе присутствует небольшое количество “центров” с очень большим количеством инцидентных ребер; и от одного узла графа можно перейти к любому другому узлу за очень небольшое количество промежуточных пересадок.
Другие транспортные сети тоже могут моделироваться подобным образом. Например, в железнодорожной сети каждый узел может представлять станцию, а ребро, соединяющее узлы u и v, — железнодорожный путь, соединяющий эти станции без промежуточных остановок. Стандартная схема метро в крупном городе представляет собой изображение такого графа.
2. Коммуникационные сети. Граф может рассматриваться как естественная модель компьютеров, объединенных в сеть передачи данных. Существуют разные способы такого моделирования. Во-первых, каждый узел может представлять компьютер, а ребро, соединяющее узлы u и v, — прямой физический канал, связывающий эти компьютеры. Кроме того, для описания крупномасштабных структур в Интернете узел часто определяется как группа машин, обслуживаемых одним интернет-провайдером; узлы u и v соединяются ребром, если между ними существует прямая одноранговая связь — проще говоря, соглашение о передаче данных по стандартному протоколу BGP, управляющему глобальной маршрутизацией в Интернете. Следует заметить, что вторая модель “виртуальнее” первой, потому что связи представляют собой формальное соглашение наряду с физической линией связи.
При анализе беспроводных сетей обычно определяется граф, узлы которого представляют собой устройства, расположенные в разных местах физического пространства, а ребро из u в vсуществует в том случае, если узел v находится достаточно близко к u для приема сигнала. Такие графы часто удобно рассматривать как направленные, потому что может оказаться, что vможет воспринимать сигнал u, а u не может воспринимать сигнал v (например, потому что на u установлен более мощный передатчик). Эти графы также интересны с геометрической точки зрения, потому что они приблизительно соответствуют размещению точек на плоскости с последующим соединением близко расположенных пар.
3. Информационные сети. Всемирная паутина может естественным образом рассматриваться как направленный граф, в котором узлы соответствуют вебстраницам, а ребро из u в v существует в том случае, если в u присутствует гиперссылка на v. Направленность графа здесь принципиальна; например, многие страницы содержат ссылки на популярные сайты новостей, тогда как на этих сайтах, естественно, обратных ссылок нет. Структура, сформированная всеми гиперссылками, может использоваться алгоритмами для определения самых важных страниц — эта методика применяется многими современными поисковыми системами.
Гипертекстовой структуре Всемирной паутины предшествовали информационные сети, появившиеся за много десятков лет до Интернета, такие как сети перекрестных ссылок между статьями в энциклопедиях или других справочниках или сети библиографических ссылок в научных статьях.
4. Социальные сети. Для любой группы людей, общающихся друг с другом (работники одной компании, студенты, жители небольшого городка), можно определить сеть, узлы которой представляют людей, а ребро между u и v существует в том случае, если они являются друзьями. Ребра также могут представлять другие отношения, помимо дружеских: ненаправленное ребро (u, v) может обозначать романтические или финансовые отношения; направленное ребро (u, v) может указывать на то, что u обращается к v за советом или u включает v в свою адресную книгу электронной почты. Также легко представить двудольную социальную сеть, основанную на концепции принадлежности: для множества X людей и множества Y организаций ребро между u ∈ X и v ∈ Y определяется в том случае, если и принадлежит организации v.
Такие сети широко применяются социологами для изучения динамики взаимодействий между людьми. В частности, они позволяют выявить наиболее “влиятельных” личностей в компании или организации, смоделировать отношения доверия в финансовой или политической среде или отследить процесс распространения слухов, анекдотов, болезней или вирусов, распространяемых по электронной почте.
5. Сети зависимостей. Модель направленного графа естественно подходит для отражения взаимозависимостей в группах объектов. Например, для учебного плана в колледже или университете каждый узел может представлять учебный курс, а ребро из u в v существует в том случае, если и является предпосылкой для v. Для списка функций или модулей крупной программной системы узел может представлять функцию, а ребро из u в v существует в том случае, если u вызывает v. Или для множества видов в экосистеме можно определить граф (пищевую сеть), в которой узлы представляют разные виды, а ребро из u в v означает, что вид u питается представителями вида v.
Этот список далеко не полон — даже для простой классификации его задач. Он просто дает примеры, о которых полезно помнить, когда мы займемся рассмотрением графов в алгоритмическом контексте.
Пути и связность
Одной из основополагающих операций с графами является обход последовательности узлов, соединенных ребрами. В приведенных выше примерах такой обход может соответствовать сеансу просмотра веб-страниц с переходами по гиперссылкам; слухам, передаваемым между людьми на другой конец света; перелету авиапассажира из Сан-Франциско в Рим с несколькими пересадками.
С учетом сказанного путь в ненаправленном графе G = (V, E) определяется как последовательность P узлов v1, v2, ..., vk-1, vk, обладающая тем свойством, что каждая очередная пара vi, vi+1соединяется ребром из G. P часто называется путем из v1 в vk, или путем v1 - vk. Например, узлы 4, 2, 1, 7, 8 образуют путь на рис. 3.1. Путь называется простым, если все его узлы отличны друг от друга. Цикл представляет собой путь v1, v2, ..., vk-1, vk, в котором k > 2, первые k - 1 узлов различны, а v1 = vk, — другими словами, последовательность узлов, которая “возвращается” к своему началу. Все эти определения естественным образом переносятся на направленные графы со следующим изменением: в направленном пути или цикле каждая пара последовательных узлов обладает тем свойством, что (vi, vi+1) является ребром. Другими словами, последовательность узлов в пути или цикле должна учитывать направленность ребер.
Ненаправленный граф называется связным, если для каждой пары узлов u и v существует путь из u в v. Для направленных графов способ определения связности не столь очевиден: может оказаться, что в графе существует путь из u в v, тогда как пути из v в u не существует. Направленный граф называется сильно связным, если для каждых двух узлов u и v существует путь из uв v, и путь из v в u.
Кроме самого факта существования пути между парой узлов u и v нам, возможно, понадобится узнать, существует ли короткий путь. Расстояние между двумя узлами нами u и v определяется как минимальное количество ребер в пути u-v. (Для обозначения расстояния между узлами, между которыми не существует соединяющего пути, можно использовать условный знак — например, да). Чтобы понять, откуда происходит термин “расстояние”, вообразите G как представление коммуникационной или транспортной сети; для перехода из u в v хотелось бы выбрать маршрут с минимальным количеством “пересадок”.
Деревья
Ненаправленный граф называется деревом, если он является связным и не содержит циклов. Например, два графа на рис. 3.1 являются деревьями. Строго говоря, деревья составляют простейшую разновидность связных графов: удаление любого узла из дерева приведет к нарушению его связности.
Для рассмотрения структуры дерева T удобно представить некоторый узел r как корень дерева. По сути, дерево “цепляется” за узел r, а остальные его ветви свисают вниз под действием силы тяжести. А если выражаться точнее, каждое ребро T “ориентируется” в направлении от г; для каждого из остальных узлов v родительским называется узел u, который непосредственно предшествует v на пути из r; узел w называется дочерним по отношению к v, если v является родительским узлом для w. В более общей формулировке узел w называется потомкомv (а v — предкомw), если v лежит на пути от корня к w; узел х называется листовым (или просто листом), если у него нет потомков. Таким образом, две диаграммы на рис. 3.1 изображают одно и то же дерево T — те же пары узлов, соединенные ребрами, но правая диаграмма представляет дерево, полученное в результате назначения узла 1 корнем T.
Корневые деревья относятся к числу фундаментальных объектов в теории программирования, потому что они представляют концепцию иерархии. Например, корневое дерево на рис. 3.1 может служить представлением организационной структуры небольшой компании с 9 работниками: работники 3 и 4 подчиняются работнику 2; работники 2, 5 и 7 подчиняются работнику 1 и т. д. Многие сайты имеют иерархическую структуру для упрощения навигации. Например, на типичном сайте кафедры информатики главная страница является корневой; страница Люди (и Учебные курсы) является дочерней по отношению к корневой; страницы Преподаватели и Студенты являются дочерними по отношению к странице Люди; домашние страницы профессоров являются дочерними по отношению к странице Преподаватели и т. д.
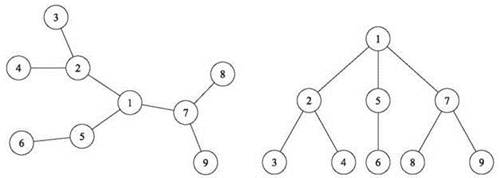
Рис. 3.1. Два представления одного дерева. В правой части хорошо видно, что узел 1 является корнем дерева
Для наших целей определение корня дерева T может концептуально упростить ответы на некоторые вопросы по поводу T. Например, если имеется дерево T с n узлами, сколько ребер оно имеет? У каждого узла, отличного от корня, имеется одно ребро, ведущее “наверх” по направлению к родителю; и наоборот, каждое ребро ведет вверх ровно от одного некорневого узла. Это позволяет очень легко доказать следующий факт.
(3.1) Каждое дерево из n узлов содержит ровно n - 1 ребро.
Более того, истинно и следующее — более сильное — утверждение, хотя здесь его доказательство не приводится.
(3.2) Допустим, G — ненаправленный граф с n узлами. Если истинны любые два из следующих утверждений, то автоматически выполняется и третье.
(i) Граф G является связным.
(ii) Граф G не содержит циклов.
(iii) Граф G содержит n - 1 ребро.
А теперь обратимся к роли деревьев в фундаментальной алгоритмической идее обхода графа.