Связность графа и обход графа - Графы

Итак, мы сформулировали некоторые фундаментальные понятия, относящиеся к графам. Пора перейти к одному из важнейших алгоритмических вопросов: связности узлов. Допустим, имеется граф G = (V, E) и два конкретных узла s и t. Нужно найти эффективный алгоритм для получения ответа на следующий вопрос: существует ли в G путь из s в t? Будем называть его задачей проверки связности s-t.

Для очень малых графов бывает достаточно взглянуть на граф. Но для больших графов поиск пути может потребовать определенной работы. Более того, задача связности s-t также может рассматриваться как задача поиска пути в лабиринте. Если представить G как лабиринт, комнаты которого соответствуют узлам, а коридоры — ребрам, соединяющим узлы (комнаты), то задача заключается в том, чтобы начать с комнаты s и добраться до другой заданной комнаты t. Несколько эффективный алгоритм можно разработать для этой задачи?

Рис. 3.2. На этом графе существуют пути от узла 1 к узлам 2-8, но не к узлам 9-13

В этом разделе описаны два естественных алгоритма для решения этой задачи на высоком уровне: поиск в ширину (BFS, Breadth-First Search) и поиск в глубину(DFS, Depth-First Search). В следующем разделе мы обсудим эффективную реализацию обоих алгоритмов на основании структуры данных для представления графа, описывающего входные данные алгоритма.

Поиск в ширину

Вероятно, простейшим алгоритмом для проверки связности s-t является алгоритм поиска в ширину(BFS), при котором просмотр ведется от s во все возможных направлениях с добавлением одного “уровня” за раз. Таким образом, алгоритм начинает с s и включает в поиск все узлы, соединенные ребром с s, — так формируется первый уровень поиска. Затем включаются все узлы, соединенные ребром с любым узлом из первого уровня, — второй уровень. Просмотр продолжается до того момента, когда очередная попытка не обнаружит ни одного нового узла.

Если в примере на рис. 3.2 начать с узла 1, первый уровень будет состоять из узлов 2 и 3, второй — из узлов 4, 5, 7 и 8, а третий только из узла 6. На этой стадии поиск останавливается, потому что новых узлов уже не осталось (обратите внимание на то, что узлы 9-13 остаются недостижимыми для поиска).

Как наглядно показывает этот пример, у алгоритма имеется естественная физическая интерпретация. По сути, мы начинаем с узла s и последовательно “затапливаем” граф расширяющейся волной, которая стремится охватить все узлы, которых может достичь. Уровень узла представляет момент времени, в который данный узел будет достигнут при поиске.

Уровни L₁, L₂, L₃, ..., создаваемые алгоритмом BFS, более точно определяются следующим образом:

♦ Уровень L₁ состоит из всех узлов, являющихся соседями s. (Для удобства записи мы иногда будем использовать уровень L₀ для обозначения множества, состоящего только из s.)

♦ Если предположить, что мы определили уровни L₁, ..., L_j, то уровень L_j+1 состоит из всех узлов, не принадлежащих ни одному из предшествующих уровней и соединенных ребром с узлом уровня L_j.

Если вспомнить, что расстояние между двумя узлами определяется как минимальное количество ребер в пути, соединяющем эти узлы, становится понятно, что уровень L₁ представляет собой множество всех узлов, находящихся на расстоянии 1 от s, или в более общей формулировке — уровень L_j представляет собой множество всех узлов, находящихся от s на расстоянии ровно j. Узел не присутствует ни на одном уровне в том, и только в том случае, если пути к нему не существует. Таким образом, алгоритм поиска в ширину определяет не только узлы, достижимые из s, но и вычисляет кратчайшие пути до них. Это свойство алгоритма обобщается в виде следующего факта.

(3.3) Для каждого j ≥ 1 уровень L_j, создаваемый алгоритмом BFS, состоит из всех узлов, находящихся от s на расстоянии ровно j. Путь от s к t существует в том, и только в том случае, если узел t встречается на каком-либо уровне.

Другое свойство поиска в ширину заключается в том, что этот алгоритм естественным образом генерирует дерево T с корнем s, которое состоит из узлов, достижимых из s. А конкретнее, для каждого узла v (отличного от s) рассмотрим момент, когда v впервые “обнаруживается” алгоритмом BFS; это происходит в тот момент, когда проверяется некоторый узел и из уровня L_j и обнаруживается, что из этого узла ребро ведет к узлу v, который не встречался ранее. В этот момент ребро (u, v) добавляется в дерево T — u становится родителем v, представляя тот факт, что и “отвечает” за завершение пути к v. Дерево, построенное таким образом, называется деревом поиска в ширину.

На рис. 3.3 изображен процесс построения дерева BFS с корнем в узле 1 для графа, изображенного на рис. 3.2. Сплошными линиями обозначены ребра T, а пунктирными — ребра G, не принадлежащие T. Ход выполнения алгоритма BFS, приводящего к построению этого дерева, можно описать следующим образом.

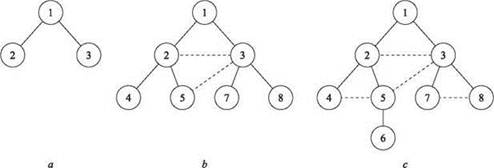
Рис. 3.3. Построение дерева поиска в ширину T для графа на рис. 3.2; фазы (a), (b) и (c) обозначают добавляемые уровни. Сплошными линиями обозначаются ребра T; пунктирные ребра входят в компоненту связности G, содержащую узел 1, но не принадлежащую T

(a) Начиная от узла 1 уровень L₁ состоит из узлов {2, 3}.

(b) Затем для построения уровня L₂ узлы L₁ последовательно проверяются в некотором порядке (допустим, сначала 2, а потом 3). При проверке узла 2 обнаруживаются узлы 4 и 5, поэтому узел 2 становится их родителем. При проверке узла 2 также обнаруживается ребро к узлу 3, но оно не добавляется в дерево BFS, потому что узел 3 нам уже известен.

Узлы 7 и 8 впервые обнаруживаются при проверке узла 3. С другой стороны, ребро от 3-го к 5-му становится еще одним ребром G, которое не включается в T, потому что к моменту обнаружения этого ребра, выходящего из узла 3, узел 5 уже известен.

(c) Затем по порядку проверяются узлы уровня L₂. Единственным новым узлом, обнаруженным при проверке L₂, оказывается узел 6, который добавляется в уровень L₃. Обратите внимание: ребра (4, 5) и (7, 8) не добавляются в дерево BFS, потому что они не приводят к обнаружению новых узлов.

(d) При проверке узла 6 новые узлы не обнаруживаются, поэтому в уровень L₄ ничего не добавляется, и работа алгоритма на этом завершается. Полное дерево BFS изображено на рис. 3.3(c).

Стоит заметить, что при выполнении алгоритма BFS для этого графа ребра, не входящие в дерево, соединяют либо узлы одного уровня, либо узлы смежных уровней. Сейчас мы докажем, что это свойство присуще деревьям BFS вообще.

(3.4) Пусть T — дерево поиска в ширину, x и у — узлы T, принадлежащие уровням L_i и L_j соответственно, а (x, у) — ребро G. В таком случае i и j отличаются не более чем на 1.

Доказательство. Действуя от противного, предположим, что i и j отличаются более чем на 1 — например, что i < j - 1. Рассмотрим точку алгоритма BFS, в которой проверяются ребра, инцидентные х. Так как x принадлежит уровню L_i, то все узлы, обнаруженные от х, принадлежат уровням L_i+1 и менее; следовательно, если у является соседом x, то этот узел должен быть обнаружен к текущему моменту, а это означает, что он должен принадлежать уровню L_i+1 и менее. ■

Связная компонента

Множество узлов, обнаруживаемых алгоритмом BFS, в точности соответствует множеству узлов, достижимых из начального узла s. Это множество R называется компонентой связности G, содержащей s; зная компоненту связности, содержащую s, для ответа на вопрос о связности s-t достаточно проверить, принадлежит ли t компоненте связности.

Если задуматься, становится ясно, что BFS — всего лишь один из возможных способов построения этой компоненты. На более общем уровне компоненту R можно построить “проверкой” G в любом порядке, начиная c s. Сперва определяется R = {s}. Затем в любой момент времени, если удается найти ребро (u, v), для которого u ∈ R и v ∉ R, узел v добавляется в R. В самом деле, если существует путь P из s в u, то существует путь из s в v, который состоит из P с последующим переходом по ребру (u, v). На рис. 3.4 изображен этот базовый шаг расширения компоненты R.

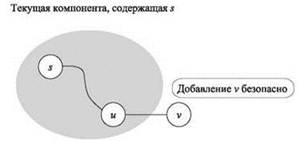
Рис. 3.4. При расширении компоненты связности, содержащей s, мы ищем узлы, которые еще не посещались, такие как v

Предположим, множество R продолжает расти до того момента, пока не останется ни одного ребра, ведущего из R; иначе говоря, выполняется следующий алгоритм.

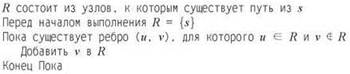
Ниже сформулировано ключевое свойство этого алгоритма.

(3.5) Множество R, построенное в конце выполнения этого алгоритма, в точности совпадает с компонентой связности G, содержащей s.

Доказательство. Ранее уже было показано, что для любого узла v ∈ R существует путь из s в v.

Теперь рассмотрим узел w ∈ R; действуя от обратного, предположим, что в G существует путь s-w, который будет обозначаться P. Так как s ∈ R, но w ∉ R, в пути P должен существовать первый узел v, который не принадлежит R, и этот узел v отличен от s. Следовательно, должен существовать узел u, непосредственно предшествующий v в P, такой что (u, v) является ребром. Более того, поскольку v является первым узлом P, не принадлежащим R, должно выполняться условие u ∈ R. Отсюда следует, что (u, v) — ребро, для которого u ∈ R и v ∉ R; однако это противоречит правилу остановки алгоритма. ■

Заметьте, что для любого узла t в компоненте R можно легко восстановить фактический путь от s к t по описанному выше принципу: для каждого узла v просто фиксируется ребро (u, v), которое рассматривалось на итерации, в которой узел v был добавлен в R. Перемещаясь по этим ребрам в обратном направлении от t, мы обрабатываем серию узлов, добавлявшихся на все более и более ранних итерациях, постепенно достигая s; таким образом определяется путь s-t.

В завершение следует отметить, что общий алгоритм расширения R недостаточно точно определен: как решить, какое ребро должно рассматриваться следующим? Среди прочего, алгоритм BFSпредоставляет способ упорядочения посещаемых узлов — по последовательным уровням, на основании их расстояния от s. Однако существуют и другие естественные способы расширения компоненты, часть из которых ведет к эффективным алгоритмам решения задачи связности с применением поисковых схем, основанных на других структурах. Сейчас мы займемся другим алгоритмом такого рода — поиском в глубину — и изучим некоторые из его базовых свойств.

Поиск в глубину

Другой естественный метод поиска узлов, достижимых из s, естественно применяется в ситуации, когда граф G действительно представляет собой лабиринт из взаимосвязанных комнат. Вы начинаете от s и проверяете первое ребро, ведущее из него, — допустим, к узлу v. Далее вы следуете по первому ребру, выходящему из v, и продолжаете действовать по этой схеме, пока не окажетесь в “тупике” — узле, для которого вы уже исследовали всех соседей. В таком случае вы возвращаетесь к узлу, у которого имеется непроверенный сосед, и продолжаете от него. Этот алгоритм называется алгоритмом поиска в глубину (DFS, Depth-First Search), потому что он продвигается по G на максимально возможную глубину и отступает только по мере необходимости.

Алгоритм DFS также является конкретной реализацией общего алгоритма расширения компоненты, представленного выше. Проще всего описать его в рекурсивной форме: DFS можно запустить от любой начальной точки, но с хранением глобальной информации об уже посещенных узлах.

Чтобы применить его для решения задачи связности s-t, достаточно изначально объявить все узлы “непроверенными” и вызвать DFS(s).

Между алгоритмами DFS и BFS существуют как фундаментальное сходство, так и фундаментальные отличия. Сходство основано на том факте, что оба алгоритма строят компоненту связности, содержащую s, и, как будет показано в следующем разделе, в обоих случаях достигаются сходные уровни эффективности.

Хотя алгоритм DFS в конечном итоге посещает точно те же узлы, что и BFS, обычно посещение происходит в совершенно ином порядке; поиск в глубину проходит по длинным путям и может заходить очень далеко от s, прежде чем вернуться к более близким непроверенным вариантам. Это различие проявляется в том факте, что алгоритм DFS, как и BFS, строит естественное корневое дерево T из компоненты, содержащей s, но обычно такое дерево имеет совершенно иную структуру. Узел s становится корнем дерева T, а узел u становится родителем v, если и отвечает за обнаружение v. А именно, если DFS(v) вызывается непосредственно во время вызова DFS(u), ребро (u, v) добавляется в T. Полученное дерево называется деревом поиска в глубинукомпоненты R.

На рис. 3.5 изображен процесс построения дерева DFS с корнем в узле 1 для графа на рис. 3.2. Сплошными линиями обозначены ребра T, а пунктирными — ребра G, не принадлежащие T. Выполнение алгоритма DFS начинается с построения пути, содержащего узлы 1, 2, 3, 5, 4. Выполнение заходит в тупик в узле 4, в котором найти новые узлы не удается, поэтому алгоритм возвращается к узлу 5, находит узел 6, снова возвращается к 4 и находит узлы 7 и 8. В этой точке в компоненте связности новых узлов нет, поэтому все незавершенные рекурсивные вызовы DFS завершаются один за другим, а выполнение подходит к концу. Полное дерево DFS изображено на рис. 3.5, g.

Этот пример дает представление о внешних отличиях деревьев DFS от деревьев BFS. Такие деревья обычно получаются узкими и глубокими, тогда как для последних характерны минимально короткие пути от корня до листьев. Тем не менее, как и в случае BFS, мы можем выдвинуть достаточно сильное утверждение о расположении ребер G, не входящих в дерево, относительно ребер DFS-дерева T: как и показано на схеме, ребра, не входящие в дерево, могут соединять только предков T с потомками.

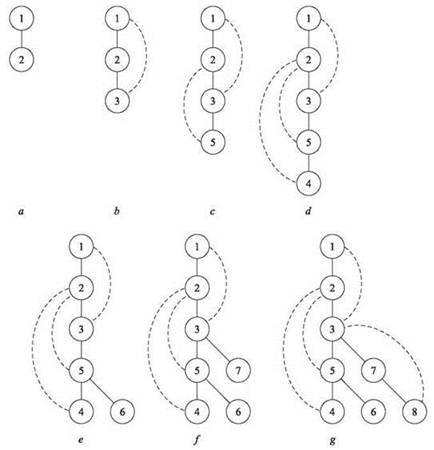
Рис. 3.5. Построение дерева поиска в глубину T для графа на рис. 3.2; фазы (a)-(g) обозначают порядок обнаружения узлов в ходе выполнения. Сплошными линиями обозначены ребра T, а пунктирными — ребра G, не принадлежащие T

Чтобы обосновать это утверждение, следует отметить следующее свойство алгоритма DFS и дерева, которое он строит.

(3.6) Для заданного рекурсивного вызова DFS(u) все узлы, помеченные как “проверенные” между вызовом и концом рекурсивного вызова, являются потомками u в T.

Используя (3.6), мы докажем следующее утверждение:

(3.7) Пусть T — дерево поиска в глубину, x и у — узлы T, а (x, у) — ребро G, которое не является ребром T. В этом случае один из узлов — x или у — является предком другого.

Доказательство. Предположим, (x, у) — ребро G, которое не является ребром T, и без потери общности будем считать, что узел x первым обнаруживается алгоритмом DFS. При проверке ребра (x,у) в ходе выполнения DFS(x) оно не добавляется в T, потому что узел у помечен как “проверенный”. Так как узел у не был помечен как “проверенный” при изначальном вызове DFS(x), этот узел был обнаружен между вызовом и концом рекурсивного вызова DFS(x). Из (3.6) следует, что у является потомком x. ■

Набор всех компонент связности

До настоящего момента мы говорили о компоненте связности, содержащей конкретный узел s. Однако для каждого узла в графе существует своя компонента связности. Какими отношениями связаны эти компоненты?

Как выясняется, эти отношения четко структурированы и описываются следующим утверждением.

(3.8) Для любых двух узлов s и t в графе их компоненты связности либо идентичны, либо не пересекаются.

Это утверждение интуитивно понятно, если взглянуть на граф наподобие изображенного на рис. 3.2. Граф разделен на несколько частей, не соединенных ребрами; самая большая часть — компонента связности узлов 1-8, средняя — компонента связности узлов 11, 12 и 13 и меньшая — компонента связности узлов 9 и 10. Чтобы доказать это общее утверждение, достаточно показать, как точно определяются эти “части” для произвольного графа.

Доказательство. Возьмем любые два узла s и t в графе G, между которыми существует путь. Утверждается, что компоненты связности, содержащие s и t, представляют собой одно и то же множество. Действительно, для любого узла v в компоненте s узел v также должен быть достижим из t через путь: мы можем просто перейти из t в s, а затем из s в v. Аналогичные рассуждения работают при смене ролей s и t, так что узел входит в компоненту одного в том, и только том случае, если он также входит в компоненту другого.

С другой стороны, если пути между s и t не существует, не может быть узла v, входящего в компоненту связности каждого из них. Если бы такой узел v существовал, то мы могли бы перейти от s к v, а затем к t, строя путь между s и t. Следовательно, если пути между s и t не существует, то их компоненты связности изолированы. ■

Из этого доказательства вытекает естественный алгоритм получения всех компонент связности графа, основанный на расширении одной компоненты за раз. Алгоритм начинает с произвольного узла s, а затем использует BFS (или DFS) для генерирования его компоненты связности. Далее мы находим узел v (если он существует), который не был посещен при поиске от s, и итеративным методом, используя BFS от узла v, генерирует компоненту связности — которая, согласно (3.8), изолирована от компоненты s. Это продолжается до тех пор, пока алгоритм не посетит все узлы.