Маршрутизация пакетов - Рандомизированные алгоритмы

Рассмотрим более сложный пример применения рандомизации для снижения конкуренции в распределенных системах, а именно в контексте маршрутизации пакетов.

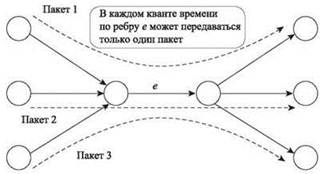
Рис. 13.3. Три пакета, в пути которых входит общее ребро е

Задача

Механизм маршрутизации пакетов обеспечивает передачу данных между узлами большой сети, которая может моделироваться направленным графом G = (V, E). Если узел s захочет передать данные узлу t, эти данные разбиваются на пакеты, каждый из которых передается по сетевому пути s-t P. В любой момент времени в сети может передаваться множество пакетов, связанных с разными источниками и получателями и передаваемых по разным путям. При это действует ключевое ограничение: по каждому ребру e в каждом кванте времени может передаваться только один пакет. Таким образом, когда пакет p прибывает к ребру е, может оказаться, что несколько других пакетов уже ожидают передачи по е; в этом случае p встает в очередь, связанную с ребром е, и ожидает, пока ребро е будет готово передать его. На рис. 13.3, например, три разных пакета с разными источниками и получателями требуют передачи по ребру е; если они поступят к е одновременно, то некоторым из них придется ждать в очереди.

Предположим, имеется сеть G с множеством пакетов, которые должны быть переданы по заданным путям. Нужно понять, сколько шагов понадобится для того, чтобы все пакеты достигли своих получателей. И хотя все пути пакетов полностью известны заранее, мы сталкиваемся с алгоритмической задачей хронометража перемещений пакетов по ребрам. В частности, необходимо решить, когда следует отправить каждый пакет из источника, а также выбрать политику управления очередью для каждого ребра e (то есть как выбирать следующий пакет для передачи из очереди e на каждом шаге).

Важно понимать, что решения по планированию пакетов могут сильно повлиять на время, необходимое для того, чтобы все пакеты добрались до своих получателей. Например, рассмотрим древовидную сеть на рис. 13.4, в которой девять пакетов должны быть переданы по соответствующим пунктирным путям в дереве. Предположим, все пакеты выходят из источников немедленно, и каждое ребро e всегда передает пакет, ближайший к точке получения. В этом случае пакету 1 придется ожидать пакетов 2 и 3 на втором уровне дерева, а позднее — пакетов 6 и 9 на четвертом уровне дерева. Таким образом, для достижения конечной точки пакету потребуется девять шагов. С другой стороны, представим, что каждое ребро e всегда передает пакет, самый дальний от точки получения. Пакету 1 ждать вообще не придется, и он достигнет конечной точки за пять шагов; более того, вы можете убедиться в том, что каждый пакет достигнет своей конечной точки за шесть шагов.

Рис. 13.4. Ситуация, в которой политика управления очередью влияет на время передачи

У древовидной сети на рис. 13.4 существует естественное обобщение, в котором дерево имеет высоту h, а узлы на каждом втором уровне имеют k дочерних узлов. В этом случае с политикой управления очередью, которая всегда передает пакет, ближайший к конечной точке, некоторому пакету потребуется Ω(hk) для завершения передачи (так как пакет, передаваемый на самое дальнее расстояние, задерживается на Ω(k) шагов на каждом из Ω(h) уровней). С другой стороны, с политикой, которая всегда передает пакет, самый дальний от конечной точки, все пакеты достигнут своих конечных точек за O(h + k) шагов. С ростом h и k различия становятся весьма заметными.

Планы и их продолжительность

Перейдем от примеров к теме планирования пакетов и управления очередями в произвольной сети G. Для заданных пакетов 1, 2, ..., N и связанных с ними путей P₁, P₂, ..., P_N план передачи пакетов определяет для каждого ребра e и каждого кванта времени t, какой пакет будет передан по ребру e на шаге t. Конечно, план должен удовлетворять некоторым базовым критериям целостности: за один шаг по любому ребру e передается не более одного пакета, и если пакет i запланирован для передачи по ребру e на шаге t, то ребро e должно входить в путь P_i, и более ранние части плана должны обеспечить достижение e пакетом i. Продолжительностью плана называется количество шагов, необходимых для того, чтобы каждый пакет достиг своей конечной точки; требуется найти план с минимальной продолжительностью.

Что может помешать построению плана с низкой продолжительностью? Одним препятствием может стать очень длинный путь, по которому должен пройти некоторый пакет; очевидно, продолжительность не может быть меньше длины этого пути. Другое потенциальное препятствие — одно ребро e, по которому должны быть переданы многие пакеты; так как каждый из пакетов передается по e на отдельном шаге, это тоже устанавливает нижнюю границу для продолжительности. Итак, для максимальной длины d по множеству путей {P₁, P₂, ..., P_N} и максимальной загрузки c множества путей (максимальное количество путей, имеющих одно общее ребро) продолжительность передачи не может быть меньше mаx(c, d) = Ω(с + d).

В 1988 году Лейтон, Маггс и Рао (Leighton, Maggs, Rao) доказали следующий неожиданный результат: максимальная длина и максимальная загрузка являются единственными препятствиями для поиска быстрых планов — в том смысле, что всегда существует план с продолжительностью O(c + d). Формулировка утверждения очень проста, но доказать его невероятно сложно; и результатом является только очень сложный метод построения такого плана. Вместо того чтобы доказывать это утверждение, мы проанализируем простой алгоритм (также предложенный Лейтоном, Маггсом и Рао), который легко реализуется в распределенной среде и обеспечивает продолжительность, которая отличается в худшую сторону только логарифмическим множителем: O(c + d log(mN)), где m — количество ребер, а N — количество пакетов.

Разработка алгоритма

Простой рандомизированный план

Если каждое ребро просто передает на каждом шаге случайный ожидающий пакет, очевидно, полученный план имеет продолжительность O(cd): в худшем случае пакет может быть заблокирован c - 1 другими пакетами на каждом из d ребер своего пути. Для снижения этой границы необходимо принять меры к тому, чтобы каждый пакет мог проводить в ожидании передачи существенно меньшее количество шагов.

Такая большая граница, как O(cd), может возникнуть из-за очень плохой синхронизации пакетов по отношению друг к другу: блоки из c пакетов одновременно встречаются у одного ребра, а когда “затор” устраняется, то же самое происходит у следующего ребра. Ситуация может показаться аномальной, но следует помнить, что на рис. 13.4 она возникла из-за вполне естественной политики управления очередью. Тем не менее такое нежелательное поведение обусловлено крайне неудачным стечением обстоятельств при синхронизации перемещения пакетов; если ввести в управление пакетами рандомизацию, такое поведение становится маловероятным. Проще всего включить случайный сдвиг по времени выхода пакетов из источника. Даже если через одно ребро должно пройти много пакетов, вряд ли они подойдут одновременно, так как конкуренция за ребра была “сглажена”. Сейчас мы покажем, что такая рандомизация при правильной реализации работает достаточно эффективно.

Для начала рассмотрим следующий алгоритм, который на самом деле не работает. В нем задействован параметр r, значение которого будет определено позднее.

Если случайные задержки действительно будут выбираться так, что никакие два пакета никогда не “столкнутся” (не подойдут к одному ребру одновременно), то этот план будет работать так, как предполагалось; его продолжительность не превысит суммы r (максимальная исходная задержка) и d (максимальное количество ребер по всем путям). Но если r не будет очень большим, где-то в сети может произойти конфликт и в алгоритме произойдет сбой: два пакета одновременно подойдут к ребру e на одном шаге t, и оба должны будут пересечь e на следующем шаге.

Объединение времени в блоки

Чтобы обойти эту проблему, рассмотрим следующее обобщение стратегии: вместо того, чтобы реализовать план “на полной скорости” на уровне отдельных квантов времени, мы реализуем его на уровне смежных блоков квантов.

Этот план будет работать, если удастся избежать более масштабных конфликтов: не должно быть ситуаций, когда более b пакетов должны подойти к одному ребру e в начале одного блока. Если это произойдет, то по крайней мере один из пакетов не сможет быть переданным по e в следующем блоке. Но если исходные задержки обеспечивают распределение, достаточное для того, чтобы к любому ребру в одном блоке прибывали не более b пакетов, то план будет работать так, как задумано. В этом случае продолжительность не превысит b(r + d)-максимального количества блоков r + d, умноженного на длину каждого блока b.

(13.47) Обозначим E событие “более b пакетов должны находиться у одного ребра е в начале одного блока”. Если событие E не происходит, то продолжительность плана не превышает b(r + d).

Наша цель — выбрать значения r и b так, чтобы и вероятность Рr[E], и продолжительность b(r + d) были малыми величинами. Это ключевой момент анализа — если нам удастся продемонстрировать это, то (13.47) даст границу продолжительности.

Анализ алгоритма

Чтобы предоставить границу для Рr[E|, будет полезно разложить это событие на объединение более простых плохих событий для применения границы объединения. Естественное множество плохих событий образуется из раздельного рассмотрения каждого ребра и каждого временного блока: если e — ребро, а t — блок от 1 до r + d, мы обозначим Ф_et, событие “более b пакетов должны быть у ребра е в начале блока i”. Очевидно, Кроме того, если N_et — случайная переменная, равная количеству пакетов, запланированных находиться у ребра е в начале блока t, то событие Ф_et эквивалентно событию [N_et > b].

На следующем шаге анализа случайная переменная N_et раскладывается в сумму независимых случайных переменных, принимающих значения 0 и 1, для применения границы Чернова. Задача естественно решается определением X_eti равным 1, если пакет i должен быть у ребра е в начале блока t, и 0 в противном случае. Тогда и для разных значений i случайные переменные X_eti независимы, так как задержки пакетов выбираются независимо. (Разумеется, X_eti и X_e'_t'_i' с одинаковыми значениями i независимыми не будут; но наш анализ не требует суммирования переменных в этой форме.) Заметим, что из r возможных задержек, которые может выбрать пакет i, не более чем одна потребует его нахождения у ребра е в блоке t; следовательно, E[X_eti] ≤ 1/r. Кроме того, максимум с пакетов имеют пути, включающие е; и если i не входит в их число, то очевидно, E[X_eti] = 0. Следовательно,

Теперь все готово для применения границы Чернова (13.42), так как N_et является суммой независимых случайных переменных X_eti, принимающих значения 0 и 1. Эти величины похожи на те, которые встречались при анализе задачи со случайным распределением m заданий по n процессорам: в том случае каждая составляющая случайная переменная имела ожидание 1/n, общее ожидание было равно m/n и значение m должно было быть равно Ω(n log n), чтобы нагрузка каждого процессора была с высокой вероятностью близка к ожиданию. Подходящая аналогия для текущего случая — r играет роль n, а c играет роль m; во-первых, это выглядит разумно на символическом уровне, с учетом параметров, а во-вторых, соответствует аналогии пакетов с заданиями, а разных временных блоков одного ребра — с разными процессорами, которые могут получать задания. Это наводит на мысль о том, что если мы хотим, чтобы количество пакетов для конкретного ребра в конкретном блоке было близким к ожиданию, то должно выполняться c = Ω(r log r).

Такая аналогия работает, разве что придется немного увеличить логарифмическую составляющую, чтобы в конечном итоге работала граница объединения по всем e и всем t. Итак, назначим

где q — константа, которая будет определена позднее.

Зафиксируем выбор e и t и попробуем ограничить вероятность того, что N_et превышает произведение c/r на константу. Определим μ = c/r и заметим, что E[N_et] ≤ μ, что позволяет применить границу Чернова (13.42). Выберем δ = 2, чтобы и используем как верхнюю границу в выражении Теперь, применяя (13.42), имеем

где z — константа, которую можно сделать сколь угодно большой соответствующим выбором константы q.

Из этих вычислений видно, что будет безопасно присвоить b = 3c/r, потому что в этом случае событие F_et “N_et > b” будет иметь очень малую вероятность для всех вариантов выбора e и t. Всего есть m разных вариантов для e и d + r разных вариантов для t; заметим, что d + r ≤ d + c - 1 ≤ N. Получаем

Из формулы видно, что значение можно сделать сколь угодно малым за счет выбора достаточно большого z.

Из нашего выбора параметров b и r, в сочетании с (13.44), можно сделать следующий вывод:

(13.48) С высокой вероятностью продолжительность плана для пакетов составляет O(c + d log (mN)).

Доказательство. Только что было показано, что вероятность плохого события Е очень мала: она не превышает (mN)^-(z-1) для сколь угодно большой константы z. А при условии, что Е не происходит, (13.47) сообщает, что продолжительность плана ограничивается величиной