Основные вероятностные определения - Рандомизированные алгоритмы

Для многих (хотя, безусловно, не всех) областей применения рандомизированных алгоритмов достаточно работать с вероятностями, определяемыми по конечным множествам; анализировать такие ситуации оказывается намного проще, чем размышлять о вероятностях по произвольным множествам. Итак, для начала мы ограничимся только этим частным случаем, а в конце раздела рассмотрим заново все концепции на более общем уровне.

Конечные вероятностные пространства

Всем нам интуитивно понятны выражения типа “Если подбросить монетку, то “орел” выпадет с вероятностью 1/2” или “При броске кубика вероятность выпадения 6 составляет 1/6”. Начнем с описания математической инфраструктуры, которая позволяет точно анализировать подобные утверждения. Эта инфраструктура хорошо подходит для систем с четко определенными наборами результатов, таких как броски монеток и кубиков; в то же время мы избежим длинных и непростых философских аспектов, возникающих при попытке моделирования утверждений вида “Вероятность того, что завтра пойдет дождь, равна 20 %”. К счастью, в большинстве алгоритмических задач ситуация определяется так же четко, как при бросках кубиков и монеток, — разве что масштабнее и сложнее.

Чтобы иметь возможность вычислять вероятности, введем понятие конечного вероятностного пространства. (Не забывайте, что пока речь идет только о конечных множествах.) Конечное вероятностное пространство определяется нижележащим пространством выборки, которое состоит из всех возможных результатов рассматриваемого процесса. Каждой точке пространства выборки ставится в соответствие неотрицательная вероятностная мераp(i) ≥ 0; единственное ограничение для вероятностных мер заключается в том, что их сумма должна быть равна 1, то есть СобытиеE определяется как произвольное подмножество Ω (то есть просто как множество результатов, образующих это событие), а вероятность события определяется как сумма вероятностных мер всех точек в E, то есть

Во многих ситуациях, которые мы будем рассматривать, все точки пространства выборки имеют одинаковую вероятностную меру, а вероятность события E вычисляется как отношение его размера к размеру Ω; то есть в этом частном случае Pr[E] = |E|/|Ω| Дополняющее событие будет обозначаться Ω—E; заметим, что

Таким образом, точки в пространстве выборки и соответствующие им вероятности образуют полное описание рассматриваемой системы; мы собираемся вычислять вероятности событий — подмножеств пространства выборки. Скажем, для представления одного броска “правильной” монетки можно определить пространство выборки Ω = {heads, tails} и присвоить p(heads) = p(tails) = 1/2. Чтобы смоделировать несимметричную монетку, в которой “орел” выпадает вдвое чаще “решки”, достаточно определить вероятностные меры p(heads) = 2/3 и p(tails) = 1/3. Даже в этом простом примере важно заметить, что определение вероятностных мер является частью задачи; мы указываем, симметрична монетка или нет, при определении условий, а не выводим это из неких дополнительных данных.

Рассмотрим более сложный пример, который можно было бы назвать задачей выбора идентификаторов. Допустим, в распределенной системе существуют n процессов p₁, p₂, ..., p_n, каждый из которых выбирает для себя случайный идентификатор из пространства всех k-разрядных строк. Каждый процесс выбирает свой идентификатор одновременно с другими процессами, поэтому решения принимаются независимо. Если рассматривать каждый идентификатор как элемент, выбираемый из множества {0, 1, 2, ..., 2k - 1} (рассматривая числовое значение идентификатора как число в двоичной записи), пространство выборки Ω можно представить как множество всех n-кортежей целых чисел из диапазона от 0 до 2^k - 1. В этом случае пространство выборки состоит из (2k)n = 2kn точек, каждая из которых имеет вероятностную меру 2^-kn.

Предположим, нас интересует вероятность того, что процессы р₁ и р₂ выберут одинаковые идентификаторы. Это событие E представляется подмножеством, состоящим из всех n-кортежей из Ω с совпадающими первыми двумя координатами. Количество таких n-кортежей равно 2k(n - 1); для координат с 3 по n можно выбрать любое значение, затем для координаты 2 тоже выбирается любое значение, но при выборе координаты 1 свобода полностью отсутствует. Таким образом, получаем

Конечно, это соответствует нашим интуитивным представлениям о вероятности: для процессар₂ можно выбрать любой идентификатор, после чего для процесса р₁ останется всего 1 вариант с совпадением имен из 2^k. Стоит заметить, что эти рассуждения всего лишь компактно описывают приведенные выше вычисления.

Условная вероятность и независимость

Если рассматривать вероятность события E как шанс на то, что событие Е произойдет, также может возникнуть вопрос о его вероятности при наличии дополнительной информации. Для другого события F с положительной вероятностью условная вероятностьE для заданного F определяется как

Это определение также интуитивно понятно, потому что оно ищет ответ на следующий вопрос: какую часть пространства выборки, состоящего из F событие, о наступлении которого нам “известно”), занимает E?

Условные вероятности часто используются при анализе Рr[E] для некоторого сложного события E. Предположим, каждое из событий F₁, F₂, ..., F_k имеет положительную вероятность, и все эти события образуют разбиение пространства выборки; другими словами, каждый результат в пространстве выборки принадлежит ровно одному из них, так что Теперь предположим, что значения Рr[F_j] известны и мы также можем определить Рr[e | F_j] для всех j = 1, 2, ..., k. Следовательно, вероятность события E можно определить в предположении о том, что произошло любое из событий Ф_j. Тогда Рr[E] вычисляется по следующей простой формуле:

Чтобы обосновать эту формулу, развернем ее правую часть:

Независимые события

Два события называются независимыми, если информация об исходе одного из них не влияет на оценку правдоподобия другого. Например, одно из конкретных определений может выглядеть так: события E и F объявляются независимыми, если Рr[E | F] = Рr[E] и Рr[F | E] = Рr[F]. (Будем считать, что оба события имеют положительную вероятность; в противном случае понятие независимости интереса не представляет.) Если выполняется одно из этих двух равенств, то должно выполняться и второе, по следующей причине: если Рr[E | F] = Рr[E], то

а значит, Рr[E ∩ F] = Рr[E] ∙ Pr[F], из чего также следует другое равенство.

Как выясняется, немного проще принять эту эквивалентную формулировку в качестве рабочего определения независимости. Формально события E и F называются независимыми, если Рr[E ∩ F] = Рr[E] ∙ Pr[F].

Формулировка с произведением приводит к следующему естественному обобщению. Совокупность событий Е₁, Е₂, ..., Е_п называется независимой, если для каждого набора индексов I ⊆ {1, 2, ..., n}

Важно заметить следующее: чтобы проверить большое множество событий на независимость, недостаточно убедиться в том, что каждая пара независима. Предположим, мы бросаем три независимые симметричные монетки: если Е_i — событие выпадения “орла” на i-й монетке, то события Е₁, Е₂, Е₃ независимы и каждое из них имеет вероятность 1/2. Теперь обозначим Aсобытие “на монетках 1 и 2 выпали одинаковые значения”; B — событие “на монетках 2 и 3 выпали одинаковые значения”; C — событие “на монетках 1 и 3 выпали разные значения”. Легко убедиться в том, что каждое из этих событий имеет вероятность 1/2, а пересечение любых двух событий имеет вероятность 1/4. Таким образом, любая пара событий, выбранная из A, B, C, независима. При этом множество все трех событий A, B, C независимым не является, так как Pr[A ∩ B ∩ C] = 0.

Граница объединения

Предположим, имеется множество событий Е₁, Е₂, ..., Е_n и нас интересует вероятность наступления каких-либо из этих событий; другими словами, нас интересует вероятность Если все события являются попарно непересекающимися, то вероятностная мера их объединения попросту формируется из отдельных вкладов каждого события.

(13.49) Допустим, имеются события Е₁, Е₂, ..., Е_n, такие что Е_i ∩ Е_j = Ф для каждой пары. Тогда

В общем случае множество событий Е₁, Е₂, ..., Е_n может содержать достаточно сложные перекрытия. В таком случае равенство (13.49) уже не выполняется; из-за перекрытий между событиями вероятностная мера точки, которая учитывается один раз в левой части, будет учтена один или более раз в правой части (рис. 13.5). Это означает, что для общего множества событий равенство в (13.49) ослабляется до неравенства; и этот факт является содержанием границы объединения. Формулировка границы объединения уже приводилась в виде (13.2), но здесь мы приведем ее снова для сравнения с (13.49).

(13.50) (Граница объединения) Для заданных событий Е₁, Е₂, ..., Е_n имеем

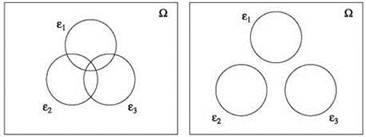
Рис. 13.5. Граница объединения: вероятность объединения максимизируется для неперекрывающихся событий

Несмотря на безобидный внешний вид, граница объединения оказывается неожиданно мощным инструментом для анализа рандомизированных алгоритмов. Ее мощь в основном обусловлена одним часто используемым приемом анализа рандомизированных алгоритмов. Если рандомизированный алгоритм должен выдавать правильный результат с высокой вероятностью, мы сначала определяем множество “плохих событий” Е₁, Е₂, ..., Е_n со следующим свойством: если ни одно из плохих событий не произошло, то алгоритм выдает правильный ответ. Другими словами, если обозначить F событие неудачи при выполнении алгоритма, то

Точно вычислить вероятность объединения сложно, поэтому мы применяем границу объединения и приходим к следующему выводу:

Итак, если алгоритм действительно приводит к успеху с очень высокой вероятностью и плохие события были тщательно выбраны, то каждая из вероятностей Рr[E_i] будет настолько мала, что малой будет даже их сумма (а следовательно, и наша завышенная оценка вероятности неудачи). В этом заключается вся суть происходящего: сложное событие (неудача при выполнении алгоритма) раскладывается на множество простых событий, вероятности которых легко вычисляются.

Простой пример поможет лучше понять рассматриваемую стратегию. Вспомните задачу выбора идентификаторов, описанную ранее в этом разделе, в которой группа процессов пытается выбрать случайный идентификатор. Предположим, в системе существует 1000 процессов, каждый из которых выбирает 32-разрядный идентификатор, и нас интересует вероятность того, что двум процессам будут назначены одинаковые идентификаторы. Можно ли утверждать, что такое стечение обстоятельств маловероятно? Для начала обозначим это событие F. Хотя точно вычислить Рr[F] не так уж и сложно, проще определить границу. Событие F в действительности представляет собой объединение “атомарных” событий; это события Е_ij, в которых процессам р_i и р_j назначаются одинаковые идентификаторы. Легко убедиться в том, что Для любого что было обосновано в одном из предыдущих примеров. Применяя границу объединения, получаем

Значение не больше полумиллиона, а 2³² (немногим более) 4 миллиардов, так что вероятность не превышает

Бесконечные пространства выборки

До сих пор мы имели дело только с конечными вероятностными пространствами. Тем не менее в некоторых разделах этой главы рассматриваются ситуации, в которых случайный процесс может выполняться сколь угодно долго и не может быть нормально описан пространством выборки конечного размера. Для таких ситуаций необходимо определить более общую концепцию вероятностного пространства. Описание содержит много технических подробностей, и отчасти мы приводим его ради полноты: хотя некоторые из рассматриваемых примеров требуют использования бесконечных пространств выборки, ни в одном из них не задействована вся мощь формальных конструкций, описанных в этом разделе.

При переходе к бесконечным пространствам выборки приходится проявлять большую осторожность при определении вероятностной функции. Мы не можем просто связать с каждой точкой пространства выборки Ω вероятностную меру, а затем вычислить вероятность нужной совокупности суммированием. По причинам, в которые мы не будем углубляться, даже если просто разрешить рассматривать каждое подмножество Ω как событие, вероятность которого можно вычислить, это может привести к неприятностям. Обобщенное вероятностное пространство состоит из трех компонентов:

(i) Пространство выборки Ω.

(ii) Набор S подмножеств Ω; только для этих событий разрешено вычисление вероятностей.

(iii) Вероятностная функция Pr, отображающая события из S на вещественные числа из диапазона [0,1].

Совокупность S допустимых событий может быть любым семейством множеств, удовлетворяющим следующим основным свойствам замыканий: пустое множество и полное пространство выборки Ω принадлежат S; если E ∈ S, то (замыкание в отношении дополнения), и если E₁, E₂, E₃, ... ∈ S, то (замыкание в отношении счетного объединения). Вероятностной функцией Prможет быть любая функция из S в [0,1], удовлетворяющая следующим базовым свойствам непротиворечивости: и граница объединения для непересекающихся событий (13.49) должна выполняться даже для счетных объединений — если E₁, E₂, E₃, ... ∈ S являются попарно непересекающимися, то

Так как Pr уже не строится на базе более общего понятия вероятностной меры, (13.49) из теоремы превращается в обязательное свойство Pr.

Как правило, бесконечные пространства выборки возникают в нашем контексте по следующей причине: имеется алгоритм, который принимает серию случайных решений из фиксированного конечного множества возможностей; а поскольку алгоритм может выполняться сколь угодно долго, он может принять произвольно большое количество решений. По этой причине мы рассматриваем пространства выборки Ω, которые строятся следующим образом: мы начинаем с конечного множества символов X = {1, 2, ..., n} и назначаем вес w(i) каждому символу i ∈ X. Затем Ω определяется как множество всех бесконечных последовательностей символов из X (с возможными повторениями). Итак, типичный элемент Ω имеет вид x₁, x₂, х₃, ..., где все х_i ∈ X.

Простейший тип событий, интересующих нас, определяется так: точка ω ∈ Ω начинается с заданной конечной последовательности символов. Таким образом, для конечной последовательности σ = x₁, x₂ ... x_s длины s префиксное событие, связанное с σ, определяется как множество всех точек Ω, для которых первые s символов образуют последовательность σ. Обозначим это событие Е_σи определим его вероятность

Доказать следующий факт определенно нелегко.

(13.51) Существует вероятностное пространство (Ω, S, Pr), удовлетворяющее необходимым условиям замыкания и непротиворечивости, для которого Ω — пространство выборки, определенное выше, E_σ ∈ S для каждой конечной последовательности σ, и

Руководствуясь этим фактом, замыканием S в отношении дополнения и счетного объединения, а также непротиворечивостью Pr в отношении этих операций, мы можем вычислить вероятности практически любого “разумного” подмножества Ω.

В бесконечном пространстве Ω с событиями и вероятностями, определенными так, как показано выше, встречается феномен, не типичный для конечных пространств выборки. Предположим, множество X, используемое для генерирования Ω, равно {0,1}, а w(0) = w(1) = 1/2. Пусть Е — множество, состоящее из всех последовательностей, содержащих как минимум один элемент, равный 1. (Будем считать, что в Е не входит последовательность из одних нулей.) Заметим, что Е является событием в S, так как σ_i можно определить, как последовательность из i - 1 нулей, за которым следует 1, и что Кроме того, все события E_σi являются попарно непересекающимися, поэтому

А теперь феномен, о котором упоминалось выше: событие может иметь вероятность 1 даже в том случае, если оно не равно всему пространству выборки Ω. Аналогичным образом то есть событие может иметь вероятность 0 даже в том случае, если оно не равно пустому множеству. В этих результатах нет ничего странного; в некотором смысле они необходимы, если мы хотим, чтобы вероятности, определяемые на бесконечных множествах, имели смысл. Просто в таких ситуациях необходимо отделять концепцию события с вероятностью 0 от интуитивного представления о том, что событие “невозможно”.