Другие рекуррентные отношения - Разделяй и властвуй

В предыдущем разделе в ходе решения задачи было получено рекуррентное отношение (5.1), которое еще встретится при разработки нескольких алгоритмов типа “разделяй и властвуй” позднее в этой главе. Для дальнейшего исследования этой темы рассмотрим класс рекуррентных отношений, который обобщает (5.1), и посмотрим, как разрешаются рекуррентности из этого класса. Другие представители класса еще встретятся при разработке алгоритмов и в этой, и в последующих главах.

Этот более общий класс алгоритмов образуется при рассмотрении алгоритмов “разделяй и властвуй”, которые создают рекурсивные вызовы для q подзадач с размером n/2 каждая, а затем объединяют результаты за время O(n). Это соответствует рекуррентному отношению сортировки слиянием (5.1) с q = 2 рекурсивных вызовов, или всего одним (q = 1) рекурсивным вызовом. Случай q > 2 встретится позднее в этой главе, когда мы займемся разработкой алгоритмов для целочисленного умножения; разновидность с q = 1 будет представлена позднее, когда мы будем разрабатывать рандомизированный алгоритм нахождения медианы в главе 13.

Если T(n) обозначает время выполнения алгоритма, построенного по такому принципу, то T(n) подчиняется следующему рекуррентному отношению, которое напрямую обобщает (5.1) с заменой 2 на q:

(5.3) Для некоторой константы c,

T(n) ≤ qT(n/2) + cn

для n > 2, и

T(2) ≤ c

В следующем разделе описано, как решить (5.3) с использованием уже применявшихся методов: раскрутки, подстановки и частичной подстановки. Случаи q > 2 и q = 1 рассматриваются по отдельности, так как они качественно отличаются друг от друга, а также от случая q = 2.

Случай q > 2 подзадач

Начнем с раскрутки (5.3) для случая q > 2 по схеме, использованной ранее для (5.1).

Как вы увидите, результат сильно отличается.

♦ Анализ нескольких начальных уровней: пример приведен для случая q = 3 на рис. 5.2. На первом уровне рекурсии имеется одна задача с размером n, которая выполняется за время cn плюс время, потраченное на все последующие рекурсивные вызовы. На следующем уровне имеются q задач с размером n/2. Каждая задача выполняется за время максимум cn/2, что дает в сумме (q/2) cn плюс время последующих рекурсивных вызовов. На следующем уровне используются q² задач с размером n/4 с общим временем (q²/4)cn. Мы видим, что при q > 2 общий объем работы на уровень возрастает с увеличением уровня.

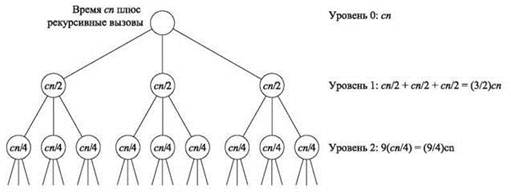
Рис. 5.2. Раскрутка рекуррентности T(n) ≤ 3T(n/2) + O(n)

♦ Выявление закономерности: на произвольном уровне j рекурсии задействованы q^j разных экземпляров, каждый из которых имеет размер n/2^j. Следовательно, общий объем работы, выполняемой на уровне j, составляет q^j(cn/2^j) = (q/2)^jcn.

♦ Суммирование по всем уровням рекурсии: как и в предыдущем случае, существуют log₂ n уровней рекурсии, а общий объем выполняемой работы определяется следующей суммой:

Это геометрическая сумма, состоящая из степеней r = q/2. Воспользовавшись формулой геометрической суммы при r > 1, получаем

Так как нас интересует асимптотическая верхняя граница, будет полезно выделить то, что является константой: последнее выражение может быть записано в виде

Наконец, нужно разобраться в том, что же собой представляет Воспользуемся очень удобной формулой: для всех a > 1 и b > 1 справедливо a^{log b} = b^{log a}. Следовательно,

В итоге получаем

Результат можно обобщить в следующей форме:

(5.4) Любая функция Т(-), удовлетворяющая условию (5.3) c q > 2, имеет границу

Получается, что время выполнения больше линейного, так как log₂ q > 1, но все равно полиномиальное по n. При подстановке конкретных значений q время выполнения составит для q = 3; а для q = 4 оно равно Увеличение времени выполнения с ростом q выглядит логично, поскольку рекурсивные вызовы порождают больший объем работы с увеличением q.

Частичная подстановка

Появление log₂ q в показателе степени естественно следовало из решения (5.3), но такое выражение далеко не всегда можно предположить в исходной ситуации. Посмотрим, как подход, основанный на частичной подстановке, позволяет обнаружить эту экспоненту другим способом.

Допустим, мы предполагаем, что решение (5.3) при q > 2 имеет форму T(n) ≤ kn^d для некоторых констант k > 0 и d > 1. Это достаточно общее предположение, так как мы даже не пытаемся задать показатель степени d. Теперь начнем рассуждения методом индукции и посмотрим, какие ограничения потребуются для k и d. Имеем

В результате применения индукционной гипотезы к T(n/2) это выражение развертывается в

Результат получился поразительно близким: если выбрать d так, чтобы q/2^d = 1, то получится T(n) ≤ kn^d + cn — почти то, что требуется, не считая лишнего члена cn. Итак, нужно разобраться с двумя проблемами: как выбрать d, чтобы q/2^d = 1, и как избавиться от cn.

С выбором d все просто: нужно, чтобы 2^d = q, поэтому d = log₂ q. Как видите, показатель степени log₂ q совершенно естественно появляется, когда мы решаем определить, какое значение dбудет работать при подстановке в рекуррентное отношение.

Но еще нужно избавиться от члена cn. Для этого мы изменим форму предположения для Т(n) так, чтобы явно устранить его вычитанием. Попробуем проверить форму T(n) ≤ kn^d – ln, в которой мы решили, что d = log₂ q, но не зафиксировали константы k или l. При применении новой формулы к T(n/2) получаем

И теперь все полностью работает, если выбрать l так, чтобы другими словами, t = 2c/(q - 2). На этом шаг индукции для n завершается. Также необходимо обработать базовый случай n= 2, а для этого можно воспользоваться тем фактом, что значение k еще не зафиксировано: выберем k достаточно большим, чтобы формула определяла действительную верхнюю границу для случая n = 2.

Случай одной подзадачи

Рассмотрим случай q = 1 в (5.3), который хорошо демонстрирует еще одну разновидность алгоритма. Хотя в этой главе пример применения рекуррентности для q = 1 не встречается, он будет представлен в главе 13, как упоминалось ранее.

Для начала попробуем построить решение методом раскрутки рекуррентного отношения.

♦ Анализ нескольких начальных уровней: начальные уровни рекурсии изображены на рис. 5.3. На первом уровне рекурсии имеется одна задача с размером n, которая выполняется за время сnплюс время, потраченное на все последующие рекурсивные вызовы. На следующем уровне имеется одна задача с размером n/2, которая вносит вклад сn/2; далее идет уровень с одной задачей с размером n/4, добавляющая время сn/4. Как видите, в отличие от предыдущего случая общий объем работы при q = 1 сокращается с ростом уровня рекурсии.

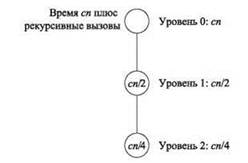
Рис. 5.3. Раскрутка рекуррентности T(n) ≤ T(n/2) + O(n)

♦ Выявление закономерности: на произвольном уровне j по-прежнему остается одна подзадача с размером n/2^j. Ее вклад в общее время выполнения составляет сn/2^j.

♦ Суммирование по всем уровням рекурсии: рекурсия имеет log₂ n уровней, а общий объем выполняемой работы определяется следующей суммой:

Эта геометрическая сумма очень легко вычисляется; даже если продолжить ее до бесконечности, она будет стремиться к 2. Следовательно, выполняется отношение

Т(n) ≤ 2сn = О(n).

Подведем итог:

(5.5) Любая функция T(∙), удовлетворяющая условию (5.3) с q = 1, имеет границу О(n).

На первый взгляд этот результат выглядит противоестественно. Алгоритм выполняет log n уровней рекурсии, но общее время выполнения остается линейным по n. Суть в том, что геометрическая прогрессия с убывающей экспонентой весьма эффективна: половина работы, выполняемой алгоритмом, выполняется на верхнем уровне рекурсии.

Также стоит заметить, что частичная подстановка в рекурсии очень хорошо работает в данном случае. Предположим, как и ранее, что решение задается в форме T(n) ≤ kn^d. Попробуем установить это посредством индукции с использованием (5.3), предполагая, что решение работает для меньшего значения n/2:

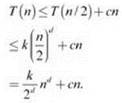
Если теперь просто выбрать d = 1 и k = 2c, получаем

с завершением индукции.

Действие параметра q

Стоит подробнее изучить роль параметра q в классе рекуррентных отношений T(n) ≤ qT(n/2) + O(n), определяемых (5.3). С q = 1 время выполнения получается линейным; с q = 2 оно равно O(n log n); при q > 2 достигается полиномиальная граница с показателем степени больше 1, возрастающим с увеличением q. Причина таких различий во времени выполнения связана с тем, на какой стадии выполняется большая часть работы в этой рекурсии: при q = 1 в общем времени выполнения преобладает верхний уровень, тогда как при q > 2 основная работа выполняется подзадачами постоянного размера на нижних уровнях. Рассматривая происходящее с этой точки зрения, мы видим, что рекуррентное отношение для q = 2 в действительности представляет “баланс”: объем работы, выполняемой на каждом уровне, одинаков для всех уровней, и именно этот фактор обеспечивает время выполнения O(n log n).

Похожее рекуррентное отношение: T(n) ≤ 2T(n/2) + O(n²)

В завершение темы рассмотрим последнее рекуррентное отношение; оно поучительно и как пример убывающей геометрической суммы, и как интересный контраст с рекуррентным отношением (5.1), которым характеризовалась сортировка слиянием. Более того, его разновидность будет рассматриваться в главе 6, когда мы займемся анализом алгоритма “разделяй и властвуй” для решения задачи выравнивания последовательностей с малыми затратами памяти.

Рекуррентное отношение базируется на следующей структуре “разделяй и властвуй”: входные данные разбиваются на два блока равного размера; две подзадачи для этих блоков рекурсивно решаются по отдельности; два результата объединяются в одно решение, с квадратичными затратами времени для исходного деления и итогового объединения.

Для наших целей важно то, что алгоритмы такого рода имеют время выполнения T(n), удовлетворяющее следующему рекуррентному отношению:

(5.6) Для некоторой константы c T(n) ≤ 2T(n/2) + cn² при n > 2, и T(2) ≤ c.

Инстинктивно хочется предположить, что решение будет иметь вид T(n) = O(n² log n), поскольку оно почти идентично (5.1), если не считать увеличения объема работы на уровень с коэффициентом, равным размеру входных данных. На самом деле эта верхняя граница верна (хотя для обоснования потребуются более содержательные обоснования, чем предыдущее предложение), но также выясняется, что верхнюю границу можно усилить. Для этого мы выполним раскрутку рекуррентности по стандартному шаблону.

♦ Анализ нескольких начальных уровней: на первом уровне рекурсии имеется одна задача с размером n, которая выполняется за время cn² плюс время, потраченное на все последующие рекурсивные вызовы. На следующем уровне имеются две задачи с размером n/2. Каждая из них вносит вклад (cn/2)²= cn²/4, что в сумме дает максимум cn²/2, и снова плюс время, потраченное на последующие рекурсивные вызовы. На третьем уровне имеются четыре задачи, каждая из которых имеет размер n/4 и занимает время максимум c(n/4)²= cn²/16, в сумме не более cn²/4. Уже видно, что ситуация отличается от решения для аналогичного рекуррентного отношения (5.1); тогда общий объем работы на уровень оставался неизменным, а здесь он сокращается.

♦ Выявление закономерности: на произвольном уровне j находятся 2^j подзадач, каждая из которых имеет размер п/2^j. Следовательно, общий объем работы на этом уровне ограничивается

♦ Суммирование по всем уровням рекурсии: после всех вычислений мы пришли почти к такой же сумме, которая использовалась для случая q = 1. Получаем

Второе неравенство следует из того факта, что мы имеем дело со сходящейся геометрической суммой.

Оглядываясь назад, видим, что наше исходное предположение T(n) = O(n² log n), базирующееся на аналогии с (5.1), было завышенным из-за скорости убывания составляющей n² при замене ее и т. д. в процессе раскрутки рекуррентного отношения. Из-за этого мы получаем геометрическую сумму вместо суммы, растущей на фиксированную величину по всем n уровням (как в решении (5.1)).