Алгоритмы - Разработка и применение - 2016 год
Упражнения с решениями - Урок 5 - Разделяй и властвуй
Упражнение с решением 1
Имеется массив A из п элементов, в которых хранятся несовпадающие числа. Известно, что последовательность значений A[1], A[2], ..., A[n] унимодальна: для некоторого индекса p в диапазоне от 1 до n значения в элементах массива возрастают до позиции P, а затем убывают до позиции n. (Если нарисовать график, на котором ось x представляет позицию элемента в массиве j, а ось у — значение элемента Aj], график будет возрастать до точки p на оси x, где достигается максимум, а затем будет непрерывно убывать.)
Требуется найти “пиковый элемент” p без чтения всего массива, более того, нужно ограничиться чтением минимально возможного количества элементов A. Покажите, как найтиp чтением не более O(log n) элементов A.
Решение
Сначала обсудим, как вообще добиться времени выполнения O(log n), а затем вернемся к конкретной задаче. Чтобы выполнить некоторые вычисления так, чтобы количество операций не превышало O(log n), можно воспользоваться полезной стратегией, упоминавшейся в главе 2: выполнить постоянный объем работы, отбросить половину входных данных и продолжить рекурсивную обработку остатка. Например, именно эта идея обеспечила время выполнения O(log n) для бинарного поиска.
Происходящее можно рассматривать как проявление принципа “разделяй и властвуй”: для некоторой константы c > 0 выполняются не более c операций, после чего выполнение продолжается рекурсивно для входных данных, размер которых не превышает n/2. Мы будем считать, что рекурсия завершается при n = 2, выполняя максимум c операций для завершения вычислений. Если обозначить T(n) время выполнения для входных данных с размером n, то мы имеем рекуррентное отношение
(5.16) T(n) ≤ T(n/2) + c при n > 2 и T(2) ≤ c.
Это рекуррентное отношение нетрудно разрешить методом раскрутки, как показано ниже.
♦ Анализ нескольких начальных уровней: на первом уровне рекурсии имеется одна задача с размером n, которая выполняется за время c плюс время, потраченное на все последующие рекурсивные вызовы. На следующем уровне имеется одна задача с размером не более n/2, которая добавляет еще c, а на следующем уровне — одна задача с размером не более n/4, добавляющая еще c.
♦ Выявление закономерности: на сколько бы уровней мы ни продолжали анализ, на каждом уровне будет только одна задача: на уровне j будет одна задача с размером не более n/2j, которая вносит вклад c во время выполнения независимо от j.
♦ Суммирование по всем уровням рекурсии: каждый уровень рекурсии добавляет максимум c операций, и для сокращения n до 2 потребуются log2 n уровней рекурсии. Следовательно, общее время выполнения не превышает c, умноженного на количество уровней рекурсии, то есть максимум c log2 n = 0(log n).
К тому же результату также можно прийти частичной подстановкой. Предположим, T(n) ≤ k logb n, причем к и b неизвестны. Если предположить, что это условие выполняется для меньших значений n в индукции, получим
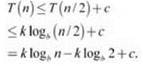
Первое слагаемое в правой части — то, что нам нужно, остается выбрать k и b для компенсации добавления c в конце. Это можно сделать, выбрав b = 2 и k = c, так что k logb 2 = c log2 2 = c. Приходим к решению T(n) ≤ c log n, которое полностью совпадает с тем, которое было получено при раскрутке рекуррентного отношения.
Наконец, стоит упомянуть, что ко времени выполнения O(log n) можно прийти при помощи практически таких же рассуждений в более общем случае, когда на каждом уровне рекурсии отбрасывается любая постоянная часть входных данных, а экземпляр с размером n преобразуется в экземпляр с размером не более an для некоторой константы a < 1. Теперь для сокращения nдо постоянного размера потребуется не более log1/an уровней рекурсии, а каждый уровень рекурсии требует не более c операций.
Вернемся к нашей задаче. Чтобы использовать (5.16), можно было бы проверить среднюю точку массива и попытаться определить, лежит “пиковый элемент” до или после середины.
Допустим, мы обращаемся к значению А[n/2]. По одному этому значению невозможно определить, лежит р до или после n/2, поскольку еще нужно определить, к какой половине относится n/2 — “восходящей” или “нисходящей”. Соответственно мы проверяем значения A[n/2 - 1] и A[n/2 + 1]. Возможны три варианта.
♦ Если A[n/2 - 1] < A[n/2] < A[n/2 + 1], значит, n/2 следует строго перед р, и выполнение можно рекурсивно продолжить для элементов с n/2 + 1 до n.
♦ Если A[n/2 - 1] > A[n/2] > A[n/2 + 1], значит, n/2 следует строго после р, и выполнение можно рекурсивно продолжить для элементов с 1 до n/2 - 1.
♦ Наконец, если A[n/2] больше A[n/2 - 1] и A[n/2 + 1], выполнение завершено: “пиковым элементом” в данном случае является n/2.
Во всех перечисленных случаях выполняется не более трех обращений к массиву А, а задача сводится к задаче с размером не более половинного. Это позволяет применить (5.16) и сделать вывод, что время выполнения составляет O(log n).
Упражнение с решением 2
Вы работаете на небольшую инвестиционную компанию, проводящую интенсивную обработку данных; в вашей работе приходится снова и снова решать задачу определенного типа.
Типичная ситуация выглядит так. Проводится моделирование, при котором рассматриваются курс акций за n последовательных дней где-то в прошлом. Пронумеруем дни i = 1, 2, ..., n; для каждого дня i известна биржевая котировка этих акций p(i) в этот день. (Для простоты будем считать, что в течение дня котировка не изменяется.) Предположим, где-то в этот период времени нужно купить 1000 акций в один день и продать все эти акции в другой (более поздний) день. Вопрос: когда покупать (и когда продавать) акции для получения максимальной прибыли? (Если за эти n дней перепродажа с прибылью невозможна, алгоритм должен сообщить об этом.)
Предположим, n = 3, р(1) = 9, р(2) = 1, р(3) = 5. Алгоритм должен вернуть “Покупать в день 2, продавать в день 3” (в этом случае прибыль составит $4 на акцию — максимально возможная прибыль за этот период).
Очевидно, существует простой алгоритм с временем O(n2): опробовать все возможные комбинации дней покупки/продажи и посмотреть, какой из них обеспечивает максимальную прибыль. Ваши работодатели надеются иметь более эффективное решение.
Покажите, как найти правильные числа i и j за время O(n log n).
Решение
В этой главе уже были рассмотрены примеры, в которых перебор пар элементов методом “грубой силы” сокращается до O(n log n) методом “разделяй и властвуй”. Здесь мы сталкиваемся с аналогичной проблемой — нельзя ли и в этом случае применить стратегию “разделяй и властвуй”?
Было бы естественно рассмотреть первые и последние n/2 дней по отдельности, рекурсивно решить проблему для каждого из этих двух множеств, а затем сформировать из полученных результатов общее решение за время О(n). Тогда можно будет прийти к обычному рекуррентному отношению ![]() а значит, и ко времени O(n log n) согласно (5.1).
а значит, и ко времени O(n log n) согласно (5.1).
Кроме того, для упрощения задачи мы сделаем обычное предположение, что n является степенью 2. Такое предположение не ведет к потере общности: если n' — следующая степень 2 больше n, можно назначить p(i) = p(n) для всех i между n и n'. Ответ при этом не изменится, а размер входных данных в худшем случае увеличится вдвое (что не повлияет на обозначение O()).
Пусть S — множество дней 1, ..., n/2, а S' — множество дней n/2 + 1, ..., n. Наш алгоритм “разделяй и властвуй” базируется на следующем наблюдении: либо существует оптимальное решение, при котором инвесторы удерживают купленные ранее акции в конце дня n/2, либо его не существует. Если решения не существует, то оптимальное решение является лучшим из оптимальных решений множеств S и S'. Если существует оптимальное решение, при котором акции удерживаются в конце дня n/2, то значение этого решения равно p(j) - p(i), где i ∈ S и j ∈ S'. Но это значение максимизируется простым выбором i ∈ S, при котором минимизируется p(i), и выбором j ∈ S', при котором максимизируется p(j).
Следовательно, наш алгоритм должен взять лучшее из трех возможных решений:
♦ Оптимальное решение для S.
♦ Оптимальное решение для S'.
♦ Максимум p( j) - p(i) для i ∈ S и j ∈ S'.
Первые две альтернативы вычисляются за время T(n/2) (каждая посредством рекурсии), а третья альтернатива вычисляется нахождением минимума в S и максимума в S', что выполняется за время O(n). Следовательно, общее время выполнения T(n) удовлетворяет условию ![]() как и требовалось.
как и требовалось.
Стоит заметить, что это не лучшее время выполнения, которое может быть обеспечено в этой задаче. Оптимальную пару дней можно найти за время O(n) средствами динамического программирования (тема следующей главы); а в конце этой главы этот вопрос будет поставлен в упражнении 7.
Упражнения
1. Требуется проанализировать информацию из двух разных баз данных. Каждая база данных содержит n числовых значений (так что общее количество значений равно 2n); будем считать, что одинаковых значений нет. Требуется вычислить медиану этого множества из 2п значений, которую мы определим как n-е значение в порядке возрастания.
Однако доступ к информации затруднен — ее можно получить только при помощи запросов к базам данных. В одном запросе указывается значение k для одной из двух баз данных, и выбранная база данных возвращает k-е значение в порядке возрастания, содержащееся в этой базе. Так как обращения к базам занимают много времени, медиану хотелось бы вычислить с минимальным количеством запросов.
Приведите алгоритм вычисления медианы с количеством запросов не более O(log n).
2. Вспомните задачу нахождения количества инверсий. Как и в тексте главы, дана последовательность чисел а1, ..., an; предполагается, что все числа различны. Определим инверсию как пару i < j, для которой ai > аj.
Также напомним, что задача подсчета инверсий была представлена как способ оценки различий между вариантами упорядочения. Однако кому-то эта метрика может показаться излишне чувствительной. Назовем пару значимой инверсией, если i < j, а аi > 2аj. Приведите алгоритм O(n log n) для подсчета количества значимых инверсий между двумя ранжировками.
3. Вы работаете на банк, который занимается выявлением попыток мошенничества. Поставлена следующая задача: имеется набор из n банковских карт, конфискованных по подозрению в мошенничестве. На каждой банковской карте имеется магнитная полоса с зашифрованными данными, и каждая карта соответствует определенному счету в банке. Две карты называются эквивалентными, если они соответствуют одному счету.
Прочитать номер счета с банковской карты напрямую практически невозможно, но в банке имеется современный аппарат, который берет две банковские карты, и после некоторых вычислений определяет, являются ли они эквивалентными.
Вопрос заключается в следующем: можно ли найти в множестве из n карт подмножество с размером более n/2, эквивалентных друг другу? Считается, что единственной возможной операцией с картами является проверка их на эквивалентность. Покажите, как найти ответ на вопрос так, чтобы количество проверок эквивалентности не превышало O(n log n).
4. Вы работаете в группе физиков, которым при планировании эксперимента требуется проанализировать взаимодействия между очень большим количеством заряженных частиц. По сути, эксперимент проходит так: имеется инертная молекулярная решетка, которая используется для размещения заряженных частиц с равными интервалами по прямой линии. Структура может моделироваться последовательностью точек {1, 2, 3, n} на прямой; в каждой из точек j находится частица с зарядом qj. (Каждый заряд может быть, как положительным, так и отрицательным.)
Физики хотят проанализировать суммарную силу для каждой частицы, измерив ее и сравнив с вычислительным прогнозом. Собственно, именно в вычислительном прогнозе им нужна ваша помощь. Суммарная сила для каждой частицы j по закону Кулона равна
![]()
Для вычисления Fj по всем j написана следующая простая программа:

Нетрудно проанализировать время выполнения этой программы: каждое выполнение внутреннего цикла по i занимает время O(n); этот внутренний цикл вызывается O(n) раз, так что общее время выполнения составляет O(n2).
К сожалению, для больших значений n, с которыми работают физики, эта программа выполняется несколько минут. С другой стороны, экспериментальная установка оптимизирована так, чтобы в нее можно было запустить n частиц, выполнить измерения и приготовиться к обработке новых n частиц за несколько секунд. Физики хотят узнать, нельзя ли вычислить все силы Fj намного быстрее, чтобы не отставать от темпа эксперимента.
Помогите им и разработайте алгоритм, который вычисляет все силы Fj за время O(n log n).
5. Удаление скрытых поверхностей — задача из области компьютерной графики, которая вряд ли нуждается в долгих объяснениях: если Вуди стоит перед Баззом, то вы видите Вуди, а не Базза; если Базз стоит перед Вуди... ну, в общем, вы поняли.
Особенность удаления скрытых поверхностей заключается в том, что часто вычисления производятся намного чаще, чем подсказывает интуиция. Простой геометрический пример демонстрирует суть ускорения. Имеются n невертикальных линий на плоскости L1, ..., Ln, i-я линия определяется уравнением у = aix + bi. Предполагается, что никакие три линии не пересекаются в одной точке. Линия Li будет называться верхней в заданной координате x0, если координата у для точки х0 больше координат у всех остальных линий в точке x0: aix0 + bi > ajx0 + bj для всех j = i. Линия Li называется видимой, если существует координата х, в которой она является верхней (то есть какая-то часть линии видна, если смотреть на нее “сверху вниз” из у = ∞).
Предложите алгоритм, который получает n линий на входе, а за время O(n log n) возвращает все видимые линии. Пример приведен на рис. 5.10.
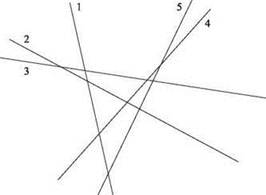
Рис. 5.10. Пример удаления скрытых поверхностей с пятью линиями (помеченными 1-5). Все линии, кроме 2, являются видимыми
6. Рассмотрим полное бинарное дерево T из n узлов, где n = 2d - 1 для некоторого d. Каждый узел v дерева T помечен вещественным числом xv. Считайте, что все вещественные числа различны. Узел v дерева T является локальным минимумом, если метка xv меньше метки xw для всех узлов w, соединенных с v ребром.
Вы получаете полное бинарное дерево T, но метки заданы косвенно: для каждого узла v значение xv определяется проверкой узла v. Покажите, как найти локальный минимум T с использованием только O(log n) проверок узлов T.
7. Предположим, имеется решетчатый граф n х n G. (Решетчатый граф n х n представляет собой граф смежности шахматной доски n х n. Или для полной точности — граф, множество узлов которого является множеством всех упорядоченных пар натуральных чисел (i, j), где 1 ≤ i ≤ n и 1 ≤ j ≤ n; узлы (i, j) и (k, l) соединены ребром в том и только в том случае, если |i - k| + │j - l│ = 1.) Воспользуемся терминологией из предыдущего вопроса. Снова каждый узел v помечается вещественным числом xv; считается, что все метки различны. Покажите, как найти локальный минимум G с использованием только O(n) проверок узлов G. (Обратите внимание: G состоит из n2 узлов.)
Примечания и дополнительная литература
Воинственное выражение “разделяй и властвуй” появилось вскоре после создания самого метода. Кнут (Knuth, 1998) приписывает Джону фон Нейману одно из первых явных выражений этого принципа — алгоритм сортировки слиянием в 1945 году. Также у Кнута (Knuth, 1997b) приведена дополнительная информация о разрешении рекуррентности.
Алгоритм вычисления ближайшей пары точек на плоскости был создан Майклом Шамосом и является одним из первых нетривиальных алгоритмов в области вычислительной геометрии. В обзорной статье Смида (Smid, 1999) обсуждается широкий спектр результатов для задач поиска ближайших точек. Более быстрый рандомизированный алгоритм для этой задачи будет рассмотрен в главе 13. (Смид также делает интересное замечание по поводу неочевидности представленного здесь алгоритма “разделяй и властвуй”: он говорит, что создатели алгоритма изначально считали, что квадратичное время является лучшим возможным для поиска ближайшей пары точек на плоскости.) В более общем плане метод “разделяй и властвуй” оказался очень полезным в вычислительной геометрии, и в книгах Препараты и Шамоса (Preparata, Shamos, 1985) и де Берга и др. (de Berg, 1997) приводится множество других примеров использования этого метода при проектировании геометрических алгоритмов.
Алгоритм умножения двух n-разрядных целых чисел за субквадратичное время разработали Карацуба и Офман (Karatsuba, Ofman, 1962). Дополнительная информация об асимптотически быстрых алгоритмах умножения приводится у Кнута (Knuth, 1997b). Конечно, чтобы субквадратичные методы обеспечили выигрыш по сравнению со стандартным алгоритмом, количество разрядов во входных данных должно быть достаточно большим.
У Пресса и др. (Press et al., 1988) приводится информация о быстром преобразовании Фурье, включая его практическое применение в обработке сигналов и других областях.
Примечания к упражнениям
Упражнение 7 основано на результатах, авторами которых были Донна Луэллин, Крейг Тови и Майкл Трик.