Принципы динамического программирования: мемоизация или итерации с подзадачами - Динамическое программирование

Теперь мы воспользуемся алгоритмом задачи взвешенного интервального планирования, разработанным в предыдущем разделе, для обобщения базовых принципов динамического программирования. Кроме того, он поможет понять принцип, который играет ключевую роль в оставшейся части главы: итерации с подзадачами вместо рекурсивного вычисления решений.

В предыдущем разделе для построения решения задачи взвешенного интервального планирования с полиномиальным временем мы сначала разработали рекурсивный алгоритм с экспоненциальным временем, а затем преобразовали его (посредством мемоизации) в эффективный рекурсивный алгоритм, который обращался к глобальному массиву M за оптимальными решениями подзадач. Но чтобы понять, что здесь на самом деле происходит, желательно сформулировать практически эквивалентную версию алгоритма. Именно эта новая формулировка наиболее явно отражает суть метода динамического программирования и служит общим шаблоном для алгоритмов, которые будут разработаны в последующих разделах.

Разработка алгоритма

Ключом к построению эффективного алгоритма является массив M. В нем закодирована идея о том, что мы используем значение оптимальных решений подзадач для интервалов {1, 2, ..., j} по всем j, и он использует (6.1) для определения значения M[j] на основании значений предшествующих элементов массива. Как только мы получаем массив M, задача решена: M[n] содержит значение оптимального решения для всего экземпляра, а процедура Find-Solution может использоваться для эффективного обратного отслеживания по M и возвращения оптимального решения.

Важно понять, что элементы M можно напрямую вычислять итеративным алгоритмом вместо рекурсии с мемоизацией. Просто начнем с M[0] = 0 и будем увеличивать j; каждый раз, когда потребуется определить значение M[j], ответ предоставляется (6.1). Алгоритм выглядит так:

Анализ алгоритма

Следуя точной аналогии с доказательством (6.3), можно доказать посредством индукции по j, что этот алгоритм записывает OPT(j) в элемент массива M[j]; (6.1) предоставляет шаг индукции. Кроме того, как и ранее, Find-Solution можно передать заполненный массив M для получения оптимального решения помимо значения. Наконец, время выполнения Iterative-Compute-Optочевидно равно O(n), так как алгоритм явно выполняется в течение n итераций и проводит постоянное время в каждой из них.

Пример выполнения Iterative-Compute-Opt представлен на рис. 6.5. При каждой итерации алгоритм заполняет один дополнительный элемент массива M, сравнивая значение v_j + M[p(j)] со значением M[j - 1].

Основная схема динамического программирования

Итак, описанная процедура дает второй эффективный алгоритм решения задачи взвешенного интервального планирования. Разумеется, на концептуальном уровне между двумя решениями существует много общего, поскольку оба решения обусловлены информацией, содержащейся в рекуррентном отношении (6.1). В оставшейся части этой главы мы будем разрабатывать алгоритмы динамического программирования с применением второго метода — итеративного построения подзадач, потому что алгоритмы часто проще выражаются таким образом. Но в каждом из рассматриваемых случаев существует эквивалентная формулировка алгоритма с мемоизированной рекурсией.

Что особенно важно, большую часть нашего обсуждения конкретной задачи выбора интервалов можно преобразовать в заготовку шаблона для разработки алгоритмов динамического программирования. Чтобы взяться за разработку алгоритма, основанного на методе динамического программирования, необходимо иметь набор подзадач, производных от исходной задачи, который обладает некоторыми базовыми свойствами.

(i) Количество подзадач ограничено полиномиальной зависимостью.

(ii) Решение исходной задачи легко вычисляется по решениям подзадач. (Например, исходная задача может быть одной из подзадач.)

(iii) Существует естественное упорядочение подзадач от “меньшей” к “большей” в совокупности с легко вычисляемой рекуррентностью (как в (6.1) и (6.2)), которая позволяет определить решение подзадачи по решениям некоторого количества меньших подзадач.

Естественно, это всего лишь неформальные ориентиры. В частности, понятие “меньшего” из части (iii) зависит от типа рекуррентности.

Вы увидите, что иногда процесс разработки такого алгоритма проще начать с формулировки естественного множества подзадач, а затем найти рекуррентное отношение, которое свяжет их воедино; но часто (как в случае со взвешенным интервальным планированием) полезнее сначала определить рекуррентное отношение на основе анализа структуры оптимального решения, а затем определить, какие подзадачи потребуются для его раскрутки. Связь между подзадачами и рекуррентными отношениями, в которой трудно отделить первопричину от следствия, является одной из тонких особенностей, лежащих в основе динамического программирования. Никогда нельзя быть уверенным в том, что набор подзадач будет полезным, пока не будет найдено рекуррентное отношение, связывающее подзадачи воедино; но о рекуррентном отношении трудно думать в отсутствие “меньших” подзадач, с которыми оно работает. В последующих разделах будут описаны другие приемы, которые помогут справиться с этой неопределенностью.

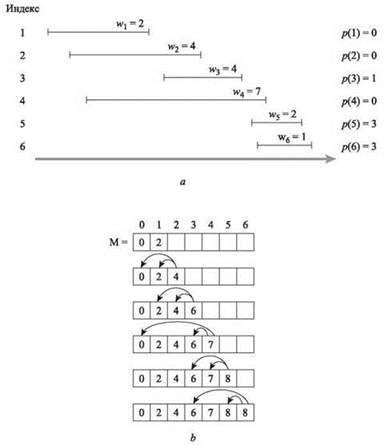
Рис. 6.5. В части b изображены итерации Iterative-Compute-Opt для экземпляра задачи взвешенного интервального планирования (a)