Задача о максимальном потоке и алгоритм Форда-Фалкерсона - Нахождение потока в сети

В этой главе мы займемся семейством алгоритмических задач, которые в каком-то смысле происходят от одной из исходных задач, сформулированных в начале курса: двудольных паросочетаний.

Вспомните исходную формулировку задачи двудольных паросочетаний. Двудольным графом G = (V, E) называется ненаправленный граф, множество узлов которого может быть разбито на подмножества V = X U Y, обладающее тем свойством, что один конец каждого ребра принадлежит X, а другой конец принадлежит Y. Двудольные графы часто изображаются так, как показано на рис. 7.1: узлы X выстраиваются в столбец слева, узлы Y — в столбец справа, а ребра переходят между левым и правым столбцом.

Рис. 7.1. Двудольный граф

Концепция паросочетаний уже неоднократно встречалась в этом учебном курсе: этим термином обозначаются совокупности пар в множествах, в которых ни один элемент множества не входит более чем в одну пару. (Вспомните мужчин и женщин из задачи устойчивых паросочетаний или символы из задачи выравнивания последовательностей.) В случае графа ребра образуют пары узлов, а мы соответственно говорим, что паросочетание в графе G = (V, E) представляет собой множество ребер M ⊆ E с тем свойством, что каждый узел присутствует не более чем в одном ребре M. Множество ребер M является идеальным паросочетанием, если каждый узел присутствует ровно в одном ребре M.

Паросочетания в двудольных графах используются для моделирования ситуаций, в которых одни объекты назначаются другим объектам. Вы уже видели примеры таких ситуаций в предшествующих обсуждениях графов и двудольных графов. В одном из естественных такого рода узлы X представляют задания, узлы Y представляют машины, а ребро (х_i, у_j) означает, что машина у_j способна обработать задание х_i. В этом случае идеальное паросочетание определяет способ распределения заданий между машинами, способными их обработать, при котором каждой машине назначается ровно одно задание. Двудольные графы также могут использоваться для представления других отношений, возникающих между двумя разными множествами объектов: отношений между покупателями и магазинами; домами и обслуживающими их почтовыми отделениями; и т. д.

Задача нахождения наибольшего паросочетания в двудольном графе G относится к числу старейших задач комбинаторных алгоритмов. (Следует заметить, что граф G имеет идеальное паросочетание в том и только в том случае, если |X| = |Y|, и в нем существует паросочетание размера |X|.) Как выясняется, эта задача решается алгоритмом с полиномиальным временем, но разработка такого алгоритма требует применения идей, принципиально отличающихся от приемов, рассматривавшихся нами ранее.

Вместо того чтобы браться за разработку алгоритма напрямую, мы сначала сформулируем общий класс задач — задач нахождения потока в сети, особым случаем которого является задача двудольного паросочетания. Затем мы разработаем алгоритм с полиномиальным временем для общей задачи о максимальном потоке и покажем, как тем самым можно получить эффективный алгоритм для двудольного паросочетания. Хотя изначально задачи потока в сети изучались для анализа трафика в сетях, вы увидите, что они находят широкое применение в самых разных областях и ведут к построению эффективных алгоритмов не только для задачи двудольных паросочетаний, но и для многих других задач.

7.1. Задача о максимальном потоке и алгоритм Форда-Фалкерсона

Графы часто используются для моделирования транспортных сетей — сетей, по ребрам которых передается некоторый трафик, а узлы выполняют функции “пересадочных узлов” для передачи трафика по разным ребрам. Представьте дорожную сеть, в которой ребра представляют дороги, а узлы — развязки; или компьютерную сеть, в которой ребра представляют каналы, способные передавать пакеты, а узлы — коммутаторы; или сеть трубопроводов, в которой ребра представляют трубы, а узлы — места соединения труб. Для сетевых моделей такого типа характерны некоторые компоненты: пропускные способности ребер, обозначающие максимальную величину передаваемого трафика; узлы-источники, генерирующие трафик; узлы-стоки (или приемники), “поглощающие” поступающий трафик; и наконец, сам трафик, передаваемый по ребрам.

Потоковые сети

При рассмотрении графов этого вида трафик называется потоком — это абстрактная сущность, которая генерируется узлами-источниками, передается по ребрам и поглощается узлами-стоками. Формально сеть движения потока (или потоковая сеть) представляет собой направленный граф G = (V, E) со следующими отличительными признаками:

♦ С каждым ребром е связывается пропускная способность — неотрицательное число, которое будет обозначаться c_e.

♦ Существует один узел-источник s ∈ V.

♦ Существует один узел-сток t ∈ V.

Узлы, отличные от s и t, будут называться внутренними узлами.

В отношении потоковых сетей, с которыми мы будем иметь дело, будут действовать два предположения: во-первых, ни одно ребро не входит в источник s, и ни одно ребро не выходит из стока t; во-вторых, у каждого узла существует хотя бы одно инцидентное ему ребро; в-третьих, все пропускные способности представляют собой целые числа. Эти предположения делают модель более стройной и устраняют ряд аномалий, сохраняя практически все интересующие нас свойства.

На рис. 7.2 изображена потоковая сеть с четырьмя узлами и пятью ребрами; рядом с каждым ребром указана его пропускная способность.

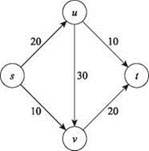
Рис. 7.2. Потоковая сеть с источником s и стоком t. Числа рядом с ребрами обозначают пропускные способности

Определение потока

На следующем шаге мы определим, что же понимается под передачей трафика (или потока) в нашей сети. Поток s-t представляет собой функцию f, которая связывает каждое ребро e с неотрицательным вещественным числом f: E → R⁺; значение f(e) представляет величину потока, передаваемого по ребру е. Поток f должен обладать следующими двумя свойствами¹:

(i) (Ограничения пропускной способности.) Для всех e ∈ E выполняется условие 0 ≤ f(e) ≤ c_e.

(ii) (Ограничения сохранения потока.) Для каждого узла v, отличного от s и t, выполняется условие

Здесь — сумма значений потока по всем ребрам, входящим в узел v, а — сумма значений потока по всем ребрам, выходящим из v.

Таким образом, поток через ребро не может превышать его пропускную способность. Для каждого узла, отличного от источника и стока, величина входного потока должна быть равна величине выходного потока. У источника входящих ребер нет (согласно предположению), но поток из него выходит; иначе говоря, источник генерирует поток. Аналогичным образом сток может иметь входящий поток, хотя у него и нет выходящих ребер. Величина потока f обозначаемая v(f), определяется как сумма потоков, генерируемых в источнике:

Чтобы сделать запись более компактной, мы определим и Определения можно расширить на множества вершин; если S ⊆ V, мы определим и В этой терминологии ограничения сохранения потока для узлов v ≠ s, t принимают вид и мы можем записать

Задача о максимальном потоке

Естественная цель для заданной потоковой сети состоит в организации трафика, обеспечивающей как можно более эффективное использование доступной пропускной способности. Таким образом, основная алгоритмическая задача, которая будет рассматриваться в этой главе, формулируется так: для потоковой сети найти поток максимально возможной величины.

Размышляя над алгоритмом для этой задачи, необходимо учитывать, что структура потоковой сети устанавливает верхние границы для максимальной величины потока s-t. Основное “препятствие” для существования больших потоков заключается в следующем: предположим, узлы графа разделены на два множестваA и B так, что s ∈ A и t ∈ B. Интуитивно ясно, что любой поток, проходящий от s к t, должен в какой-то момент переходить из A в B — а следовательно, заполнять часть пропускной способности ребер из A в B. Из этого следует, что каждый такой “разрез” графа устанавливает ограничение на максимально возможную величину потока. Алгоритм нахождения максимального потока, который мы разработаем в этом разделе, будет объединен с доказательством того, что величина максимального потока равна минимальной пропускной способности любого такого разбиения, называемого минимальным разрезом. Дополнительно наш граф также будет вычислять минимальный разрез. Вы увидите, что задача нахождения разрезов с минимальной пропускной способностью в потоковой сети полезна с точки зрения ее возможных практических применений — например, при нахождении максимального потока.

Разработка алгоритма

Итак, требуется найти максимальный поток в сети. Как взяться за решение этой задачи? Эксперименты показывают, что такие методы, как динамическое программирование, не работают — по крайней мере для задачи о нахождения максимального потока не существует алгоритма, который можно было бы естественно рассматривать как относящийся к парадигме динамического программирования. В отсутствии других идей можно поразмыслить над простыми жадными методами, чтобы понять, почему они не работают.

Допустим, мы начинаем с нулевого потока: f(е) = 0 для всех е. Очевидно, это состояние соблюдает ограничения пропускной способности и сохранения; проблема в том, что в нем величина потока равна 0. Попробуем увеличить значение f, “проталкивая” поток по пути из s в t, до границ, установленных пропускными способностями ребер. Таким образом, на рис. 7.3 можно было бы выбрать путь, состоящий из ребер {(s, u), (u, v), (v, t)}, увеличить поток по каждому из этих ребер до 20 и оставить f(е) = 0 для двух других. Это позволит выполнить ограничения пропускной способности (поток не превышает пропускной способности ребер) и ограничения сохранения потока (при увеличении потока для ребра, входящего во внутренний узел, мы также увеличиваем его для ребра, выходящего из узла). Теперь величина потока равна 20; возникает резонный вопрос: является ли она максимумом, возможным для изображенного графа? Если немного подумать, становится понятно, что в графе можно построить поток с величиной 30. Проблема в том, что мы “зашли в тупик” (не существует пути s-t, в который можно было бы напрямую протолкнуть поток без превышения пропускной способности), а максимальный поток еще не достигнут. Необходим более общий механизм проталкивания потока из s в t, который бы позволял увеличить величину текущего потока в подобных ситуациях.

Фактически нам хотелось бы выполнить операцию, обозначенную на рис. 7.3, c пунктирной линией. В ребро (s, v) проталкиваются 10 единиц потока; в результате в v входит слишком большой поток. Соответственно мы “отменяем” 10 единиц потока в (u, v); при этом восстанавливается ограничение сохранения потока для v, но зато из и выходит слишком малый поток. На последнем шаге 10 единиц потока проталкиваются в ребро (u, t), что приводит к восстановлению состояния сохранения для u. В результате в графе обнаруживается действительный поток величины 30. На рис. 7.3 темными ребрами обозначается поток перед операцией, а пунктирными — возможность его увеличения.

Рис. 7.3. (а) Сеть на рис. 7.2. (b) Проталкивание 20 единиц потока по пути s, u, v, t. (c) Новый увеличивающий путь использует ребро (u, v) в обратном направлении

В этом и заключается более общий механизм проталкивания потока: проталкивание ведется в прямом направлении для ребер со свободной пропускной способностью и в обратном направлении для ребер, по которым уже передается поток, для его перевода в другом направлении. Определим понятие остаточного графа, который предоставит систематический механизм поиска подобных операций.

Остаточный граф

Для заданной потоковой сети G и потока f в G остаточный граф G_f для G в отношении f определяется следующим образом (остаточный граф потока на рис. 7.3 после проталкивания 20 единиц потока по пути s, u, v, t изображен на рис. 7.4):

♦ Множество узлов G_f совпадает с множеством узлов G.

♦ Для каждого ребра e = (u, v) графа G, для которого f(e) < c_e, имеются c_e - f(e) “резервных” единиц пропускной способности, на которые можно попытаться нарастить поток.

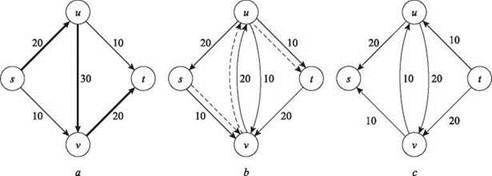
Рис. 7.4. (а) Граф G с путем s, u, v, t используется для проталкивания первых 20 единиц потока. (b) Остаточный граф полученного потока f: рядом с каждым ребром обозначена остаточная пропускная способность. Пунктирная линия обозначает новый увеличивающий путь. (c) Остаточный граф после проталкивания дополнительных 10 единиц потока по новому увеличивающему пути s, u, v, t

Соответственно в G_f включается ребро e = (u, v) с пропускной способностью c_e - f(e). Ребра, включаемые таким образом, называются прямыми ребрами.

♦ Для каждого ребра e = (u, v) графа G, для которого f(e) > 0, имеются f(e) единиц потока, которые можно при необходимости “отменить”, направив поток в обратном направлении. Соответственно в G_f включается ребро e' = (v, u) с пропускной способностью f(e). Заметьте, что e' имеет те же концы, что и e, но проходит в обратном направлении; ребра, включаемые таким образом, называются обратными ребрами.

На этом определение остаточного графа G_f можно считать завершенным. Обратите внимание: каждое ребро e в G может породить одно или два ребра в G_f: если 0 < f(e) < c_e, в G_f включается как прямое, так и обратное ребро. Следовательно, количество ребер в G_f может быть до двух раз больше, чем количество ребер в G. Пропускная способность ребра в остаточном графе иногда называется остаточной пропускной способностью, чтобы ее было проще отличить от пропускной способности соответствующего ребра в исходном потоковом графе G.

Увеличивающие пути в остаточном графе

На следующем шаге мы формализуем способ проталкивания потока из s в t для G_f. Пусть P является простым путем s-t в G_f — иначе говоря, P не посещает ни один узел более одного раза. Определим критическую пропускную способностьbottleneck(P, f) как минимальную остаточную пропускную способность любого ребра P в отношении потока f. Затем определим операцию augment(f, P), которая дает новый поток f' в G.

Собственно, остаточный граф определялся исключительно для того, чтобы мы могли выполнить эту операцию. Любой путь s-t в остаточном графе часто называется увеличивающим путем.

Результат augment(f, P) представляет собой новый поток f' в G, полученный при увеличении и уменьшении величины потока для ребер P. Для начала убедимся в том, что f' действительно является потоком.

(7.1) f' является потоком в графе G.

Доказательство. Необходимо проверить ограничения пропускной способности и сохранения потока. Так как f' отличается от f только на ребрах P, необходимо проверить ограничения пропускной способности только на этих ребрах. Итак, пусть (u, v) — ребро P. Неформально ограничение пропускной способности продолжает выполняться, потому что если e = (u, v) является прямым ребром, мы сознательно предотвращаем увеличение потока на e выше с_e; а если (u, v) является обратным ребром, образовавшимся из ребра e = (v, u) ∈ E, мы сознательно предотвращаем снижение потока через e ниже 0. А если выражаться конкретнее, заметьте, что bottleneck(P, f) не превышает остаточной емкости (u, v). Если e = (u, v) — прямое ребро, то его остаточная пропускная способность равна с_e - f(e); следовательно,

так что ограничение пропускной способности выполняется. Если (u, v) — обратное ребро, образовавшееся из ребра e = (v, u) ∈ E, то его пропускная способность равна f(e), поэтому

и снова ограничение пропускной способности выполняется.

Далее необходимо проверить ограничение сохранения потока для каждого внутреннего узла, лежащего на пути P. Пусть v является таким узлом; нетрудно убедиться в том, что изменение потока, входящего в v, равно изменению потока, выходящего из v; так как f удовлетворяет ограничению сохранения потока в v, для f' оно тоже должно выполняться.

Строго говоря, нужно проверить четыре случая в зависимости от того, является ли ребро P, входящее в v, прямым или обратным ребром, а также является ли ребро P, выходящее из v, прямым или обратным ребром. Однако все эти случаи анализируются достаточно легко, поэтому их проверку мы оставляем читателю. ■

В этой операции увеличения отражены типы прямого и обратного проталкивания потока, о котором говорилось ранее. Рассмотрим следующий алгоритм для вычисления потока s-t в G.

Этот алгоритм называется алгоритмом Форда-Фалкерсона в честь двух ученых, разработавших его в 1956 году. Пример выполнения алгоритма представлен на рис. 7.4. Алгоритм Форда-Фалкерсона в действительности достаточно прост; неочевидно в нем лишь то, завершится ли центральный цикл, и будет ли возвращаемый поток максимальным. Как выясняется, ответы на оба вопроса достаточно нетривиальны.

Анализ алгоритма: завершение и время выполнения

Начнем с доказательства некоторых свойств алгоритма; для этого мы воспользуемся методом индукции по количеству итераций цикла, предполагая, что все пропускные способности являются целыми числами.

(7.2) На каждой промежуточной стадии алгоритма Форда-Фалкерсона величины потока {f(e)} и остаточные пропускные способности в G_f являются целыми числами.

Доказательство. Истинность этого утверждения до начала цикла очевидна. Теперь предположим, что оно истинно после j итераций. Поскольку все остаточные емкости в G_f являются целыми числами, значение bottleneck(P, f) для увеличивающего пути, найденного в итерации j + 1, будет целым числом. Из этого следует, что поток f' будет иметь целые значения — а значит, и пропускные способности нового остаточного графа будут целыми числами. ■

На основании этого свойства можно доказать, что алгоритм Форда-Фалкерсона завершается. Как и ранее в книге, мы будем искать метрику прогресса, из которой можно будет сделать вывод о завершении.

Сначала покажем, что величина потока строго возрастает при применении увеличения.

(7.3) Пусть f — поток в G, а Р — простой путь s-t в G_f. Тогда v(f') = v(f) + bottleneck(P, f); а так как bottleneck(P, f) > 0, имеем v(f') > v(f).

Доказательство. Первое ребро e в пути Р должно выходить из s в остаточном графе G_f; поскольку путь является простым, он не возвращается к s. Так как в G нет ребер, входящих в s, ребро eдолжно быть прямым. Мы увеличиваем поток по этому ребру на bottleneck(P, f) и не изменяем поток через любое другое ребро, инцидентное s. Следовательно, значение f' превышает значение fна bottleneck(P, f). ■

Чтобы доказать завершение цикла, нам потребуется еще одно наблюдение: необходимо иметь возможность установить границу для максимально возможной величины потока. Граница может быть такой: если все ребра, выходящие из s, могут быть полностью насыщены потоком, то величина потока будет равна Обозначим эту сумму C; можно утверждать, что v(f) ≤ C для всех потоков f для s-t. (C как оценка максимальной величины потока в G может быть сильно завышенной, но сейчас она для нас удобна как конечная и просто определяемая граница). Используя утверждение (7.3), мы теперь можем доказать завершение цикла.

(7.4) Предположим, как указано выше, что все пропускные способности в потоковой сети G являются целыми числами. Тогда алгоритм Форда-Фалкерсона завершается не более чем за Cитераций цикла.

Доказательство. Ранее было замечено, что величина никакого потока в G не может превышать C (из-за ограничения пропускной способности для ребер, выходящих из i). Согласно (7.3) величина потока, которым управляет алгоритм Форда-Фалкерсона, возрастает при каждой итерации; следовательно, согласно (7.2), при каждой итерации она увеличивается по крайней мере на 1. Так как значение начинается с 0 и не может превысить C, цикл в алгоритме Форда-Фалкерсона выполняется не более чем за C итераций. ■

Перейдем к рассмотрению времени выполнения алгоритма Форда-Фалкерсона. Пусть n — количество узлов в G, а m — количество ребер в G. Мы предполагали, что все узлы имеют хотя одно инцидентное ребро, поэтому m ≥ n/ 2, и для упрощения границ можно использовать O(m + n) = O(m).

(7.5) Предположим, все пропускные способности в потоковой сети G являются целыми числами. В этом случае алгоритм Форда-Фалкерсона может быть реализован с временем O(mC).

Доказательство. Из (7.4) известно, что алгоритм завершается максимум за C итераций цикла. Рассмотрим объем работы, задействованной в одной итерации при текущем потоке f.

Остаточный граф G_f содержит не более 2m ребер, так как каждое ребро G порождает не более двух ребер в остаточном графе. Для хранения G_f будет использоваться представление списка смежности; для каждого узла v будут храниться два связанных списка: с ребрами, входящими в v, и с ребрами, выходящими из v. Чтобы найти путь s-t в G_f, можно воспользоваться поиском в ширину или в глубину, работающим за время O(m + n); согласно предположению о том, что m ≥ n/2, O(m + n) — то же, что O(m). Процедура augment(f, P) выполняется за время O(n), так как путь P содержит максимум n - 1 ребро. Для известного нового потока f' новый остаточный граф можно построить за время O(m): для каждого ребра e из G строятся правильные ребра (прямое и обратное) в G_f'.

Несколько более эффективная версия алгоритма будет хранить связанные списки ребер остаточного графа G_f в процедуре, изменяющей поток f посредством увеличения.