Алгоритмы - Разработка и применение - 2016 год
Максимальные потоки и минимальные разрезы - Нахождение потока в сети
Перейдем к анализу алгоритма Форда-Фалкерсона, который займет целый раздел. Этот анализ даст много полезной информации не только об алгоритме, но и о задаче о максимальном потоке.
Анализ алгоритма: потоки и разрезы
Наша следующая цель — показать, что поток, возвращаемый алгоритмом Форда-Фалкерсона, имеет максимальную возможную величину для любого потока в G. Для этого мы вернемся к теме, поднятой в разделе 7.1: верхним границам для максимальной величины потока s-t, обусловленным структурой потоковой сети. Одна из таких границ уже приводилась: величина v(f) любого потока s-t не превышает ![]() Иногда эта граница приносит пользу, но иногда оказывается очень слабой. Понятие разреза поможет нам разработать более общий механизм установления верхних границ для величины максимального потока.
Иногда эта граница приносит пользу, но иногда оказывается очень слабой. Понятие разреза поможет нам разработать более общий механизм установления верхних границ для величины максимального потока.
Рассмотрим разбиение узлов графа на два множества A и B, для которых s ∈ A и t ∈ B. Как упоминалось в разделе 7.1, любое такое разбиение устанавливает верхнюю границу для максимально возможного потока, потому что весь поток должен где-то переходить из A в B. Формально разрезомs-t называется разбиение (A, B) множества вершин V, при котором s ∈ A и t ∈ B. Пропускная способность разреза (A, В), которую мы будем обозначать с(А, В), представляет собой обычную сумму пропускных способностей всех ребер, выходящих из А: ![]()
Как выясняется, разрезы устанавливают верхнюю границу для величины потока — очень естественную и хорошо согласующуюся с нашими интуитивными представлениями. Сейчас эти рассуждения будут формализованы в серию фактов.
(7.6) Пусть f — произвольный поток s-t, а (A, В) — произвольный разрез s-t. В этом случае — v(f) = fout(A) – fin(A).
На самом деле это утверждение намного сильнее простой верхней границы. Оно говорит, что по величине потока f, передаваемой через разрез, можно точно измерить величину потока: это общая величина, выходящая из A, за вычетом величины, которая “втекает обратно” в A. Утверждение выглядит вполне естественно, хотя чтобы доказать его, придется немного потрудиться с суммами.
Доказательство. По определению v(f) = fout(s). Из предположения следует fin(s) = 0, так как источник s не имеет входных ребер, и мы можем записать v(f) = fout(s) – fin(s). Кроме s, все узлы v в A являются внутренними, и мы знаем, что fout(v) – fin(v) = 0 для всех таких узлов. Следовательно,
![]()
так как у единственного ненулевого слагаемого в этой сумме v содержит s.
Попробуем переписать правую часть суммы. Если у ребра e оба конца принадлежат A, то f(e) один раз входит в сумму со знаком “+”, и один раз со знаком “-”; эти два слагаемых компенсируются. Если у e в A входит только начальный узел, то f(e) входит в сумму только один раз со знаком “+”. Если у e в A входит только конечный узел, то f(e) входит в сумму только один раз со знаком “-”. Наконец, если у e ни один из концов в A не входит, то f (e) вообще не встречается в сумме. С учетом этого факта имеем
![]()
Объединяя эти два уравнения, приходим к формуле из (7.6). ■
Если A = {s}, то fout(A) = fout(s), и fin(A) = 0, так как по предположению никакие ребра не входят в источник. Следовательно, утверждение для этого множества A = {s} в точности совпадает с определением величины потока v(f).
Для разреза (A, B) ребра, входящие в B, в точности совпадают с ребрами, выходящими из A. Аналогичным образом ребра, выходящие из B, в точности совпадают с ребрами, входящими в A. Следовательно, fout(A) = fin(B) и fin(A) = fout(B) просто из сравнения определений этих двух выражений. Это позволяет переформулировать (7.6) следующим образом:
(7.7) Пусть f — произвольный поток s-t, а (А, В) — произвольный разрез s-t. В этом случае v(f) = fin(B) – fout(B).
Если установить A = V - {t} и B = {t} в (7.7), получаем v(f) = fin(B) - fout(B) = fin(t) - fout(t). По предположению сток не имеет исходящих ребер, поэтому fout(t) = 0. Это означает, что величину потока также можно было бы определить в контексте стока t: это fin(t), величина потока, поступающего в сток.
Очень полезным следствием (7.6) является следующая верхняя граница.
(7.8) Пусть f - любой поток s-t, а (A, B) — любой разрез s-t. В этом случае v(f) ≤ c(A, B).
Доказательство.
![]()
Первая строка — это просто (7.6); переходим от первой строки ко второй, так как fin(A) ≥ 0, а от третьей к четвертой — применяя ограничения пропускной способности к каждому из слагаемых суммы. ■
В некотором смысле утверждение (7.8) выглядит слабее, чем (7.6), так как в нем содержится неравенство вместо равенства. Тем не менее оно чрезвычайно полезно для нас, так как его правая часть не зависит ни от какого конкретного потока f. Фактически (7.8) говорит, что величина любого потока ограничена сверху емкостью любого разреза. Другими словами, рассматривая любой разрез s-t в G с некоторой величиной с* мы немедленно знаем из (7.8), что в G не может быть потока s-t с величиной, превышающей с*. И наоборот, рассматривая любой поток s-t в G с величиной v*, можно сразу утверждать по (7.8), что в s-t не может быть разреза с величиной менее v*.
Анализ алгоритма: максимальный поток равен минимальному разрезу
Обозначим f поток, возвращаемый алгоритмом Форда-Фалкерсона. Требуется показать, что f имеет максимальную возможную величину среди всех потоков в G; для этого мы воспользуемся методом, упоминавшимся выше: предоставим разрез s-t (A*, B*), для которого v(f) = c(A*, B*). Тем самым немедленно устанавливается, что f имеет максимальную величину среди всех потоков и что (A*, B*) имеет минимальную пропускную способность по всем разрезам s-t.
Алгоритм Форда-Фалкерсона завершается, когда поток f не имеет пути s-t в остаточном графе Gf. Как выясняется, это единственное свойство, необходимое для доказательства его максимальности.
(7.9) Если f — такой поток s-t, для которого не существует пути s-t в остаточном графе Gf, то в G существует разрез s-t (A*, B*), для которого v(f) = c(A*, B*). Соответственно f имеет максимальную величину среди всех потоков в G, а (A*, B*) имеет минимальную емкость по всем разрезам s-t в G.
Доказательство. Это утверждение заявляет о существовании разреза, обладающего неким желательным свойством; теперь нужно найти такой разрез. Обозначим A* множество всех узлов v в G, для которых в Gf существует путь s-v. Множество всех остальных узлов обозначается B*: B* = V - A*.
Сначала установим, что (A*, B*) действительно является разрезом s-t. Безусловно, это разбиение V. Источник s принадлежит A*, потому что путь из s в s всегда существует. Кроме того, t ∉ A* по предположению об отсутствии пути s-t в остаточном графе; следовательно, t ∈ B*, как и требуется.
Затем предположим, что e = (u, v) является ребром в G, для которого u ∈ A* и v ∈ B* как показано на рис. 7.5. Можно утверждать, что f(e) = ce. Если бы это было не так, то e было бы прямым ребром в остаточном графе Gf, а поскольку u ∈ A*, в Gf существует путь s-u; присоединяя e к этому пути, мы получаем путь s-v в Gf, что противоречит предположению о v ∈ B*.
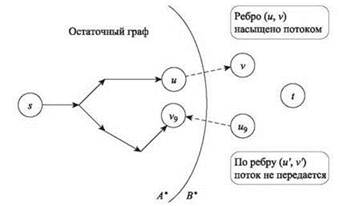
Рис. 7.5. Разрез (A*, B*) в доказательстве (7.9).
Теперь предположим, что e' = (u', v') является ребром в G, для которого u' ∈ B* а v' ∈ A*. Можно утверждать, что f(e') = 0. Если бы это было не так, то ребро e' породило бы обратное ребро e" = (v', u') в остаточном графе Gf, а поскольку v' ∈ A* в Gf существует путь s-v'; присоединяя e" к этому пути, мы получаем путь s-u' в Gf, что противоречит предположению о u' ∈ B*.
Итак, все ребра из A* полностью насыщены потоком, а все ребра, направленные в A*, совершенно не используются. Теперь мы можем воспользоваться (7.6), чтобы прийти к нужному выводу:
![]()
Оглядываясь назад, мы видим, почему два типа остаточных ребер — прямые и обратные — критичны для анализа двух слагаемых в выражении из (7.6).
Так как алгоритм Форда-Фалкерсона завершается при отсутствии пути s-t в остаточном графе, из (7.6) немедленно следует его оптимальность.
(7.10) Поток f возвращаемый алгоритмом Форда-Фалкерсона, является максимальным.
Также заметим, что наш алгоритм легко расширяется для вычисления минимального разреза s-t (A*, B*).
(7.11) Для заданного потока f с максимальной величиной разрез s-t с минимальной пропускной способностью вычисляется за время O(m).
Доказательство. Просто последуем за построением доказательства (7.9). Мы строим остаточный граф Gf и проводим поиск в ширину или поиск в глубину для определения множества A* всех узлов, доступных из s. После этого мы определяем B* = V - A* и возвращаем разрез (A*, B*). ■
Обратите внимание: в графе G может быть много разрезов с минимальной пропускной способностью; процедура в доказательстве (7.11) просто находит один из этих разрезов, начиная с максимального потока f.
Дополнительно анализ алгоритма выявил следующий поразительный факт:
(7.12) В каждой потоковой сети существует поток f и разрез (A, B), для которых v f) = c(A, B).
Суть в том, что f в (7.12) должен быть максимальным потоком s-t; если бы существовал поток f' с большей величиной, то значение f' превысило бы пропускную способность (A, B), а это противоречит (7.8). Аналогичным образом можно сделать вывод о том, что (A, B) в (7.12) является минимальным разрезом (никакой другой разрез не может иметь меньшую пропускную способность), потому что если бы существовал разрез (A', B') с меньшей пропускной способностью, он был бы меньше величины f, а это снова противоречит (7.8). Из-за этих следствий утверждение (7.12) часто называется теоремой о максимальном потоке и минимальном разрезе, и формулируется следующим образом.
(7.13) В любой потоковой сети максимальная величина потока s-t равна минимальной пропускной способности разреза s-t.
Дальнейший анализ: целочисленные потоки
Среди многочисленных следствий нашего анализа алгоритма Форда-Фалкерсона есть одно особенно важное. Согласно (7.2) в любой момент времени величина потока остается целочисленной, а согласно (7.9) в итоге формируется максимальный поток. Следовательно:
(7.14) Если все пропускные способности потоковой сети являются целыми числами, то существует максимальный поток, для которого каждая величина потока f(e) также является целым числом.
Обратите внимание: (7.14) не утверждает, что каждый максимальный поток является целочисленным, а лишь то, что некоторый максимальный поток обладает этим свойством. Интересно, что в (7.14) алгоритм Форда-Фалкерсона никак не упоминается, но наш алгоритмический подход предоставляет, пожалуй, самый простой способ доказательства этого утверждения.
Вещественные числа как пропускные способности
Наконец, прежде чем двигаться дальше, зададимся вопросом, насколько критичным было предположение о целочисленности пропускных способностей (речь не идет о (7.4), (7.5) и (7.14), где оно было очевидно необходимо). Для начала стоит заметить, что если разрешить использование рациональных чисел в качестве пропускных способностей, ситуация не станет более общей, потому что мы можем определить наименьшее общее кратное всех пропускных способностей и умножить их все на это значение, чтобы получить эквивалентную задачу с целочисленными пропускными способностями.
А если пропускные способности будут задаваться вещественными числами? Где в доказательстве мы использовали тот факт, что пропускные способности являются целыми числами? Да, использовали, и он был весьма критичен: утверждение (7.2) использовалось для доказательства того, что в (7.4) величина потока увеличивается по крайней мере на 1 при каждом шаге. С вещественными пропускными способностями следует учесть, что величина потока может возрастать со все более малыми приращениями; следовательно, пропадает гарантия конечности количества итераций цикла. И эта проблема оказывается очень серьезной, потому что при аномальном выборе увеличивающего пути алгоритм Форда-Фалкерсона с вещественными пропускными способностями может выполняться бесконечно.
Однако можно доказать, что теорема о максимальном потоке и минимальном разрезе (7.12) остается истинной даже в том случае, если пропускные способности являются вещественными числами. Утверждение (7.9) предполагало лишь то, что поток f не имеет пути s-t в остаточном графе Gf, чтобы сделать вывод о существовании разреза s-t с равной величиной. Очевидно, для любого потока f с максимальной величиной остаточный граф не содержит пути s-t; в противном случае величину потока можно было бы увеличить. Следовательно, чтобы доказать (7.12) для случая вещественных пропускных способностей, достаточно показать, что в каждой потоковой сети существует максимальный поток.
Конечно, при любом практическом применении потоков пропускные способности будут целыми или вещественными числами. Однако проблема аномального выбора увеличивающего пути может проявиться даже с целыми пропускными способностями: из-за нее алгоритм Форда-Фалкерсона может потребовать огромного количества итераций.
В следующем разделе показано, как выбрать увеличивающие пути так, чтобы избежать потенциально нежелательного поведения алгоритма.