Алгоритмы - Разработка и применение - 2016 год
Алгоритм проталкивания предпотока - Нахождение потока в сети
С самого начала наше обсуждение задачи о максимальном потоке строилось вокруг идеи увеличивающего пути в остаточном графе. Однако существуют и другие эффективные методы нахождения максимального потока, не имеющие прямого отношения к увеличивающим путям. В этом разделе мы рассмотрим один из таких методов: алгоритм проталкивания предпотока.
Разработка алгоритма
Алгоритмы, основанные на увеличивающих путях, хранят состояние потока f и используют процедуру увеличения для наращивания величины потока. С другой стороны, алгоритм проталкивания предпотока по сути увеличивает поток на уровне отдельных ребер. Изменение потока для одного ребра обычно нарушает ограничение сохранения потока, поэтому алгоритм в ходе своей работы должен хранить нечто менее “правильное”, чем поток — нечто, не соблюдающее ограничение сохранения.
Предпотоки
Предпотоком s—t (или сокращенно предпотоком) называется функция f связывающая каждое ребро e с неотрицательным вещественным числом f: E → R+. Предпоток f должен удовлетворять ограничениям пропускной способности:
(i) Для всех e ∈ E выполняется условие 0 ≤ f(e) ≤ ce.
Вместо жестких ограничений сохранения потока обязательны только неравенства: для каждого узла, кроме s, входной поток должен быть по крайней мере не меньше выходного.
(ii) Для всех узлов v, кроме источника s, выполняется условие
![]()
Разность
![]()
называется избыточным потоком предпотока в узле v. Обратите внимание: предпоток, в котором все узлы, кроме s и t, имеют нулевой избыточный поток, является потоком, и величина потока равна в точности ef(t) = -ef(s). Для предпотока f можно определить концепцию остаточного графа Gf — точно так же, как это делалось для потока. Алгоритм “проталкивает” поток по ребрам остаточного графа (с использованием как прямых, так и обратных ребер).
Предпотоки и разметка
Алгоритм проталкивания предпотока работает с предпотоком и стремится преобразовать его в поток. Алгоритм основан на интуитивном представлении о том, что поток естественным образом стекает “сверху вниз”. “Возвышенностями” для этого интуитивного представления являются метки h(v) для всех узлов v, определяемых и поддерживаемых алгоритмом (рис. 7.7). Мы будем проталкивать поток от узлов с большими метками к узлам с меньшими метками (в соответствии с аналогией о жидкости, стекающей сверху вниз). В более точной формулировке разметкапредставляет собой функцию h: V → Z ≥ 0, отображающую узлы на неотрицательные целые числа. Метки также будут называться высотами узлов. Разметка h и предпоток s-t будут называться совместимыми, если
♦ (i) (ограничения источника и стока) h(t) = 0 и h(s) = n,
♦ (ii) (ограничения крутизны) для всех ребер (v, w) ∈ Ef в остаточном графе h(v) ≤ h(w) + 1.
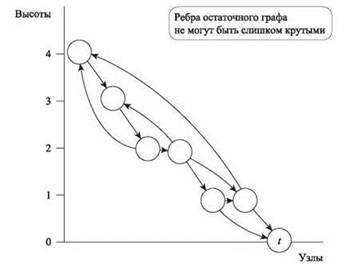
Рис. 7.7. Остаточный граф и совместимая разметка. Никакое ребро в остаточном графе не может быть слишком “крутым” — высота начального узла не может превышать высоту конечного узла более чем на 1. У источника s высота должна быть равна h(s) = n; на схеме она не показана
На уровне здравого смысла понятно: разность высот n между источником и стоком должна гарантировать, что начальная высота достаточна для перетекания потока от s к стоку t, а ограничение крутизны делает его спуск достаточно плавным, чтобы он дошел до стока.
Ключевое свойство совместимого предпотока и разметки заключается в том, что в остаточном графе не может существовать путь s-t.
(7.21) Если предпоток s-t совместим с разметкой h, то в остаточном графе Gf не существует путь s-t.
7.4.* Алгоритм проталкивания предпотока 369
Доказательство. Утверждение доказывается от обратного. Пусть P — простой путь s-t в остаточном графе G. Обозначим узлы P: s, v1, ..., vk = t. По определению разметки, совместимой с предпотоком f, имеем h(s) = n. Ребро (s, v1) входит в остаточный граф, а следовательно, h(v1) ≥ h(s) - 1 = n - 1. Используя индукцию по i и ограничение крутизны для ребра (vi - 1, vi), получаем, что для всех узлов vi в пути P высота равна минимум h(vi) ≥ n - i. Обратите внимание: последним узлом пути является vk = t; следовательно, мы приходим к тому, что h(t) ≥ n - k. Однако h(t) = 0 по определению, а k < n, так как путь P является простым. Это противоречие доказывает исходное утверждение. ■
Вспомните из (7.9), что если в остаточном графе Gf потока f не существует пути s-t, то поток имеет максимальную величину. Из этого вытекает следующее следствие.
(7.22) Если поток s-t совместим с разметкой h, то f является потоком с максимальной величиной.
Следует заметить, что (7.21) относится к предпотокам, а утверждение (7.22) более ограничено в том отношении, что оно применимо только к потокам. Таким образом, алгоритм проталкивания предпотока ведет предпоток f и разметку h, совместимую с f, и работает над модификацией f и h, чтобы превратить f в поток. Когда f действительно станет потоком, мы можем при помощи (7.22) сделать вывод о том, что это поток с максимальной величиной. В свете сказанного алгоритм проталкивания предпотока можно рассматривать как механизм, ортогональный алгоритму Форда-Фалкерсона. Алгоритм Форда-Фалкерсона поддерживает допустимый поток, постепенно изменяя его в направлении оптимальности. Алгоритм проталкивания предпотока, напротив, поддерживает условие, из которого следует оптимальность предпотока f, чтобы он был допустимым потоком, а алгоритм постепенно преобразует предпоток f в поток.
Для запуска алгоритма необходимо определить исходный предпоток f и совместимую с ним разметку h. Мы будем использовать исходную разметку h(v) = 0 для всех v ≠ s, и h(s) = n. Чтобы предпоток f был совместимым с этой разметкой, следует убедиться в том, что ни одно ребро, выходящее из s, не присутствует в остаточном графе (так как эти ребра не удовлетворяют ограничению крутизны). Для этого мы определяем исходный предпоток f(e) = ce для всех ребер e = (s, v), выходящих из источника, и f(e) = 0 для всех остальных ребер.
(7.23) Исходный предпоток f и разметка h совместимы.
Проталкивание и изменение разметки
Теперь посмотрим, какие действия выполняет алгоритм для преобразования предпотока f в допустимый поток, с сохранением его совместимости с некоторой разметкой h. Рассмотрим любой узел v с избыточным потоком (то есть ef(v) > 0). Если в остаточном графе Gf имеется ребро e, которое выходит из v и переходит к узлу w на меньшей высоте (следует учитывать, что h(v) превышает h(w) не более чем на 1 из-за ограничения крутизны), то f можно изменить, перемещая часть избыточного потока из v в w.

Если протолкнуть избыточный поток v по любому ребру, выходящему из v, не удается, значит, необходимо поднять высоту v.
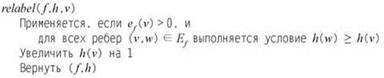
Полный алгоритм проталкивания предпотока
Ниже приведена полная формулировка алгоритма проталкивания предпотока.

Анализ алгоритма
Как обычно, алгоритм нельзя назвать полностью определенным. Для его реализации нужно определить, какой узел с избыточным потоком следует выбрать и как эффективно выбрать ребро для проталкивания. Однако ясно, что каждая итерация этого алгоритма может быть реализована за полиномиальное время. (Позднее мы обсудим, как реализовать ее c достаточной эффективностью.) Более того, нетрудно увидеть, что предпоток f и разметка h остаются совместимыми на протяжении работы алгоритма. Если алгоритм завершается (что из его описания далеко не очевидно), то узлов с положительным избыточным потоком не остается (кроме t), а следовательно, предпоток f действительно является потоком. Затем из (7.22) следует, что f будет максимальным потоком при завершении.
Приведем несколько простых наблюдений относительно алгоритма.
(7.24) Во время выполнения алгоритма проталкивания предпотока:
(i) метки высот являются неотрицательными целыми числами;
(ii) если пропускные способности являются целыми числами, то предпоток f является целым числом;
(iii) предпоток f и разметка h совместимы.
Если алгоритм возвращает предпоток f то f является потоком с максимальной величиной.
Доказательство. Согласно (7.23), исходный предпоток f и разметка h совместимы. Докажем посредством индукции по количеству операций push и relabel, что f и h обладают свойствами из утверждения. Операция проталкивания изменяет предпоток f но границы δ гарантируют, что возвращаемый поток f удовлетворяет ограничениям пропускной способности и что все избыточные потоки остаются неотрицательными, так что f остается предпотоком. Чтобы убедиться в совместимости предпотока f и разметки h, заметим, что операция push(f h, v, w) может добавить одно ребро в остаточный граф — обратное ребро (v, w), и это ребро удовлетворяет ограничению крутизны. Операция relabel увеличивает метку v, а следовательно, повышает крутизну всех ребер, выходящих из v. Однако она применяется только в том случае, если никакое ребро, выходящее из v в остаточном графе, не направлено вниз — а значит, предпоток f и разметка h совместимы после изменения метки.
Алгоритм завершается, когда ни один узел, кроме s или t, не имеет избыточного потока. В этом случае fявляется потоком по определению; а поскольку предпоток f и разметка h остаются совместимыми на протяжении работы алгоритма, из (7.22) следует, что f является потоком с максимальной величиной. ■
Теперь рассмотрим количество операций push и relabel. Сначала докажем ограничение на количество операций relabel — это поможет доказать предел максимального числа возможных операций проталкивания. Алгоритм никогда не изменяет метку s (так как у источника не может быть положительного избыточного потока). У всех остальных узлов v изначально h(v) = 0, а метка возрастает на 1 при каждом изменении. Следовательно, нужно просто установить предел для максимально возможного значения метки. Узел v становится кандидатом для relabel только в том случае, если у v есть избыточный поток. Единственный источником потока в сети является s; интуитивно ясно, что избыточный поток в v должен происходить из s. Следующее следствие из этого факта играет ключевую роль в ограничении меток.
(7.25) Имеется предпоток f. Если в узле v имеется избыточный поток, то существует путь в Gf из v к источнику s.
Доказательство. Пусть A обозначает множество всех узлов w, для которых существует путь из w в s в остаточном графе Gf, а B = V - A. Требуется показать, что все узлы с избыточным потоком принадлежат A.
Отметим, что s ∈ A. Кроме того, никакие ребра e = (х, у), выходящие из A, не могут иметь положительный поток, так как ребро с f(e) > 0 породило бы обратное ребро (y, х) в остаточном графе, и тогда узел у находился бы в A. Теперь рассмотрим сумму избыточных потоков в множестве B и вспомним, что каждый узел в B имеет неотрицательный избыточный поток, так как s ∉ B.
![]()
Изменим запись суммы в правой части. Если оба конца ребра e принадлежат B, то f(e) один раз включается в сумму со знаком “+” и один раз со знаком “-”; два слагаемых компенсируются. Если у e только конечный узел принадлежит B, то e выходит из A, а как было показано выше, у всех ребер, выходящих из A, f(e) = 0. Если у e только начальный узел принадлежит B, то f(e) включается в сумму только один раз со знаком “-”. Таким образом, получаем
![]()
Так как потоки неотрицательны, мы видим, что сумма избыточных потоков в B равна нулю; так как каждый отдельный избыточный поток в B неотрицателен, это означает, что все они должны быть равны 0. ■
Теперь можно доказать, что в процессе выполнения алгоритма метки не изменяются слишком значительно. Вспомните, что n обозначает число узлов в V.
(7.26) Во время выполнения алгоритма для всех узлов h(v) ≤ 2n - 1.
Доказательство. Исходные метки h(t) = 0 и h(s) = n не изменяются во время выполнения алгоритма. Рассмотрим произвольный узел v ≠ s, t. Алгоритм изменяет метку v только при применении операции relabel; пусть f и h — предпоток и разметка, возвращенные операцией relabel (f, h, v). Согласно (7.25) существует путь P в остаточном графе Gf из v в s. Обозначим |P| количество ребер в P; заметим, что |P| ≤ n - 1. Ограничение крутизны подразумевает, что высоты узлов могут убывать не более чем на 1 с каждым ребром P; следовательно, h(v) - h(s) ≤ |P|, что доказывает утверждение. ■
Метки монотонно возрастают во время выполнения алгоритма, поэтому это утверждение немедленно устанавливает предел для количества операций изменения меток.
(7.27) В процессе выполнения алгоритма метка каждого узла изменяется не более 2n - 1 раз, поэтому общее количество операций relabel меньше 2n2.
Затем будет установлена граница для количества операций проталкивания. Будем различать два вида таких операций: операция push(f, h, v, w) называется насыщающей, если либо e = (v, w) является прямым ребром в Еf и δ = ce - f(e), либо (v, w) является обратным ребром с e = (w, v) и δ = f(e). Иначе говоря, проталкивание является насыщающим, если после него ребро (v, w) уходит из остаточного графа. Все остальные операции проталкивания будут называться ненасыщающими.
(7.28) В процессе выполнения алгоритма количество насыщающих операций push не превышает 2nm.
Доказательство. Рассмотрим ребро (v, w) в остаточном графе. После насыщающей операции проталкивания push(f, h, v, w) имеем h(v) = h(w) + 1, а ребро (v, w) покидает остаточный граф Gf, как показано на рис. 7.8. Прежде чем мы снова сможем выполнять проталкивание по этому ребру, сначала необходимо протолкнуть из w в v, чтобы ребро (v, w) появилось в остаточном графе. Но для проталкивания из w в v сначала метка w должна увеличиться минимум на 2 (чтобы узел w находился выше v). Метка w может увеличиться на 2 не более n - 1 раза, так что насыщающее проталкивание из v в w может происходить не более n раз. Каждое ребро e ∈ E может породить до двух ребер в остаточном графе, поэтому общее количество насыщающих проталкиваний не превышает 2nm. ■
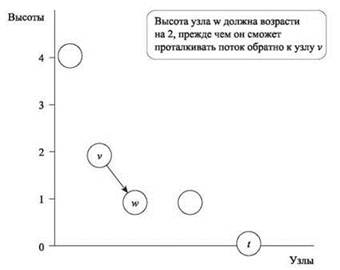
Рис. 7.8. После насыщающего проталкивания push(f, h, v, w) высота v превышает высоту w на 1
Самая сложная часть анализа — доказательство границы для количества ненасыщающих проталкиваний. Она же становится критическим фактором в теоретической границе времени выполнения.
(7.29) В процессе выполнения алгоритма количество ненасыщающих операций push не превышает 2n2m.
Доказательство. В этом доказательстве мы воспользуемся так называемым методом потенциальных функций. Для предпотока f и совместимой разметки h мы определяем
![]()
как сумму высот всех узлов с положительным избыточным потоком. (Функция Ф часто называется потенциальной, потому что она напоминает “потенциальную энергию” всех узлов с положительным избыточным потоком).
В исходном предпотоке и разметке все узлы с положительным избыточным потоком имеют высоту 0, поэтому Ф(f, h) = 0 остается неотрицательной во время выполнения алгоритма. Ненасыщающая операция push(f, h, v, w) уменьшает Ф(f, h) как минимум на 1, потому что после проталкивания узел v не имеет избыточного потока, а w — единственный узел, получающий новый избыточный поток от операции — имеет высоту на 1 меньше, чем v. Однако каждая насыщающая операция проталкивания и каждая операция relabel может увеличить Ф(f, h). Операция relabel увеличивает Ф(f, h) ровно на 1. Выполняется не более 2n2 операций relabel, поэтому общее возрастание Ф(f, h), обусловленное операциями relabel, составит 2n2. Насыщающая операция push(f, h, v, w) не изменяет метки, но она может увеличить Ф(f, h), потому что узел w может неожиданно получить положительный избыточный поток после проталкивания. Это приведет к увеличению Ф(f, h) на высоту w, которая не превышает 2n - 1. Существуют максимум 2nm насыщающих операций проталкивания, поэтому общее возрастание Ф(f, h) из-за операций проталкивания не превышает 2mn(2n - 1). Следовательно, под действием двух факторов Ф(f, h) может возрасти максимум на 4mn2 во время выполнения алгоритма.
Но так как Ф остается неотрицательным и убывает минимум на 1 при каждой ненасыщающей операции проталкивания, из этого следует, что количество ненасыщающих операций проталкивания не может превышать 4mn2. ■
Расширения: улучшенная версия алгоритма
В области правил выбора узлов для улучшения времени выполнения алгоритма проталкивания предпотока в худшем случае были проведены значительные исследования. Сейчас мы рассмотрим простое правило, которое приводит к улучшенной границе O(n3) для количества ненасыщающих операций проталкивания.
(7.30) Если на каждом шаге выбирается узел с избыточным потоком на максимальной высоте, количество ненасыщающих операций проталкивания в процессе выполнения алгоритма не превышает 4n3.
Доказательство. Рассмотрим максимальную высоту ![]() любого узла с избыточным потоком во время выполнения алгоритма. В анализе будет использоваться максимальная высота Н вместо потенциальной функции Ф из предыдущей границы O(n2m).
любого узла с избыточным потоком во время выполнения алгоритма. В анализе будет использоваться максимальная высота Н вместо потенциальной функции Ф из предыдущей границы O(n2m).
Максимальная высота H может увеличиться только из-за изменения меток (так как поток всегда проталкивается к узлам с меньшей высотой), поэтому общее возрастание H в алгоритме не может превышать 2n2 согласно (7.26). Значение H начинается с 0 и остается неотрицательным, поэтому количество изменений H не превышает 4n2.
Теперь рассмотрим поведение алгоритма в фазе времени, в которой H остается постоянной величиной. Утверждается, что каждый узел может иметь максимум одну ненасыщающую операцию push в этой фазе. Действительно, в этой фазе поток проталкивается от узлов на высоте H к узлам на высоте H - 1; и после ненасыщающей операции push от v он должен получить поток от узла на высоте H + 1, прежде чем от него снова можно будет проталкивать поток.
Так как количество ненасыщающих операций push между изменениями H не превышает n, а H изменяется не более 4n2 раз, общее количество ненасыщающих операций push не превышает 4n3. ■
В продолжение (7.30) интересно заметить, что по проведенным экспериментам вычислительным “узким местом” метода является количество операций relabel, и более эффективное время выполнения было получено для модификаций, которые увеличивают метки быстрее, чем по единице. Это обстоятельство будет рассмотрено подробнее в упражнениях.
Реализация алгоритма проталкивания предпотока
Наконец, необходимо кратко обсудить эффективную реализацию этого алгоритма. Несколько простых структур данных позволят эффективно реализовать каждую из операций алгоритма за постоянное время, так что общая реализация алгоритма займет время O(mn) плюс количество ненасыщающих операций push. Следовательно, обобщенный алгоритм будет выполняться за время O(mn2), тогда как версия, которая всегда выбирает узел с максимальной высотой, будет выполняться за время O(n3).
Все узлы с избыточным потоком можно объединить в простой список, чтобы выбор узла с избыточным потоком происходил с постоянным временем. Что касается выбора узла с максимальной высотой H за постоянное время, придется действовать более осмотрительно. Для этого мы будем вести связанный список всех узлов с избыточным потоком на каждой возможной высоте. Обратите внимание: если узел v изменяет метку или сохраняет положительный избыточный поток после проталкивания, он остается узлом с максимальной высотой H. Следовательно, выбирать новый узел после проталкивания нужно только в том случае, когда текущий узел v уже не имеет положительного избыточного потока. Если узел v находился на высоте H, то новый узел на максимальной высоте также будет находиться на высоте H, или если ни один узел на высоте H не имеет избыточного потока, максимальная высота будет равна H - 1, поскольку предыдущая операция push из v протолкнула поток в узел на высоте H - 1.
Теперь предположим, что был выбран узел v и теперь нужно выбрать ребро (v, w) для применения push(f, h, v, w) (или relabel(f, h, v), если такого w не существует). Чтобы иметь возможность быстро выбрать ребро, мы будем использовать представление графа в виде списка смежности. А точнее, для каждого узла v будет вестись связанный список всех возможных ребер, выходящих из v в остаточном графе (как прямых, так и обратных), и с каждым ребром будет храниться его пропускная способность и величина потока. Следует заметить, что в этом случае в структуре данных будут храниться две копии каждого ребра: прямая и обратная. Эти две копии содержат указатели друг на друга, поэтому обновления, выполняемые с одной копией, будут переноситься на другую копию за время O(1). Ребра, выходящие из узла v, будут выбираться для операций push в порядке их следования в списке узла v. Чтобы упростить этот выбор, мы будем поддерживать для каждого узла указатель current(v) на последнее ребро в списке, которое рассматривалось для операции push. Следовательно, если ребро v не имеет избыточного потока после насыщающей операции push из узла v, указатель current(v) останется на этом ребре, и это же ребро будет использоваться для следующей операции push из v. После насыщающей операции push из узла v указатель current(v) перемещается к следующему ребру в списке.
Здесь принципиально то, что после перемещения указателя current(v) от ребра (v, w) операция push не должна повторно применяться к этому ребру, пока не будет изменена метка v.
(7.31) После того, как указатель current(v) переместится от ребра (v, w), применение push к этому ребру невозможно, пока не будет изменена метка v.
Доказательство. После перемещения current(v) от ребра (v, w) вполне логично, что операции push не могут применяться к этому ребру. Либо h(w) ≥ h(v), либо ребро не входит в остаточный граф. В первом случае очевидно, что перед применением push к этому ребру необходимо изменить метку v. Во втором случае необходимо применить push к обратному ребру (w, v), чтобы ребро (v, w) снова вошло в остаточный граф. Однако если применить push к ребру (w, v), то w окажется выше v, а следовательно, метку v необходимо изменить, прежде чем поток можно будет снова проталкивать от v к w. ■
Так как перед изменением метки ребра не нужно снова рассматривать для применения push, приходим к следующему результату.
(7.32) Когда указатель current(v) достигает конца списка ребер для v, к узлу v можно применить операцию relabel.
После изменения метки узла v указатель current(v) возвращается к первому ребру в списке, после чего ребра снова рассматриваются в порядке их следования в списке v.
(7.33) Время выполнения алгоритма проталкивания предпотока, реализованного с использованием описанных структур данных, равно O(mn) плюс O(1) для каждой ненасыщающей операции push. В частности, обобщенный алгоритм проталкивания предпотока выполняется за время 0(n2m), а версия, в которой всегда выбирается узел с максимальной высотой, выполняется за время O(n3).
Доказательство. Исходный поток и процедура изменения меток настраиваются за время O(m). Операции push и relabel (после того, как операция будет выбрана) реализуются за время O(1). Рассмотрим узел v. Мы знаем, что метка v может быть изменена не более 2n раз на протяжении алгоритма. Рассмотрим общее время, потраченное алгоритмом на поиск правильного ребра для проталкивания потока из узла v между двумя изменениями метки v. Если узел v имеет dv смежных ребер, то согласно (7.32) на перемещение указателя current(v) между последовательными изменениями метки v будет потрачено время O(dv). Следовательно, общее время, потраченное на продвижение указателей current, по алгоритму составляет ![]() как и утверждалось. ■
как и утверждалось. ■