Алгоритмы - Разработка и применение - 2016 год
Первое применение: задача о двудольном паросочетании - Нахождение потока в сети
Разработав несколько эффективных алгоритмов для задачи нахождения максимального потока, мы обратимся к практическим применениям максимальных потоков и минимальных разрезов в графах. Начнем с двух фундаментальных задач. В этом разделе рассматривается задача о двудольном паросочетании, упоминавшаяся в начале главы. В следующем разделе мы обратимся к более общей задаче непересекающихся путей.
Задача
Одной из первоначальных целей для разработки алгоритма нахождения максимального потока было решение задачи о двудольном паросочетании; сейчас вы увидите, как это делается. Напомним, что двудольным графомG = (V, E) называется ненаправленный граф, множество узлов которого можно разбить на подмножества V = X U Y, обладающее тем свойством, что один конец каждого ребра e ∈ E принадлежит X, а другой конец принадлежит Y. Паросочетанием M в G называется такое подмножество ребер M ⊆ E, что каждый узел не более чем в одно ребро из M.
Задача о двудольном паросочетании заключается в нахождении в G паросочетания наибольшего возможного размера.
Разработка алгоритма
Граф, определяющий задачу паросочетаний, не направлен, тогда как потоковые сети являются направленными; тем не менее алгоритм задачи нахождения максимального потока легко адаптируется для нахождения максимального паросочетания.
Начиная с графа G в экземпляре задачи о двудольном паросочетании, мы построим потоковую сеть G' так, как показано на рис. 7.9. Сначала все ребра из G будут направлены из X в Y. Затем мы добавим узел s и ребро (s, х) из s в каждый узел X. Далее добавляется узел t и ребро (у, t) из каждого узла из Y в t. Наконец, каждому ребру в G' назначается пропускная способность 1.
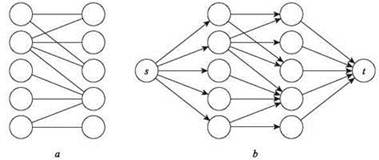
Рис. 7.9. a — двудольный граф; b — соответствующая потоковая сеть, в которой все пропускные способности ребер равны 1
После этого вычисляется максимальный поток s-t в этой сети G'. Как выясняется, величина этого максимального потока равна размеру максимального паросочетания в G. Кроме того, из анализа становится видно, как использовать сам поток для получения паросочетания.
Анализ алгоритма
В основе анализа лежит идея о том, что целочисленные потоки G' достаточно прозрачно кодируют паросочетания из G. Сначала предположим, что в G существует паросочетание, состоящее из k ребер ![]() Затем рассмотрим поток f отправляющий одну единицу потока по каждому пути в форме
Затем рассмотрим поток f отправляющий одну единицу потока по каждому пути в форме ![]() — то есть f(e) = 1 для каждого ребра на одном из этих путей. Легко убедиться в том, что ограничения пропускной способности и сохранения потока действительно выполняются, а f является потоком s-t с величиной k.
— то есть f(e) = 1 для каждого ребра на одном из этих путей. Легко убедиться в том, что ограничения пропускной способности и сохранения потока действительно выполняются, а f является потоком s-t с величиной k.
И наоборот, предположим, что в G' существует поток f' с величиной k. Согласно теореме целочисленности максимальных потоков известно, что существует целочисленный поток f с величиной k; а поскольку все пропускные способности равны 1, это означает, что для каждого ребра e значение f(e) равно 0 или 1. Теперь рассмотрим множество М' всех ребер в форме (x, y), для которых величина потока равна 1.
Множество M' обладает тремя простыми свойствами.
(7.34) M' состоит из k ребер.
Доказательство. Чтобы доказать это утверждение, рассмотрим разрез (A, B) в G' c A = {s} U X. Величина потока вычисляется как общий поток, выходящий из A, за вычетом общего потока, входящего в A. Первое из этих слагаемых попросту равно мощности M', так как ребра, выходящие из A, несут поток, причем каждое ребро несет ровно одну единицу потока. Второе слагаемое равно 0, так как в A нет входящих ребер. Из этого следует, что M' содержит к ребер. ■
(7.35) Каждый узел в X является начальным не более чем для одного ребра в M' .
Доказательство. Чтобы доказать это утверждение, предположим, что x ∈ X является начальным узлом для минимум двух ребер в M'. Так как поток является целочисленным, это означает, что из x выходят как минимум две единицы потока. По ограничению сохранения потока в x должны входить минимум две единицы потока — но это невозможно, поскольку в x входит только одно ребро с пропускной способностью 1. А следовательно, x является начальным узлом не более чем для одного ребра в M'.
Рассуждая аналогичным образом, можно показать, что
(7.36) Каждый узел в Y является конечным не более чем для одного ребра в M'. Объединяя все эти свойства, мы видим, что при рассмотрении M' как множества ребер в исходном двудольном графе G будет получено паросочетание с размером k. В итоге нам удалось доказать следующий факт.
(7.37) Размер максимального паросочетания в G равен величине максимального потока в G'; а ребрами такого паросочетания в G являются ребра, передающие поток от X к Y в G'.
Обратите внимание на важную роль, отведенную теореме целочисленности (7.14) в этом построении: мы должны были знать, существует ли в G' максимальный поток, состоящий только из величин 0 и 1.
Граница времени выполнения
Теперь посмотрим, насколько быстро можно вычислить максимальное паросочетание в G. Пусть n = X = |Y|, а m — количество ребер в G. Будем предполагать, что существует хотя бы одно ребро, инцидентное каждому узлу из исходной задачи — а следовательно, m ≥ n/2. Во времени вычисления максимального паросочетания доминирующим фактором является время вычисления целочисленного максимального потока в G', так как преобразование его в паросочетание в G выполняется просто. Для этой задачи потока имеем ![]() так как s содержит ребро с пропускной способностью 1 для каждого узла X. Используя границу O(mC) из (7.5), получаем:
так как s содержит ребро с пропускной способностью 1 для каждого узла X. Используя границу O(mC) из (7.5), получаем:
(7.38) Алгоритм Форда-Фалкерсона может использоваться для нахождения максимального паросочетания в двудольном графе за время O(mn).
Интересно, что при использовании “улучшенных” границ O(m2 log2 C) или O(n3), разработанных в предыдущих разделах, мы бы получили для этой задачи ухудшенное время O(m2 log n) или O(n3). В этом нет никакого противоречия. Эти границы проектировались как хорошие для любых ситуаций, даже при очень больших C относительно m и n. Но для задачи о двудольном паросочетании C = n, так что затраты, связанные с усложнением, в этом случае оказываются излишними.
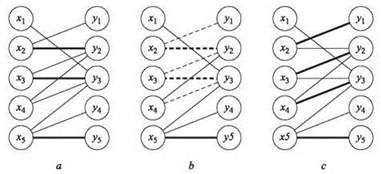
Рис. 7.10. a — двудольный граф с паросочетанием M; b — увеличивающий путь в соответствующем остаточном графе; c — паросочетание, полученное в результате увеличения
Также стоит задуматься над смыслом улучшающих путей в сети G'. Рассмотрим паросочетание M, состоящее из ребер (x2, y2), (x3, y3) и (x5, y5) в двудольном графе на рис. 7.1 (также см. рис. 7.10). Обозначим f соответствующий поток в G'. Это паросочетание не является максимальным, поэтому f не является максимальным потоком s-t, а следовательно, существует увеличивающий путь в остаточном графе Gf'. Один из таких увеличивающих путей помечен на рис. 7.10, b. Обратите внимание: ребра (x2, у2) и (x3, у3) используются в обратном направлении, а все остальные ребра — в прямом. Все увеличивающие пути должны чередоваться между ребрами, используемыми в обратном и прямом направлении, так как все ребра графа G' переходят из X в Y. По этой причине в контексте поиска максимального паросочетания увеличивающие пути называются чередующимися путями. Увеличение направлено на то, чтобы вывести из паросочетания ребра, идущие в обратном направлении, и заменить их ребрами, идущими в прямом направлении. Так как увеличивающий путь идет от s к t, прямых ребер на 1 больше, чем обратных; следовательно, размер паросочетания увеличивается на 1.
Расширения: структура двудольных графов без идеального паросочетания
С алгоритмической точки зрения мы уже знаем, как найти идеальное паросочетание: нужно использовать приведенный выше алгоритм для нахождения максимального паросочетания, а потом проверить, является ли это паросочетание идеальным.
Но пока зададимся чуть менее алгоритмическим вопросом. Не во всех двудольных графах существуют идеальные паросочетания. Как выглядит двудольный граф без идеального паросочетания? Существует ли простой способ определить, что двудольный граф не имеет идеального паросочетания — или по крайней мере убедить кого-то в том, что граф не имеет идеального паросочетания, после выполнения алгоритма? А если говорить конкретнее, было бы хорошо, если бы алгоритм после принятия решения об отсутствии идеального паросочетания мог выдать короткий “сертификат”, подтверждающий его отсутствие. С таким сертификатом любой желающий мог бы быстро убедиться в отсутствии идеального паросочетания без отслеживания всего хода выполнения алгоритма.
Чтобы понять идею такого сертификата, на происходящее можно было бы взглянуть так, чтобы решить, имеет ли граф G идеальное паросочетание, мы могли бы проверить, что величина максимального потока в графе G' не ниже n. Согласно теореме о максимальном потоке и минимальном разрезе, разрез s-t с пропускной способностью ниже n существует в том случае, если величина максимального потока в G' ниже n. Итак, разрез с пропускной способностью ниже n мог бы послужить таким сертификатом. Однако нам нужен сертификат, обладающий естественным смыслом в контексте исходного графа G.
Как мог бы выглядеть такой сертификат? Например, если существуют узлы x1, x2 ∈ X, каждый из которых имеет только одно инцидентное ребро, а другим концом каждого ребра является один и тот же узел у, очевидно, такой граф не имеет идеального паросочетания: и x1 и x2 должны будут оказаться в паре с одним узлом у. На более общем уровне рассмотрим подмножество узлов A ⊆X; пусть Г(А) ⊆ Y обозначает множество всех узлов, смежных с узлами в A. Если граф имеет идеальное паросочетание, то все узлы в А должен находиться в парах с разными узлами в Г(А), так что множество Г(А) должно быть по крайней мере не меньше A. Мы приходим к следующему факту.
(7.39) Если двудольный граф G = (V, E) с двумя сторонами X и Y имеет идеальное паросочетание, то для всех А ⊆ X должно выполняться условие |Г(А)| ≥ |А|.
Это утверждение подсказывает, какой сертификат мог бы демонстрировать отсутствие идеального паросочетания у графа: множество А ⊆ X, для которого |Г(А)| < |А|. Но будет ли истинным также условие, обратное (7.39)? Действительно ли в любой ситуации при отсутствии идеального паросочетания существует подобное множество А, которое это доказывает? Ответ на этот вопрос оказывается положительным, если добавить очевидное условие |X| = |Y| (без которого идеального паросочетания, конечно, быть не может). Это утверждение известно в литературе как теорема Холла, хотя его разновидности были независимо открыты несколькими учеными (вероятно, первым был Кёниг) в начале 1900-х годов. Из доказательства утверждения также вытекает способ нахождения такого подмножества А за полиномиальное время.
(7.40) Предположим, в двудольном графе G = (V, E) имеются две стороны X и Y, для которых |X| = |Y|. В этом случае граф G либо имеет идеальное паросочетание, либо существует такое подмножество А ⊆ X, что |Г(А)| < |А|. Идеальное паросочетание или соответствующее подмножество А могут быть найдены за время O(mn).
Доказательство. Воспользуемся тем же графом G', что и в (7.37). Будем считать, что |X| = |Y| = n. Согласно (7.37) граф G имеет максимальное паросочетание в том и только в том случае, если величина максимального потока в G' равна n.
Необходимо показать, что если величина максимального потока меньше n, то существует подмножество А, для которого |Г(А)| < |А|, как указано в утверждении. По теореме о максимальном потоке и минимально разрезе (7.12), если величина максимального потока меньше n, то существует разрез (А', B') с пропускной способностью менее n в G'. Множество А' содержит s, и может содержать узлы как из X, так и из Y, как показано на рис. 7.11. Утверждается, что множество А = X ∩ А' обладает заявленным свойством. Если нам удастся это доказать, то тем самым будут доказаны обе части утверждения, так как в (7.11) было показано, что минимальный разрез (А', B') также может быть найден выполнением алгоритма Форда-Фалкерсона.
Начнем с того, что минимальный разрез (А', B') можно изменить так, чтобы гарантировать выполнение условия Г(А) ⊆ А'(как и прежде, А = X ∩ А'). Для этого рассмотрим узел у ∈ Г(А), принадлежащий B', как показано на рис. 7.11, а. Утверждается, что перемещение у из B' в А' не увеличивает емкость разреза. Действительно, что происходит при перемещении у из B' в А'? Ребро (у, t) теперь пересекает разрез, увеличивая пропускную способность на 1. Но ранее было по крайней мере одно ребро (x, у) с x ∈ А, так как у ∈ Г(А); разрез пересекали все ребра из А и у, а теперь ситуация изменилась, поэтому общая пропускная способность разреза не может возрасти. (Обратите внимание: нам не нужно беспокоиться об узлах x ∈ X, не входящих в А. Два конца ребра (x, у) будут находиться на разных сторонах разреза, но само ребро не увеличивает пропускную способность разреза, потому что проходит из B' в А'.)
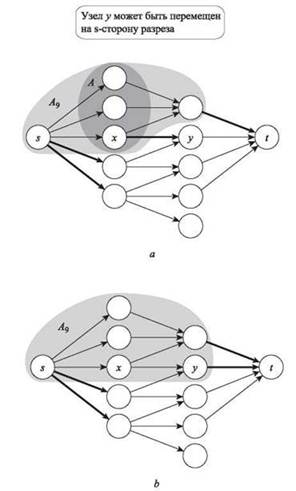
Рис. 7.11. a — минимальный разрез из доказательства (7.40); b — тот же разрез после перемещения узла у на сторону A'. Ребра, пересекающие разрез, выделены жирными линиями
Теперь рассмотрим пропускную способность минимального разреза (A', B'), у которого Г(А) ⊆ A' (рис. 7.11, b). Так как все соседи A принадлежат A', мы видим, что из A' выходят только ребра, либо выходящие из источника s, либо входящие в сток t. Следовательно, пропускная способность разреза равна в точности
![]()
Однако ![]() Из предположения о том, что c(A', B') < n, следует, что
Из предположения о том, что c(A', B') < n, следует, что
![]()
Сравнивая первую и последнюю части, получаем требуемое неравенство |A| > |Г(А)|.