Алгоритмы - Разработка и применение - 2016 год
Выбор проекта - Нахождение потока в сети
Большим (и малым) компаниям постоянно приходится искать баланс между проектами, которые могут принести прибыль, и расходами, необходимыми для обеспечения этих проектов. Предположим, телекоммуникационный гигант CluNet анализирует плюсы и минусы проекта по обеспечению новой услуги высокоскоростного доступа к Интернету для рядовых потребителей. Маркетинговые исследования показывают, что новая услуга принесет неплохой доход, но ее запуск потребует немалых подготовительных затрат: наращивания пропускной способности оптоволоконного кабеля и приобретения скоростных маршрутизаторов последнего поколения.
Подобные решения особенно сложны из-за неочевидных взаимодействий между ними: возможно, сам по себе доход от новой услуги не компенсирует затрат на обновление маршрутизаторов; но с обновленными маршрутизаторами компания сможет предложить выгодный новый проект своим корпоративным клиентам, и этот дополнительный проект изменит баланс. Все эти взаимодействия вызывают цепную реакцию: корпоративный проект в действительности потребует новых расходов, но в свою очередь откроет путь к двум другим выгодным проектам — и т. д. В конечном итоге вопрос звучит так: какими проектами стоит заниматься, а от каких лучше отказаться? Это классическая задача сопоставления затрат с потенциальной выгодой.
Задача
Ниже описана предельно общая структура для моделирования подобных решений. Имеется множество P проектов, с каждым проектом i ∈ P связывается доход рi, который может быть как положительным, так и отрицательным. (Другими словами, каждая выгодная возможность и каждый дорогостоящий шаг по наращиванию инфраструктуры в приведенном выше примере будет рассматриваться как отдельный проект.) Реализация некоторых проектов является предусловием для других проектов; это обстоятельство моделируется направленным ациклическим графом G= (P, E). Узлы G соответствуют проектам, а ребро (i, j) означает, что проект i может быть выбран только в том случае, если также будет выбран проект j. Учтите, что проект i может иметь несколько предусловий, и может быть много проектов, в предусловия которых входит j. Множество проектов A ⊆ P называется действительным, если предусловие каждого проекта в A также принадлежит A: для каждого i ∈ A и каждого ребра (i, j) ∈ E также j ∈ A. Требования, представленные в этой форме, будут называться ограничениями очередности. Прибыль от множества проектов определяется по формуле
![]()
Задача выбора проектов заключается в выборе действительного множества проектов с максимальной прибылью.
В начале 1960-х годов эта задача стала активно изучаться в литературе по анализу данных, где она получила название задачи открытой добычи. “Открытой добычей” называется способ добычи полезных ископаемых, при котором с поверхности берутся земляные блоки для извлечения содержащейся в них руды. Перед началом добычи вся площадь делится на множество Pблоков, и производится оценка чистой стоимости pt каждого блока (то есть цены руды за вычетом затрат на обработку для этого конкретного блока). Одни значения будут положительными, другие отрицательными. В полном множестве блоков действуют ограничения очередности, с которыми некоторые блоки могут извлекаться только после извлечения других блоков, находящихся над ними. Задача открытой добычи формулируется как определение самого выгодного множества извлекаемых блоков с учетом ограничений очередности. Эта формулировка задачи укладывается в структуру выбора проектов — каждый блок соответствует отдельному проекту.
Разработка алгоритма
Сейчас мы покажем, что задача выбора проектов решается посредством сведения к вычислению минимального разреза в расширенном графе G', который определяется по аналогии с графом, использовавшимся в разделе 7.10 для сегментации изображений. Идея заключается в построении G' на базе G таким образом, чтобы сторона источника у минимального разреза в G' соответствовала оптимальному множеству выбираемых проектов.
Чтобы построить граф G', мы добавим в граф G новый источник s и новый сток t, как показано на рис. 7.20. Для каждого узла i ∈ P с рi > 0 добавляется ребро (s, i) c пропускной способностью рi. Для каждого узла i ∈ P c рi < 0 добавляется ребро (i, t) с пропускной способностью –рi. Значения пропускных способностей ребер G мы зададим позднее. Однако уже сейчас видно, что пропускная способность разреза ({s}, P U {t}) равна ![]() поэтому величина максимального потока в этой сети не превышает C.
поэтому величина максимального потока в этой сети не превышает C.
Далее нужно гарантировать, что если (A', B') — минимальный разрез в этом графе, то A = A' - {s} подчиняется ограничениям очередности; то есть если у узла i ∈ A имеется ребро (i, j) ∈ E, то должно выполняться условие j ∈ A. Пожалуй, самым концептуально “чистым” способом будет назначение ребрам G пропускной способности ∞. Ранее понятие бесконечной пропускной способности не формализовалось, но сделать это нетрудно: оно означает лишь то, что такое ребро вообще не имеет верхней границы. Алгоритмы предшествующих разделов, а также теорема о максимальном потоке и минимальном разрезе переносятся для случая бесконечной емкости. Впрочем, введения понятия бесконечной емкости также можно избежать, присвоив каждому из этих ребер “фактически бесконечную” пропускную способность. В нашем контексте для этого достаточно назначить каждому такому ребру пропускную способность C + 1: величина максимального потока в G' не превышает C, поэтому никакой минимальный разрез не может содержать ребро, пропускная способность которого превышает C. Следующее описание работает при любом из этих двух вариантов.
Теперь можно изложить алгоритм: мы вычисляем минимальный разрез (A', B') в G' и объявляем A' - {s} оптимальным множеством проектов. Переходим к доказательству того, что этот алгоритм действительно предоставляет оптимальное решение.
Анализ алгоритма
Начнем с рассмотрения множества проектов A, удовлетворяющего ограничениям очередности. Пусть A' = A U {s} и B' = (P - A) U {t}; рассмотрим разрез s-t (A', B'). Если множество Aудовлетворяет ограничениям очередности, то ни одно ребро (i, j) ∈ E не пересекает этот разрез (рис. 7.20). Пропускная способность разреза выражается следующим образом:
(7.56) Пропускная способность разреза (A', B'), определяемая для множества проектов A с учетом ограничений очередности, равна
![]()
Доказательство. Ребра G' можно разделить на три категории: соответствующие множеству ребер E графа G, выходящие из источника s и входящие в сток t. Так как A удовлетворяет ограничениям очередности, ребра E не пересекают разрез (A', B'), а следовательно, не влияют на его пропускную способность. Ребра, входящие в сток t, вносят в пропускную способность разреза вклад
![]()
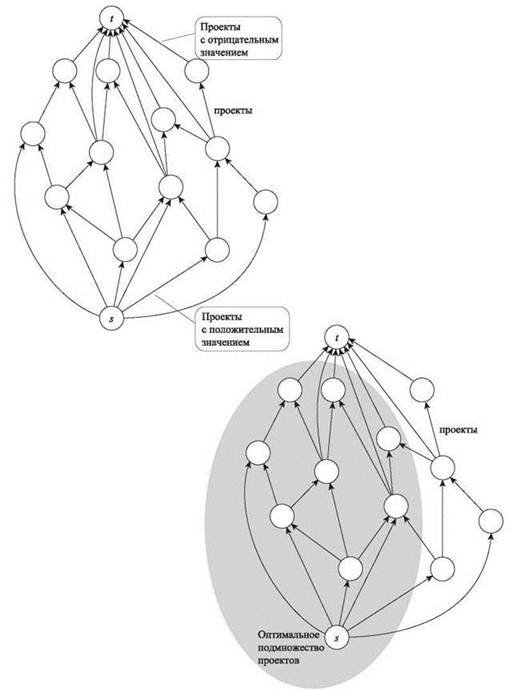
Рис. 7.20. Потоковый граф, используемый для решения задачи выбора проектов. Справа изображен возможный разрез с минимальной пропускной способностью
Вклад ребер, выходящих из источника s, равен
![]()
По определению С последнюю величину можно переписать в виде ![]() Пропускная способность разреза (А', В') равна сумме этих двух слагаемых, то есть
Пропускная способность разреза (А', В') равна сумме этих двух слагаемых, то есть
![]()
как и утверждалось в постановке задачи. ■
Вспомните, что пропускная способность ребер G превышает ![]() а следовательно, такие ребра не могут пересекать разрез, пропускная способность которого не превышает C. Из этого следует, что такие разрезы определяют действительные множества проектов.
а следовательно, такие ребра не могут пересекать разрез, пропускная способность которого не превышает C. Из этого следует, что такие разрезы определяют действительные множества проектов.
(7.57) Если (А', В') — разрез с пропускной способностью, не превышающей С, то множество А = А' - {s} удовлетворяет ограничениям очередности.
Теперь мы можем доказать главную цель всего построения — что минимальный разрез в G' определяет оптимальное множество проектов. Объединяя эти два утверждения, мы видим, что разрезы (A', B'), пропускная способность которых не превышает C, однозначно соответствуют действительным множествам проектов A = A' - {s}. Пропускная способность такого разреза (A', B') составляет
c(A', B') = C – profit(A).
Величина пропускной способности C является константой, не зависящей от разреза (A', B'), поэтому разрез с минимальной пропускной способностью соответствует множествам проектов A с максимальной выгодой profit. Следовательно, нам удалось доказать следующее утверждение.
(7.58) Если (A', B') представляет собой минимальный разрез в G', то множество A = A' - {s} является оптимальным решением задачи выбора проектов.