Выбывание в бейсболе - Нахождение потока в сети

Продюсер в комментаторской говорит: “Видели на той неделе в газете про Эйнштейна?... Один репортер попросил его рассчитать результаты “гонки за флагом”. Знаете, одна команда выигрывает столько-то из оставшихся игр, остальные команды выигрывают столько или столько. Какие возможны варианты? У кого преимущество?

“А он в этом разбирается?”

“Похоже, не очень. Он решил, что “Доджерс” выиграют у “Гигантов” в пятницу””. — Дон Делилло, “Изнанка мира”

Задача

Допустим, вы — репортер из “Алгоритмических спортивных новостей”, и к концу сезона возникает следующая ситуация. Четыре бейсбольные команды пытаются занять первое место в Восточной подгруппе Американской лиги; назовем их “Нью- Йорк”, “Балтимор”, “Торонто” и “Бостон”. На данный момент команды имеют следующее количество побед:

Нью-Йорк: 92, Балтимор: 91, Торонто: 91, Бостон: 90.

В сезоне осталось пять игр: все возможные пары из перечисленных команд, кроме Нью-Йорка и Бостона.

Вопрос заключается в следующем: сможет ли Бостон набрать побед не меньше, чем любая другая команда в подгруппе (то есть закончить на первом месте — возможно, разделив его с другой командой?)

Если немного подумать, становится очевидно, что ответ будет отрицательным. Один из аргументов выглядит так: очевидно, Бостон должен выиграть все оставшиеся игры, а Нью-Йорк должен проиграть обе оставшиеся игры. Но это означает, что и Балтимор, и Торонто выиграют у Нью-Йорка; следовательно, победитель игры Балтимор-Торонто будет иметь больше побед.

Следующий аргумент позволяет избежать подобного анализа. Бостон может набрать не более 92 побед. Совместно три другие команды имеют 274 победы, и в трех играх друг с другом будет ровно три победы, так что итоговая сумма составит 277. Но 277 побед для трех команд означают, что одна из них будет иметь более 92 победы.

Естественно задать некоторые вопросы: (i) Существует ли эффективный алгоритм для определения того, лишилась ли команда шансов на первое место? (ii) Когда команда лишается шансов на первое место, существует ли “усредняющий” алгоритм наподобие описанного выше, который доказывает это?

Перейдем к более конкретной формулировке: имеется множество S команд, для каждой команды х ∈ S текущее количество побед равно wx. Кроме того, две команды x, y ∈ S еще должны сыграть g_xy партий друг с другом. Наконец, задана конкретная команда z.

Мы воспользуемся методами максимального потока для двух целей. Во-первых, будет представлен эффективный алгоритм для принятия решения о том, выбыла ли команда z из соревнования за первое место — другими словами, возможно ли выбрать результаты остальных игр так, чтобы команда z имела побед не меньше, чем любая другая команда в S. Во-вторых, будет доказана теорема об однозначной характеристике выбывания (то есть что всегда можно привести короткое “доказательство” того, что команда потеряла шансы на первое место).

(7.59) Допустим, команда z действительно выбыла из борьбы за первое место. Тогда существует “доказательство” этого факта в следующей форме:

♦ z может закончить игры с максимум m победами.

♦ Существует подмножество команд T ⊆ S, для которого

(А следовательно, одна из команд Tнеизбежно получит строго больше m побед.)

Следующий пример дает более сложную иллюстрацию того, как работает “усредняющий” аргумент (7.59). Предположим, остались те же четыре команды, но с другими количествами текущих побед:

Нью-Йорк: 90, Балтимор: 88, Торонто: 87, Бостон: 79.

У Бостона еще остаются четыре игры против каждой из трех остальных команд. У Балтимора остается еще по одной игре против Нью-Йорка и Торонто. И наконец, Нью-Йорку и Торонто осталось сыграть еще шесть игр друг с другом. Понятно, что для Бостона ситуация выглядит мрачно, но действительно ли он выбыл из борьбы за первое место?

Да, у Бостона действительно не осталось шансов на первое место. Чтобы убедиться в этом, заметьте, что у Бостона может быть не более 91 победы; а теперь рассмотрим множество команд T = {Нью-Йорк, Торонто}. Нью-Йорк и Торонто вместе уже имеют 177 побед; в шести оставшихся играх общее количество побед достигнет 183, а 183/2 > 91. Это означает, что у одной команды неизбежно будет более 91 победы, поэтому Бостон не сможет занять первое место. Любопытно, что в данном экземпляре задачи для множества всех трех команд, опережающих Бостон, такое доказательство не подходит: все три команды имеют в сумме 265 побед, и между ними осталось еще 8 игр; в сумме получается 273, а 273/3 = 91 — этого недостаточно, чтобы доказать, что Бостон не сможет разделить первое место с другими командами. Следовательно, для усредняющего аргумента должно быть выбрано множество T, которое состоит из Нью-Йорка и Торонто и не включает Балтимор.

Разработка и анализ алгоритма

Начнем с построения потоковой сети, предоставляющей эффективный алгоритм для проверки факта выбывания команды z. Затем, анализируя минимальный разрез в сети, мы докажем (7.59).

Очевидно, если для команды z существует вариант, приводящий ее к первому месту, следует рассмотреть вариант, в котором z выигрывает все оставшиеся игры. Допустим, при этом команда выходит с m победами. Теперь нужно тщательно распределить победы во всех остальных играх, чтобы ни одна команда не набрала более m побед. Такое распределение может быть получено посредством вычисления максимального потока на базе следующей идеи: имеется источник s, который генерирует все победы. Победа i может пройти через одну из двух команд, участвующих в i-й игре. Затем устанавливается ограничение пропускной способности, которое говорит, что через команду х могут проходить не более m - w_x.

Конкретнее строится потоковая сеть G, изображенная на рис. 7.21. Пусть S' = S – {z} и — oобщее количество игр, оставшихся между всеми парами команд в S'. В сеть включаются узлы s и t, узел v_x для каждой команды х ∈ S', и узел и для каждой пары команд x, y ∈ S' с ненулевым количеством игр, которые им осталось сыграть друг с другом. Ребра делятся на следующие категории:

♦ ребра (s, u_xy) (победы выходят из s);

♦ ребра (u_xy, v_x) и (u_xy, v_y) (только x или у может победить в игре, в которой они играют друг с другом);

♦ ребра (v_x, t) (победы поглощаются в t).

Какие же пропускные способности следует назначить этим ребрам? От s к u_xy должны передаваться g_xy побед с насыщением, поэтому ребру (s, u_xy) назначается пропускная способность g_xy. Команда x не должна выиграть более m-w_x игр, поэтому ребру (v_x, t) назначается пропускная способность m-w_x. Наконец, ребро в форме (u, v_y) должно иметь как минимум g_xy единиц пропускной способности, чтобы оно могло передать все победы от u_y к v_x; на самом деле самое “чистое” решение — назначить ребру бесконечную пропускную способность. (Построение будет работать даже в том случае, если ребру назначить только g_xy единиц пропускной способности, но доказательство (7.59) при этом усложнится.)

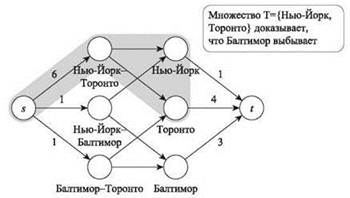
Рис. 7.21. Множество Т={Нью-Йорк, Торонто} доказывает, что Балтимор выбывает

Если существует поток с величиной g*, то результаты всех оставшихся игр могут создать ситуацию, при которой ни одна команда не имеет более m побед; а следовательно, если команда zвыиграет все свои оставшиеся игры, она все равно может добиться хотя бы ничьей за первое место. И наоборот, если для оставшихся игр существуют результаты, с которыми z получает по крайней мере ничью, эти результаты могут использоваться для определения потока с величиной g*. Например, на рис. 7.21, основанном на втором примере, обозначенный разрез показывает, что максимальный поток имеет величину не более 7, тогда как g* = 6 + 1 + 1 = 8.

Итак, мы показали следующий результат:

(7.60) Команда z выбывает из борьбы за первое место в том и только в том случае, если величина максимального потока в G строго меньше g*. Следовательно, проверка выбывания z может быть выполнена за полиномиальное время.

Характеристика выбывания команды

Представленная схема построения сетевого потока также может использоваться для доказательства (7.59). Идея заключается в том, что теорема о максимальном потоке и минимальном разрезе дает удобную характеристику вида “в том и только в том случае” для существования потока; интерпретируя эту характеристику в контексте приложения, мы получим столь же удобную характеристику. Тем самым демонстрируется общий подход к построению теорем характеризации для задач, сводимых к потоку в сети.

Доказательство (7.59). Предположим, команда z выбыла из борьбы за первое место. В этом случае максимальный поток s-t в G имеет величину g' < g*; следовательно, существует разрез s-t (A, B) с пропускной способностью g', и (A, B) является минимальным разрезом. Пусть T — множество команд х, для которых v_x ∈ A. Теперь докажем, что T может использоваться как “усредняющий аргумент” в (7.59).

Сначала рассмотрим узел u_xy и предположим, что х или у не входит в T, но u_xy ∈ A. Тогда ребро (u_xy, v_x) переходит из A в B, а следовательно, разрез (A, B) обладает бесконечной пропускной способностью. Это противоречит предположению о том, что (A, B) является минимальным разрезом с пропускной способностью менее g*. Итак, если одна из команд х или у не входит в T, то u_xy∈ B. С другой стороны, предположим, что х и у принадлежат T, но u_xy ∈ B. Рассмотрим разрез (A', B'), который был бы получен добавлением u_xy в множество A и удалением его из множества B. Пропускная способность (A', B') просто равна пропускной способности (A, B) за вычетом пропускной способности g_xу ребра (s, u_xy) — потому что ребро (s, u_xy) прежде переходило от A к B, а теперь не переходит от A' к B'. Но так как g_ху > 0, это означает, (A', B') обладает меньшей пропускной способностью, чем (A, B), что снова противоречит предположению о минимальности разреза (A, B). Итак, если х и у принадлежат T, то обе команды u_xy ∈ A.

Таким образом, мы пришли к следующему заключению на основании того факта, что (A, B) является минимальным разрезом: u_xу ∈ A в том и только в том случае, если обе команды х, у ∈ T.

А теперь остается лишь найти пропускную способность минимального разреза c(A, B) в контексте пропускных способностей составляющих ребер. Из вывода предыдущего абзаца мы знаем, что ребра, переходящие из A в B, должны иметь одну из следующих двух форм:

♦ ребра в форме (v_x, t), где х ∈ T, и

♦ ребра в форме (s, u_xy), где по крайней мере один из узлов х или у не принадлежит T (другими словами, {х, у} ∉ T).

Следовательно, имеем

Так как мы знаем, что c(A, B) = g' < g* из последнего неравенства вытекает

а следовательно,

Например, применяя аргумент из доказательства (7.59) к экземпляру на рис. 7.21, мы видим, что узлы Нью-Йорка и Торонто расположены на стороне источника относительно минимального разреза, и как было показано ранее, эти две команды действительно доказывают, что Бостон выбыл из борьбы за первое место.