Классификация на базе локального поиска - Локальный поиск

В этом разделе рассматривается более сложный пример применения локального поиска при разработке аппроксимирующих алгоритмов, связанный с задачей о сегментации изображения, которая рассматривалась среди практических применений сетевых потоков в разделе 7.10. Более сложная версия сегментации изображения, которая будет рассматриваться здесь, дает пример того, как для получения хорошего быстродействия алгоритма локального поиска приходится использовать довольно сложную структуру соседского окружения для множества решений. Как вы увидите, естественное соседское окружение “переключения состояния”, описанное в предыдущем разделе, может приводить к очень плохим локальным оптимумам. Для получения хорошего быстродействия мы воспользуемся экспоненциально большим соседским окружением. Одна из проблем больших соседских окружений заключается в том, что последовательный поиск по всем соседям текущего решения для его улучшения становится неприемлемым. Потребуется более сложный алгоритм поиска улучшенного соседа (если он существует).

Задача

Вспомним базовую задачу сегментации изображения, приведенную как пример использования потоков в разделе 7.10. Тогда задача сегментации изображения была сформулирована как задача разметки; наша цель заключалась в пометке (то есть классификации) каждого пиксела как принадлежащего к переднему плану или фону изображения. На тот момент было понятно, что это очень простая формулировка задачи и было бы неплохо иметь заняться более сложными задачами разметки, например сегментацией областей изображения в зависимости от их расстояния от камеры. По этой причине мы рассмотрим задачу разметки с более чем двумя метками. Попутно мы создадим инфраструктуру классификации, возможности применения которой не ограничиваются пикселами изображения.

При определении задачи сегментации с двумя метками “передний план/фон” мы в конечном итоге пришли к следующей формулировке. Имеется граф G = (V, E), в котором V соответствует пикселам изображения, а цель заключается в классификации каждого узла V по двум возможным классам: фону и переднему плану. Ребра представляют пары узлов, которые с большой вероятностью принадлежат одному классу (например, потому что они расположены вблизи друг от друга), и для каждого ребра (i, j) задан штраф р_ij ≥ 0 за размещение i и j в разных классах. Кроме того, имеется информация о вероятности того, принадлежит узел или пиксел переднему плану или фону. Эти вероятности были преобразованы в штрафы за отнесение узла к классу, которому он принадлежит с меньшей вероятностью. Задача заключалась в нахождении разметки узлов, минимизировавшей общие штрафы за разделение и отнесение к классу. Мы показали, что задача минимизации решается посредством вычисления минимального разреза. В оставшейся части раздела эта формулировка задачи будет называться бинарной сегментацией изображения.

Сейчас будет сформулирована аналогичная задача классификации/разметки с более чем двумя классами (метками). Как выясняется, эта задача является NP-сложной, и мы разработаем алгоритм локального поиска, в котором локальные оптимумы являются 2-аппроксимациями для лучшей разметки. Обобщенная задача разметки, рассматриваемая в этом разделе, формулируется следующим образом. Имеются граф G = (V, E) и множество L из k меток. Целью является пометка каждого узла в V одной из меток из множества L с целью минимизации некоторого штрафа. На выбор оптимальной разметки влияют два конкурирующих фактора. Для каждого ребра (i, j) ∈ E действует штраф за разделение р_ij ≥ 0 за пометку двух узлов i и jразными метками. Кроме того, узлы с большей вероятностью имеют одни метки вместо других. Это условие выражается штрафом за назначение. Для каждого узла i ∈ V и каждой метки a ∈ Lдействует неотрицательный штраф c_i(a) ≥ 0 за назначение метки а узлу i. (Эти штрафы являются аналогами вероятностей из задачи бинарной сегментации, не считая того, что здесь они рассматриваются как минимизируемые затраты.) Задача разметки заключается в нахождении разметки f: V → L, минимизирующей общий штраф:

Заметим, что задача разметки только с двумя метками в точности совпадает с задачей сегментации изображений из раздела 7.10. Для трех меток задача разметки уже является NР-сложной, хотя этот факт мы доказывать не будем.

Наша цель — разработать алгоритм локального поиска для этой задачи, в котором локальные оптимумы являются хорошими аппроксимациями оптимального решения. Пример также наглядно покажет, как важно выбирать хорошее соседское окружение для определения алгоритма локального поиска. Существует много возможных вариантов для соседских отношений, и вы увидите, что некоторые из них работают намного лучше других. В частности, для получения гарантий аппроксимации будет использовано довольно сложное определение соседского окружения.

Разработка алгоритма

Первая попытка: правило одного переключения

Простейшим и, наверное, самым естественным выбором соседского отношения является правило одного переключения из алгоритма переключения состояния для задачи о максимальном разрезе: две разметки являются соседними, если одну из них можно получить из другой изменением метки одного узла. К сожалению, это соседство может привести к достаточно слабым локальным оптимумам в нашей задаче, даже всего с двумя метками.

Это выглядит несколько странно, потому что правило хорошо работало в задаче о максимальном разрезе. Однако наша задача связана с задачей о минимальном разрезе. Собственно, задача о минимальном разрезе s-t соответствует частному случаю, в котором используются всего две метки, а s и t — единственные узлы со штрафами назначения. Нетрудно увидеть, что этот алгоритм переключения состояния не является хорошим аппроксимирующим алгоритмом для задачи о минимальном разрезе. Из рис. 12.5 видно, как ребра, инцидентные s, могут образовать глобальный оптимум, тогда как ребра, инцидентные t, могут образовать намного худший локальный оптимум.

Вторая попытка: рассмотрение двух меток за раз

Здесь мы разработаем алгоритм локального поиска, в котором окружение определяется намного сложнее. Интересная особенность этого алгоритма заключается в том, что он позволяет каждому решению иметь экспоненциальное количество соседей. На первый взгляд это противоречит общему правилу “соседское окружение решения не должно быть слишком большим”, как утверждалось в разделе 12.5. Однако здесь мы будем работать с окружением более элегантно. Сохранение малого размера соседского окружения хорошо работает тогда, когда вы планируете проводить поиск улучшающего локального шага методом “грубой силы”; а на этот раз мы воспользуемся вычислением минимального разреза с полиномиальным временем, чтобы определить, встречается ли улучшение среди экспоненциально многочисленных соседей решения.

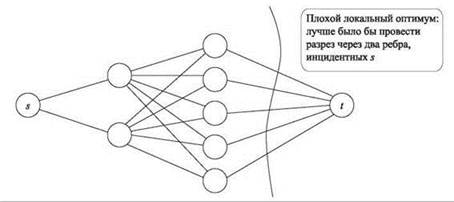
Рис. 12.5. Экземпляр задачи о минимальном разрезе s-t, в котором пропускные способности всех ребер равны 1

Идея локального поиска заключается в применении алгоритма с полиномиальным временем для бинарной сегментации изображения с целью улучшения локальных шагов. Начнем с простейшей реализации этой идеи, которая не всегда дает хорошую гарантию аппроксимации. Для разметки f выберем две метки a, b ∈ L и ограничим внимание узлами, имеющими метки а или b в разметке f. За один локальный шаг любое подмножество этих узлов может переключить метки из а в b или из b в а. Или в более формальном определении, две разметки f и f' считаются соседними, если существуют две метки a, b ∈ L, такие, что для всех остальных меток c ∉ {a, b} и всех узлов i ∈ V условие f(i) = c выполняется в том, и только в том случае, если f'(i) = c. Следует заметить, что состояние f может иметь сколь угодно много соседей, так как произвольное подмножество узлов с метками a и b может переключать свою метку. Однако при этом действует следующее утверждение:

(12.8) Если разметка f не является локально оптимальной для описанного выше соседского окружения, то сосед с меньшим штрафом может быть найден за k² вычислений минимального разреза.

Доказательство. Количество пар разных меток меньше k², поэтому каждую пару можно проверить по отдельности. Для пары меток a, b ∈ L рассмотрим задачу нахождения улучшенной разметки посредством перестановки меток узлов между а и b. Она в точности совпадает с задачей сегментации для двух меток в подграфе узлов, которым в f назначены метки а или b. Воспользуемся алгоритмом, разработанным для бинарной сегментации изображений, для поиска лучшей из таких измененных разметок. ■

Это соседское окружение намного лучше варианта с одним переключением, который был рассмотрен в начале. Например, оно предоставляет оптимальное решение случая с двумя метками. Однако даже с улучшенным окружением локальные оптимумы могут быть плохими, как показано на рис. 12.6. В этом примере есть три узла s, t и z, которые должны сохранить свои исходные метки. Все остальные узлы лежат на одной из сторон треугольника; они должны сохранить одну из двух меток, связанных с узлами на концах этой стороны. Эти требования легко выражаются назначением каждому узлу очень большого штрафа за назначение для неразрешенных меток. Штрафы за разделение определяются следующим образом: тонким ребрам на рисунке соответствует штраф 1, а толстым — большой штраф M. Теперь заметим, что разметка на иллюстрации имеет штраф M + 3, но при этом является локально оптимальной. У (глобально) оптимальной разметки штраф равен всего 3, а для ее получения на рисунке достаточно изменить метки обоих узлов рядом с s.

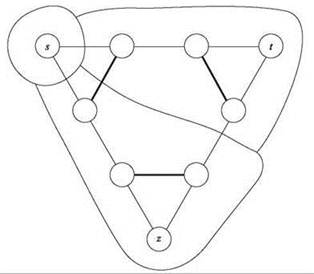
Рис. 12.6. Плохой локальный оптимум для алгоритма локального поиска, учитывающего только две метки

Работоспособное соседское окружение при локальном поиске

Теперь мы определим другое соседское окружение, приводящее к хорошему алгоритму аппроксимации. Локальный оптимум на рис. 12.6 наводит на мысль о том, что могло бы быть хорошим соседским окружением: нужно иметь возможность переназначения меток узлов за один шаг. Для этого необходимо найти соседское отношение, которое было бы достаточно широким для выполнения этого свойства, но при этом позволяло найти улучшающий локальный шаг за полиномиальное время.

Рассмотрим разметку f. В процессе локального шага нашего нового алгоритма должно происходить следующее: мы выбираем одну метку а ∈ L и ограничиваем рассмотрение узлами, не имеющими метки а в разметке f. За один локальный шаг любому подмножеству этих узлов разрешается изменить свои метки на а. Или в более формальном определении, две разметки f и f' считаются соседними, если существует метка а ∈ L, такое что для всех узлов i ∈ V либо f'(i) = f(i), либо f'(i) = а. Обратите внимание на то, что это соседское отношение не является симметричным; другими словами, f не удастся получить обратно из f' за один шаг. Теперь мы покажем, что для любой разметки f любого соседа можно найти за k вычислений минимального разреза, а локальный оптимум этого соседского окружения является 2-аппроксимацией разметки с минимальным штрафом.

Поиск хорошего соседа

Чтобы найти лучшего соседа, мы проверяем каждую метку по отдельности. Начнем с метки а. Утверждается, что лучшее переназначение, в котором узлы могут изменить свои метки на а, может быть найдено посредством вычисления минимального разреза. Построение графа минимального разреза G' = (V', E') аналогично вычислению минимального разреза, разработанному для бинарной сегментации изображений. Тогда мы определили источник s и сток t для представления двух меток. Здесь мы тоже введем источник и сток, но источник s будет представлять метку а, а сток t будет фактически представлять другой вариант, имеющийся у узлов, а именно сохранение их исходных меток. Идея заключается в том, чтобы найти минимальный разрез в G' и заменить метки всех узлов на стороне s разреза меткой а, тогда как все узлы на стороне t сохранят свои исходные метки.

Для каждого узла G в новом множестве V' имеется соответствующий узел, а в E' добавляются ребра (i, t) и (s, i), как это делалось на рис. 7.18 из главы 7 в случае двух меток. Ребро (i, t) имеет пропускную способность с_i(а), так как разрезание ребра (i, t) приводит к размещению узла i на стороне источника, а следовательно, соответствует пометке узла i меткой а. Ребро (i, s) будет иметь пропускную способность c_i(f(i)), если f(i) ≠ а, или она будет выражаться очень большим числом M (или +∞), если f(i) = а. Разрезание ребра (i, t) помещает узел i на сторону стока, а следовательно, соответствует сохранению узлом i исходной метки f(i) ≠ а. Большая пропускная способность M предотвращает размещение узлов i с f(i) = а на стороне стока.

В построении для задачи с двумя метками мы добавляли ребра между узлами V и использовали штрафы за разделение как пропускные способности. Этот способ хорошо работает для узлов, разделенных разрезом, или узлов на стороне источника, одновременно имеющих метку а. Но если i и j находятся на стороне стока, то соединяющее их ребро еще не разрезано, но i и jразделены, если f(i) ≠ f(j). Чтобы решить эту проблему, мы дополним построение G' следующим образом. Для ребра (i, j), если f(i) = f(j) или один из узлов i илиj имеет метку а, в E' добавляется ребро (i, j) с пропускной способностью p_ij. Для ребер е = (i, j), у которых f(i) ≠ f(j) и ни один узел не имеет метку а, чтобы правильно закодировать через граф G', что i и j остаются разделенными, даже если находятся на стороне стока, придется действовать иначе. Для каждого такого ребра e в V' добавляется дополнительный узел е, соответствующий ребру е, и ребра (i, е), (е, j) и (е, s) с пропускной способностью p_ij. Эти ребра изображены на рис. 12.7.

Рис. 12.7. Построение для ребра е = (i, j) с а ≠ f(i) ≠ f(j) ≠ а

(12.9) Для заданной разметки f и метки а минимальный разрез в графе G' = (V, E') соответствует соседу разметки f с минимальным штрафом, полученному заменой меток подмножества узлов на а. В результате сосед f с минимальным штрафом может быть найден посредством k вычислений минимального разреза, по одному для каждой метки в L.

Доказательство. Пусть (A, B) — разрез s-t в G'. Большое значениеMгарантирует, что разрез с минимальной пропускной способностью не разрежет никакие из этих ребер с высокой пропускной способностью. Теперь рассмотрим узел е в G', соответствующий ребру е = (i, j) ∈ E. Узел е ∈ V' имеет три прилегающих ребра, каждое из которых имеет пропускную способность p_ij. Для любого разбиения остальных узлов е можно разместить так, что разрезано будет не более одного из этих трех ребер. Назовем разрез хорошим, если никакое ребро с пропускной способностьюM не разрезается и для всех узлов, соответствующих ребрам в E, разрезается не более одного из прилегающих ребер. К настоящему моменту мы обосновали, что все разрезы с минимальной пропускной способностью являются хорошими.

Хорошие разрезы s-t в G' находятся в однозначном соответствии с переназначениями меток f, полученными заменой метки подмножества узлов на а. Рассмотрим пропускную способность хорошего разреза. Ребра (s, i) и (i, t) добавляют в пропускную способность разреза в точности штраф за назначение. Ребра (i, j), напрямую соединяющие узлы в V, вносят в точности штраф за разделение узлов в соответствующей разметке: р_ij, если они разделены, и 0 в противном случае. Наконец, рассмотрим ребро е = (i, j) с соответствующим узлом е ∈ V'. Если оба узла i и jнаходятся на стороне источника, ни одно из трех ребер, прилегающих к е, не будет разрезано, а во всех остальных случаях разрезается ровно одно из этих ребер. Итак, три ребра, прилегающие к е, добавляют к разрезу в точности величину штрафа за разделение между i и j в соответствующей разметке. В результате пропускная способность хорошего разреза в точности совпадает со штрафом соответствующей разметки, а следовательно, разрез с минимальной пропускной способностью соответствует лучшему переназначению меток f. ■

Анализ алгоритма

Наконец, необходимо рассмотреть качество локальных оптимумов при таком определении соседских отношений. Вспомните, что в двух предыдущих попытках определения соседского окружения выяснилось, что в обоих случаях мы приходим к плохим локальным оптимумам. Теперь мы покажем, что любой локальный оптимум с новым соседским отношением является 2-аппроксимацией минимального возможного штрафа.

Начнем с рассмотрения оптимальной разметки f*; пусть для метки a ∈ L V*_a = {i: f*(i) = a} обозначает множество узлов с меткой а в f*. Рассмотрим локально оптимальную разметку f. Чтобы получить соседа f_a разметки f, мы заменим метки всех узлов в V*_а на а. Разметка f является локально оптимальной, а следовательно, этот сосед f_a имеет не меньший штраф: Ф(f_a) ≥ Ф(f). Рассмотрим разность Ф(f_a) - Ф(f), которая, как мы знаем, не отрицательна. Какие величины вносят свой вклад в эту разность? Единственное возможное изменение в штрафах за назначение может происходить от узлов в V*_a: для каждого i ∈ V*_a изменение равно c_i(f*(i)) - c_i(f(i)). Штрафы за разделение между двумя разметками различаются только в ребрах (i, j), по крайней мере один конец которых находится в V*_a. Следующее неравенство учитывает эти различия.

(12.10) Для разметки f и ее соседа f_a

Доказательство. Изменение в штрафах за назначение равно

Штраф за разделение для ребра (i, j) может различаться между двумя разметками только в том случае, если по крайней мере один конец ребра (i, j) принадлежит V*_d. Общий штраф за разделение в разметке f для таких ребер равен в точности

тогда как в разметке f_a штраф за разделение не превышает

для этих ребер. (Обратите внимание: последнее выражение всего лишь определяет верхнюю границу, так как ребро (i, j), выходящее из V*_d, другой конец которого находится в а, не участвует в штрафе за разделение f_a.) ■

Теперь можно переходить к доказательству основного утверждения.

(12.11) Для любой локально оптимальной разметки f и любой другой разметки f* - Ф(f) ≥ 2Ф(f*).

Доказательство. Пусть f_a — сосед f, определенный ранее переназначением меток узлов на а. Разметка f является локально оптимальной, поэтому имеем Ф(f_а) - Ф(f) ≥ 0 для всех а ∈ L. Используем (12.10) для ограничения Ф(f_а) - Ф(f), а затем просуммируем полученные неравенства для всех меток с получением следующего результата:

Сгруппируем положительные слагаемые в левой части, а отрицательные — в правой. В левой части получаем c_i(f*(i)) для всех узлов i, что в точности равно штрафу за назначение f*. Кроме того, слагаемое p_ij учитывается дважды для каждого из ребер, разделенных f* (по одному разу для каждой из двух меток f*(i) и f*(j)).

В правой части получаем c_i(f(i)) для всех узлов i, что в точности равно штрафу за назначение f. Кроме того, учитываются слагаемые p_ij для ребер, разделенных f. Каждый такой штраф за разделение учитывается хотя бы один раз, а возможно и дважды, если разделение также встречается в f*.

В итоге получаем следующее.

Граница в утверждении доказана. ■

Мы доказали, что все локальные оптимумы являются хорошими аппроксимациями для разметок с минимальным штрафом. Осталось разобраться еще с одним вопросом: насколько быстро алгоритм находит локальный оптимум? Вспомните, что в случае задачи о максимальном разрезе нам пришлось прибегнуть к разновидности алгоритма, которая принимала только большие улучшения, так как повторные локальные улучшения могли не обеспечить полиномиальное время выполнения. То же самое происходит и здесь: пусть є > 0 — константа. Для заданной разметки f мы будем считать соседнюю разметку f' значительным улучшением, если Ф(f') ≤ (1 - є/3k) Ф(f). Чтобы алгоритм выполнялся за полиномиальное время, следует принимать только значительные улучшения и завершать его выполнение, когда они невозможны. После максимум є^-1k значительных улучшений штраф уменьшается с постоянным множителем; следовательно, алгоритм завершится за полиномиальное время. Доказательство (12.11) нетрудно адаптировать для того, чтобы доказать следующее.

(12.12) Для любого фиксированного є > 0 версия алгоритма локального поиска, принимающая только значительные улучшения, завершается за полиномиальное время и приводит к такой разметке f, что Ф(f) ≤ (2 + є) Ф(f*) для любой другой разметки f*.