Динамика наилучших ответов и равновесия Нэша - Локальный поиск

До настоящего момента мы рассматривали локальный поиск как метод решения оптимизационных задач только с единственной целью — другими словами, применяли локальные операции к потенциальному решению для минимизации его общей стоимости. Однако существует много других настроек, в которых решение некоторой задачи строится коллективным взаимодействием большого количества агентов, каждый из которых имеет собственные цели. Решение, полученное в таких обстоятельствах, часто отражает процесс “перетягивания каната”, которое к нему привело, когда каждый агент пытается сместить решение в благоприятном для себя направлении. Вы увидите, что такие взаимодействия могут рассматриваться как разновидность процедуры локального поиска; аналогии локальных минимумов также имеют естественный смысл, но наличие множественных агентов и множественных целей создает новые проблемы.

Область теории игр предоставляет естественную основу для обсуждения того, что происходит в ситуациях стратегического взаимодействия множества агентов, то есть, когда каждый пытается оптимизировать свою целевую функцию. Чтобы продемонстрировать возникающие проблемы, мы рассмотрим практический пример из области сетевой маршрутизации; попутно будут представлены некоторые понятия, играющие важную роль в области более общей теории игр.

Задача

В такой сети, как Интернет, часто встречаются ситуации, в которых сразу несколько узлов пытаются установить связь с одним узлом-источником s. Например, источник s может генерировать некий поток данных, который желают получать все узлы, — по аналогии со схемой сетевых взаимодействий “один ко многим”, называемой многоадресной передачей(multicast). Описанная ситуация моделируется представлением сети в виде направленного графа G = (V, E), со стоимостью с_е ≥ 0 каждого ребра. Имеется выделенный узел-источник s ∈ V и набор из k агентов, расположенных в разных терминальных узлахt₁, t₂, ..., t_k ∈ V. Для простоты мы не будем различать агентов и узлы, в которых они находятся; другими словами, агенты будут рассматриваться как t₁, t₂, ..., t_k.

Каждый агент t_j стремится построить путь P_j из s в t_j с минимальной общей стоимостью. При отсутствии взаимодействий между объектами задача распадается на k отдельных задач о кратчайшем пути: каждый агент t_j находит путь s-t_j, минимизирующий общую стоимость всех ребер, и использует его как свой путь P_j. В этой задаче интересна возможность “совместного использования” стоимости ребер агентами. Допустим, после того, как все агенты выберут свои пути, агенту t_j достаточно заплатить “свою долю” стоимости каждого ребра е на своем пути; иначе говоря, вместо того, чтобы платить с_е для каждого ребра e в P_i, он платит величину c_e, разделенную на количество агентов, пути которых содержат е. Таким образом у агентов появляется стимул для использования перекрывающихся путей, потому что они могут выиграть от разбивки стоимости ребер. (Эта модель подходит для конфигураций, в которых использование ребра несколькими агентами не приводит к значительному снижению качества передачи из-за перегрузки или увеличения задержки. Если эффекты задержки начинают действовать, вводится компенсирующий штраф за совместное использование; эта ситуация также приводит к интересным алгоритмическим вопросам, но мы пока будем придерживаться текущей формулировки, в которой совместное использование приносит только выгоду.)

Динамика наилучших ответов и равновесия Нэша: определения и примеры

Чтобы понять, как возможность совместного использования влияет на поведение агентов, для начала рассмотрим пару очень простых примеров на рис. 12.8. В примере а у каждого из двух агентов есть два варианта построения пути: средний маршрут через v и внешний маршрут с использованием одного ребра. Предположим, каждый агент начинает с исходного пути, но постоянно пересчитывает текущую ситуацию, чтобы решить, возможно ли перейти на лучший путь.

Допустим, в примере а два агента начинают с использования внешних путей. Затем t₁ не видит преимущества в переходе на другой путь (так как 4 < 5 + 1), но у t₂ такое преимущество есть (так как 8 > 5 + 1), поэтому t₂ обновляет свой путь с переходом на середину. Когда это происходит, с точки зрения t₁ ситуация изменяется: внезапно у t₁ также появляется выгода от перехода, так как он сможет оплатить лишь часть стоимости среднего пути, и для него стоимость пути сокращается до 2,5 + 1 < 4. Соответственно t₁ переходит на новый путь. В ситуации, в которой обе стороны используют средний путь, ни у кого нет стимула для перехода, поэтому такое решение может считаться устойчивым.

Рис. 12.8. Совместное использование среднего пути в интересах обоих агентов (а). Для всех агентов было бы лучше использовать левое ребро. Но если все к агентов начнут с правого ребра, ни один из них не захочет в одностороннем порядке перейти справа налево (b); другими словами, решение, в котором все агенты совместно используют ребро справа, является плохим равновесием Нэша

Обсудим два определения из области теории игр, в которых отражено происходящее в этом простом примере. Хотя мы по-прежнему будем ориентироваться на конкретную задачу маршрутизации при многоадресной передаче, эти определения подходят для любых конфигураций с нескольким агентами (каждый из которых обладает своей целью), взаимодействующими для выработки коллективного решения. Соответственно в определениях будут использованы эти общие термины.

♦ Прежде всего, в представленном примере каждый агент был всегда готов улучшить свое решение в ответ на изменения, внесенные другими агентами. Мы будем называть этот процесс динамикой наилучших ответов. Другими словами, нас интересует динамическое поведение процесса, в котором каждый агент обновляет свое состояние в зависимости от своего наилучшего ответа на текущую ситуацию.

♦ Кроме того, нас особенно интересуют устойчивые решения, в которых лучший ответ каждого агента должен оставаться неизменным. Такое решение, в котором ни у одного агента нет стимула для отклонения, называется равновесием Нэша (по имени математика Джона Нэша, получившего Нобелевскую премию по экономике за свою новаторскую работу по этой концепции). Следовательно, в примере а решение, в котором оба агента используют средний путь, является равновесием Нэша. Обратите внимание: равновесия Нэша точно соответствуют решениям, в которых завершается динамика наилучших ответов.

Пример на рис. 12.8, b демонстрирует возможность существования нескольких равновесий Нэша. В этом примере все к агентов находятся в общем узле t (то есть t₁ = t₂ = ... = t_k = t), и из s в tведут два параллельных ребра с разной стоимостью. Решение, в котором все агенты используют левое ребро, представляет собой равновесие Нэша, где каждый агент платит (1 + ε)/k. Решение, в котором все агенты используют правое ребро, также является равновесием Нэша, хотя в этом случае каждый агент платит k/k = 1. Этот факт подчеркивает один важный аспект динамики наилучших ответов: если агенты смогут как-то согласовать одновременный переход с правого ребра на левое, в целом они от этого выиграют. Однако в динамике наилучших ответов каждый агент оценивает только последствия от своего одностороннего перемещения. По сути, агент не может делать никакие предположения относительно будущих действий других агентов (в среде Интернета он может даже ничего не знать о существовании таких агентов или их текущих решениях), поэтому агент желает выполнять только те обновления, которые приводят к немедленному улучшению ситуации для него самого.

Для количественного выражения смысла, в котором одно из равновесий Нэша на рис. 12.8, b лучше другого, полезно ввести еще одно определение. Решение называется социальным оптимумом, если оно минимизирует общую стоимость для всех агентов. Такое решение могло бы быть принято центральным органом, с точки зрения которого все агенты имеют одинаковый приоритет, и поэтому качество общего решения оценивается простым суммированием их затрат. Следует заметить, что в a и b существует социальный оптимум, который также является равновесием Нэша, хотя в b также существует второе равновесие Нэша с много большей стоимостью.

Связь с локальным поиском

К этому моменту постепенно начинает проступать связь с локальным поиском. Множество агентов, следующих динамике наилучших ответов, участвует в своего рода процессе градиентного спуска, исследуя “поверхность” возможных решений в стремлении к минимизации отдельных стоимостей. Равновесия Нэша являются естественными аналогиями локальных минимумов в этом процессе: это решения, для которых невозможны улучшающие перемещения. “Локальная” природа поиска также очевидна, поскольку агенты обновляют свои решения только тогда, когда это приводит к немедленному улучшению.

Впрочем, даже с учетом сказанного стоит отметить ряд критических отличий от стандартного локального поиска. В начале главы мы могли легко обосновать, что алгоритм градиентного спуска для комбинаторной задачи должен завершиться в локальном минимуме: каждое обновление уменьшало стоимость решения, а поскольку количество возможных решений было конечным, серия обновлений не могла продолжаться бесконечно. Другими словами, сама функция стоимости предоставляла метрику прогресса, необходимую для обоснования завершения.

С другой стороны, в динамике наилучших ответов каждый агент имеет собственную целевую функцию, которую он пытается минимизировать, поэтому не так очевидно, какой общий “прогресс” происходит, например, при обновлении агентом t_i своего пути из s. Конечно, для t_i прогресс существует, поскольку его стоимость пути снижается, но снижение может быть скомпенсировано еще большим возрастанием стоимости у другого агента. Для примера рассмотрим сеть на рис. 12.9. Если оба агента начинают со среднего пути, то у t₁ будет стимул для перехода на внешний путь; его стоимость уменьшается с 3,5 до 3, но в процессе стоимость t₂ увеличивается с 3,5 до 6. (Когда это произойдет, t₂ также переместится на внешний путь, и это решение — при котором оба узла используются внешними путями — является уникальным равновесием Нэша.)

Рис. 12.9. Сеть, в которой уникальное равновесие Нэша отличается от социального оптимума

Впрочем, в некоторых ситуациях эффекты возрастания стоимости динамики наилучших ответов могут быть намного худшими. Взгляните на рис. 12.10: имеются k агентов, каждый из которых имеет возможность выбрать общий внешний путь со стоимостью 1 + ε (для некоторого малого числа ε > 0) или собственный альтернативный путь. Альтернативный путь для t_j имеет стоимость 1/j. Теперь предположим, что мы начинаем с решения, в котором все агенты совместно используют внешний путь. Каждый агент платит (1 + ε)/k, и это решение минимизирует общую стоимость по всем агентам. Но с применением динамики наилучших ответов, начиная с этого решения, события начинают стремительно развиваться. Сначала t_k переключается на свой альтернативный путь, так как 1/k < (1 + ε)/k. В результате теперь внешний путь используется только k - 1 агентами, поэтому t_k - 1 переходит на альтернативный путь, так как 1/(k - 1) < (1 + ε)/(k - 1). После этого переходит t_k - 2, потом t_k - 3, и т. д., пока все к агентов не будут использовать альтернативные пути прямо из s. Здесь изменения временно прекращаются из-за следующего факта.

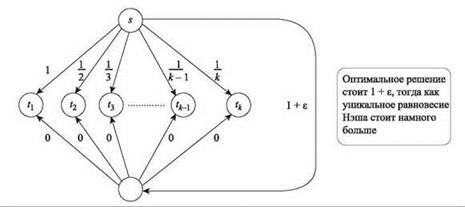
Рис. 12.10. Сеть, в которой уникальное равновесие Нэша стоит в H(k) = Ө(log k) раз больше социального оптимума

(12.13) Решение на рис. 12.10, в котором каждый агент использует свой прямой путь от s, является равновесием Нэша; более того, в данном экземпляре оно является уникальным равновесием Нэша.

Доказательство. Чтобы убедиться в том, что данное решение является равновесием Нэша, достаточно проверить, что ни у одного агента нет причин для перехода с его текущего пути. Но это очевидно, поскольку все агенты платят не более 1, а единственный другой вариант — (в настоящее время свободный) внешний путь — имеет стоимость 1 + ε.

А теперь предположим, что существует другое равновесие Нэша. Чтобы оно отличалось от рассматриваемого решения, в нем должен быть задействован по крайней мере один из агентов, использующих внешний путь. Пусть t_j1, t_j2, ..., t_jl — агенты, использующие внешний путь, где j₁ < j₂ < ... < j_l. Тогда все эти агенты платят (1 + ε)/l. Но обратите внимание на то, что jl ≥ l, и у агента t_jl есть возможность заплатить только 1/jl ≤ 1/l за счет использования альтернативного пути прямо из s. Следовательно, у t_jl есть стимул для отклонения от текущего решения, а значит, решение не может быть равновесием Нэша. ■

Рисунок 12.8, b уже показал, что может существовать равновесие Нэша с общей стоимостью гораздо худшей, чем у социального оптимума, но примеры на рис. 12.9 и 12.10 наглядно раскрывают еще более важный момент: общая стоимость для всех агентов даже в самом выгодном решении с равновесием Нэша может быть хуже общей стоимости в социальном оптимуме. Насколько хуже? Общая стоимость социального оптимума в этом примере равна 1 + ε, тогда как стоимость уникального равновесия Нэша составляет Это выражение уже встречалось в главе 11, где мы определили его как гармоническое числоH(k) и показали, что его асимптотическое значение равно H(k) = Ө(log k).

Эти примеры поясняют, что социальный оптимум не следует рассматривать как аналогию глобального минимума в традиционной процедуре локального поиска. При стандартном локальном поиске глобальный минимум всегда является устойчивым решением, так как никакие улучшения невозможны. Однако социальный оптимум может быть неустойчивым решением, так как для этого достаточно, чтобы всего один агент был заинтересован в отклонении.

Два основных вопроса

Динамика наилучших ответов может проявлять разнообразные варианты поведения, и мы уже видели несколько примеров, демонстрирующих разные аспекты. Будет полезно сделать шаг назад, оценить наш текущий уровень понимания и задать некоторые основные вопросы. Мы объединим их в две группы.

♦ Существование равновесия Нэша. На данный момент мы еще не располагаем доказательствами того, что решение с равновесием Нэша хотя бы существует в каждом экземпляре задачи многоадресной передачи. Самый естественный кандидат на метрику прогресса — общая стоимость всех агентов — не обязательно убывает при обновлении одним агентом его пути.

С учетом этого обстоятельства даже неясно, как обосновать, что динамика наилучших ответов должна завершиться. Почему не может возникнуть цикл, при котором агент t₁ улучшает свое решение за счет t₂, а затем t₂ улучшает свое решение за счет t₁, и т. д. до бесконечности? В самом деле, нетрудно определить другие задачи, в которых возникает именно такая ситуация и в которых равновесия Нэша не существует. Чтобы обосновать, что динамика наилучших ответов ведет к равновесию Нэша в данном случае, необходимо разобраться, что же такого особенного в задаче маршрутизации.

♦ Цена устойчивости. До настоящего момента равновесие Нэша рассматривалось в основном в роли “наблюдателей”: фактически мы “выпускаем” агентов на граф в произвольной начальной точке и смотрим, что они сделают. Но если рассматривать происходящее с точки зрения разработчиков протокола, пытаясь определить процедуру построения агентами путей из s, можно пойти по следующему пути: для заданного множества агентов, находящихся в узлах t₁, t₂, ..., t_k, можно предложить множество путей (по одному для каждого агента), обладающее двумя свойствами:

(i) Множество путей образует решение с равновесием Нэша;

(ii) С учетом (i) общая стоимость для всех агентов настолько мала, насколько это возможно.

Конечно, в идеале нам хотелось бы добиться наименьшей общей стоимости, как при социальном оптимуме. Но если предложить социальный оптимум, который не является равновесием Нэша, он не будет устойчивым: агенты начнут отклоняться и строить новые пути. Таким образом, свойства (i) и (ii) совместно представляют попытку нашего протокола найти оптимум с учетом устойчивости и отыскать лучшее решение, от которого ни один агент не захочет отойти. По этой причине для заданного экземпляра задачи определяется цена устойчивости как отношение стоимости лучшего решения с равновесием Нэша к стоимости социального оптимума. Эта характеристика отражает рост стоимости, обусловленный требованием о том, что наше решение должно быть устойчивым в контексте личного интереса каждого агента.

Эту пару вопросов можно задать практически для любой задачи, в которой агенты с собственными интересами генерируют коллективное решение. Мы сейчас ответим на оба вопроса для задачи маршрутизации при многоадресной передаче. Как выясняется, пример на рис. 12.10 отражает некоторые критические аспекты задачи в целом. Мы покажем, что для любого экземпляра динамика наилучших ответов, начинающаяся с социального оптимума, приводит к равновесию Нэша, стоимость которого увеличивается не более чем с коэффициентом H(k) = Ө(log k).

Поиск хорошего равновесия Нэша

Сначала мы покажем, что динамика наилучших ответов в нашей задаче всегда приводит к равновесию Нэша. Заодно выясняется, что наш метод решения этой задачи также предоставляет необходимые средства для ограничения цены устойчивости.

Ключевая идея заключается в том, что общую стоимость для всех агентов не обязательно использовать как метрику прогресса, по которой ограничивается количество шагов динамики наилучших ответов. Вместо нее подойдет любая величина, которая строго убывает при обновлении пути любым агентом и которая может уменьшаться конечное количество раз. С учетом этого мы попытаемся сформулировать метрику, обладающую таким свойством. Эта метрика может быть не такой сильной, как общая стоимость с ее интуитивным смыслом, но это нормально — лишь бы она делала то, что нужно.

Для начала более подробно разберемся, почему общая стоимость агентов не подходит. Возьмем простой пример: агент t_j в настоящее время совместно использует вместе с x другими агентами путь, состоящий из одного ребра е. (Конечно, в общем случае пути агентов длиннее, но пути из одного ребра упрощают анализ данного примера.) Допустим, агент t_j решает, что для снижения стоимости стоит переключиться на путь, состоящий из одного ребра f, которое в настоящее время не используется ни одним агентом. Чтобы это произошло, должно выполняться условие c_f < c_e/(x + 1). Теперь в результате переключения общая стоимость для всех агентов возрастает на с_f; ранее x + 1 агентов вносили свой вклад в стоимость с_e, и никто не оплачивал стоимость с_f; после переключения x агентов продолжают совместно платить полную стоимость с_e, а t_j теперь оплачивает дополнительную стоимость с_f.

Чтобы рассматривать происходящее как метрику прогресса, необходимо заново определить, что же понимать под “прогрессом”. В частности, будет полезно иметь метрику, которая могла бы компенсировать дополнительную стоимость с_f некоторым выражением того, что общая “потенциальная энергия” системы снизилась на с_e/(x + 1). Это позволило бы нам рассматривать перемещение t_j как снижение суммы, так как с_f < с_e/(x + 1). Для этого можно определить для каждого ребра е “потенциал” с тем свойством, что при уменьшении количества агентов, использующих е, с x + 1 до x, этот потенциал уменьшается на с_e/(x + 1). (Соответственно потенциал должен увеличиваться на ту же величину при увеличении количества агентов, использующих е, с x до x + 1).

Интуиция подсказывает, что потенциал следует определить так, чтобы при x агентах на ребре е потенциал уменьшался на с_e/x, когда первый агент перестает использовать е; на с_e/(x - 1) — когда следующий перестает использовать е; на с_e/(x - 2) — для следующего, и т. д. Задача легко решается выбором потенциала с_e(1/x + 1/(x - 1) + ... + 1/2 + 1) = с_е ∙ H(x). Конкретнее, потенциал множества путей P₁, P₂, ..., P_k обозначается Ф(Р₁, P₂, ..., P_k) и определяется следующим образом. Пусть для каждого ребра е количество агентов, пути которых используют ребро е, обозначается x_e. Тогда

(Мы определяем гармоническое число H(0) равным 0, чтобы вклад ребер, не входящих в пути, был равен 0.)

Следующее утверждение устанавливает, что Ф действительно может использоваться в качестве метрики прогресса.

(12.14) Предположим, имеется текущее множество путей P₁, P₂, ..., P_k и агент t_j обновляет свой путь с P_j на P'_j. Тогда новый потенциал Ф(P₁, ..., P_j-1, P'_j, P_j+1, ..., P_k) строго меньше старого потенциала Ф(P₁, ..., P_j-1, P_j, P_j+1, ..., P_k).

Доказательство. Прежде чем агент t_j изменит свой путь с Р_j на Р'_j, он платит так как стоимость каждого ребра е разделяется с х_e - 1 другими агентами. После переключения он продолжает платить свою стоимость для ребер в пересечении P_j ∩ P'_j, а также платит c_j/(x_j + 1) для каждого ребра f ∈ P'_j - P_j. Таким образом, тот факт, что t_j рассматривает это переключение как улучшение, означает, что

Теперь спросим себя, что происходит с потенциальной функцией Ф. Она изменяется только на ребрах P'_j - P_j и P_j - P'_j. На первом множестве она увеличивается на

а на втором уменьшается на

Итак, тот критерий, что t_j используется для переключения путей, в точности соответствует утверждению о том, что общее увеличение строго меньше общего уменьшения, а следовательно, потенциал Ф в результате переключения пути t_j уменьшается. ■

Для каждого агента t_j существует конечное число вариантов выбора пути, и из (12.14) следует, что динамика наилучших ответов никогда не сможет вернуться к множеству путей P₁, ..., P_kпосле того, как покинет его из-за улучшающего перемещения некоторого агента. Таким образом, нам удалось показать следующее:

(12.15) Динамика наилучших ответов всегда приводит к множеству путей, образующему решение с равновесием Нэша.

Ограничение цены устойчивости

Потенциальная функция Ф также оказывается очень полезной для определения цены стабильности. Дело в том, что хотя Ф и не равна общей стоимости, сформированной всеми агентами, она достаточно близка к ней.

Чтобы убедиться в этом, обозначим C(P₁, ..., P_k) полную стоимость для всех агентов при выборе путей P₁, ..., P_k. Эта величина просто представляет собой сумму с_е по всем ребрам, входящим в объединение этих путей, поскольку стоимость каждого такого ребра полностью покрывается агентами, в пути которых оно входит.

Теперь отношение между функцией стоимости C и потенциальной функцией Ф может быть выражено следующим образом:

(12.16) Для любого множества путей P₁, ..., P_k выполняется

Доказательство. Вспомните, что ранее количество путей, содержащих ребро е, обозначалось х_е. Для сравнения C с Ф мы также определяем E⁺ как множество всех ребер, принадлежащих минимум одному из путей Р₁, ..., Р_к. Тогда по определению С имеем

Обратите внимание на простой факт: х_е ≤ k для всех е. Теперь мы просто записываем

и

Это позволяет определить границу для цены устойчивости:

(12.17) В каждом экземпляре существует решение с равновесием Нэша, для которого общая стоимость всех агентов превышает стоимость социального оптимума не более чем на множитель H(k).

Доказательство. Для получения желаемого равновесия Нэша мы начнем с социального оптимума, состоящего из путей Р*₁, ..., Р*_k, и выполним динамику наилучших ответов. Согласно (12.15), это должно привести к завершению в равновесии Нэша P₁, ..., P_k.

Во время выполнения динамики наилучших ответов общая стоимость для всех агентов может возрастать, но, согласно (12.14), потенциальная функция уменьшается. Следовательно, Ф(P₁, ..., P_k) ≤ Ф(Р*₁, ..., Р*_k).

И это практически все, что необходимо, потому что для любого множества путей величины C и Ф различаются не более чем на множитель H(k). А именно:

Итак, мы показали, что равновесие Нэша всегда существует и всегда существует равновесие Нэша, общая стоимость которого лежит в пределах множителя H(k) от социального оптимума. Пример на рис. 12.10 показывает, что в худшем случае улучшить границу H(k) не удастся.

Хотя эти утверждения очень хорошо резюмируют некоторые аспекты задачи, остается ряд вопросов, ответы на которые до сих пор неизвестны. Особенно интересен вопрос о том, возможно ли построить равновесие Нэша для этой задачи за полиномиальное время. Следует заметить, что наше доказательство существования равновесия Нэша утверждает лишь то, что в процессе перебора множества путей динамика наилучших ответов никогда не может посетить одно множество дважды, а следовательно, не может выполняться бесконечно. Однако множество возможных путей может быть экспоненциально большим, поэтому такая формулировка не дает алгоритма с полиномиальным временем. Помимо вопроса об эффективном нахождении любого равновесия Нэша, также остается открытым вопрос об эффективном нахождении равновесия Нэша, достигающего границы H(k) относительно социального оптимума в соответствии с гарантиями (12.17).

Также важно повторить один факт, уже упоминавшийся ранее: нетрудно найти задачи, для которых динамики наилучших ответов могут выполняться в бесконечном цикле и для которых равновесие Нэша может не существовать. Нам повезло, что динамика наилучших ответов могла рассматриваться как итеративное улучшение потенциальной функции, гарантирующее продвижение к равновесию Нэша, но дело в том, что такие потенциальные функции существуют не во всех задачах со взаимодействием агентов.

Наконец, интересно сравнить то, чем мы здесь занимались, с задачей, рассматривавшейся ранее в этой главе — поиском устойчивой конфигурации в сети Хопфилда. Если вы припомните обсуждение той задачи, мы анализировали процесс, в котором каждый узел “переключался” между двумя возможными состояниями, стремясь к увеличению общего веса “хороших” ребер, инцидентных ему. Это можно рассматривать как экземпляр динамики наилучших ответов для задачи, в которой у каждого узла имеется целевая функция, стремящаяся к максимизации метрики веса хороших ребер. Однако продемонстрировать схождение динамики наилучших ответов для сети Хопфилда было намного проще, чем в данном случае: тогда оказалось, что процесс переключения состояния был “замаскированной” формой локального поиска, у которого целевая функция получалась простым суммированием целевых функций всех узлов, — по сути, аналог общей стоимости для всех агентов служил метрикой прогресса. В текущем случае именно из-за того, что эта функция общей стоимости не могла служить метрикой прогресса, нам пришлось прибегнуть к более сложным средствам.