Исполнители: Робот, Чертёжник, Редактор - Элементы теории алгоритмов

Конспект

Исполнитель — любое устройство или живое существо, которое способно точно и однозначно выполнять заданные команды (действия, заданные алгоритмом).

Система команд исполнителя — совокупность команд, которые он способен выполнять.

Алгоритм — запись в той или иной форме (словесной, графической, на языке программирования) последовательности команд для исполнителя. Команды алгоритма должны соответствовать системе команд исполнителя.

Исполнитель РОБОТ — перемещается по клеткам лабиринта.

Типичная система команд:

• перемещение: вверх, вниз, влево, вправо;

• проверка наличия препятствия (стенки): сверху свободно, снизу свободно, слева свободно, справа свободно — играют роль условия;

• команда ветвления:

— выполняется команда1 (если условие истинно) или команда2 (если условие ложно), где условие — это команда проверки наличия препятствия;

• При совпадении направления проверки наличия препятствия совпадает с направлением движения Робота: ЕСЛИ <справа свободно> ТО вправо

Проверка наличия препятствия выполняется до начала движения Робота.

• При несовпадении направления проверки наличия препятствия совпадает с направлением движения Робота: ЕСЛИ <снизу свободно> ТО вправо

До начала движения Робота проверяется наличие препятствия с указанной стороны. Если оно есть, то Робот остаётся на месте. Если его нет, то начинается движение Робота в заданном направлении, даже если по направлению его движения имеется стенка (в последнем случае Робот разбивается).

• команда цикла:

или

— выполняется, пока условие истинно (условие — это команда проверки наличия препятствия).

Если в цикле ПОКА размещено несколько операторов ЕСЛИ, то:

• проверяется условие выполнения цикла; если оно ложно, то цикл не выполняется вообще;

• выполняется первый оператор ЕСЛИ (согласно заданному в нём условию);

• выполняется второй оператор ЕСЛИ (согласно заданному в нём условию);

...

• выполняется последний оператор ЕСЛИ (согласно заданному в нём условию);

• только после завершения выполнения всех операторов ЕСЛИ, записанных в теле цикла, выполняется новая проверка условия в цикле ПОКА для выяснения, должен ли цикл быть повторен.

Исполнитель Чертёжник — перемещается по координатной плоскости. Его основная команда — сместиться на (а, b), где а, b — некоторые целые числа, она перемещает Чертёжника из исходной точки с координатами (x, у) в точку с координатами (х + а, у + b).

Цикл

означает, что заданная последовательность команд выполняется указанное количество раз (значение должно быть натуральным).

Исполнитель Редактор — обрабатывает текстовые строки. Он получает на вход некоторую текстовую строку и преобразует её по заданным правилам.

Исполнитель Редактор может выполнять две команды (в них обозначения v и w обозначают некоторые последовательности — цепочки символов);

• заменить (v, w) — заменяет в строке первое встреченное при просмотре слева направо вхождение цепочки символов v на цепочку w; если же цепочка символов v в строке не найдена, выполнение данной команды не меняет строку;

• нашлось (v) — проверяет, встречается ли цепочка символов v в обрабатываемой текстовой строке, и возвращает логическое значение “истина” или “ложь”; сама текстовая строка при этом не изменяется.

Собственно алгоритм обработки текстовой строки реализуется при помощи конструкций цикла ПОКА и ветвления (ЕСЛИ ... ТО ... ИНАЧЕ).

Разбор типовых задач

Задача 1. Система команд исполнителя РОБОТ, “живущего” в прямоугольном лабиринте на клетчатой плоскости:

вверх

вниз

влево

вправо

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.

Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

сверху	снизу	слева	справа
свободно	свободно	свободно	свободно

Цикл ПОКА <условие> команда

выполняется, пока условие истинно, иначе происходит переход на следующую строку.

Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

1) 1

2) 2

3) 3

4) 4

Решение

Проще всего решить эту задачу, что называется, “в лоб”, — поочерёдно перебирая каждую клетку лабиринта и “проводя” робота из неё по маршруту согласно заданной программе. Однако такой способ требует слишком много времени, поскольку приходится проверять 36 вариантов (клеточек). Поэтому основная задача — научиться заранее отсекать заведомо неподходящие варианты, чтобы найти решение достаточно быстро (так как время на ЕГЭ ограничено).

Прежде всего следует обратить внимание: направления движения и условия остановки Робота в каждой команде ПОКА различны. Поэтому при решении такой задачи следует быть более внимательными: РОБОТ либо может остановиться, когда стенка (как условие остановки движения) появится в очередной клетке, в которую он перейдёт, с соответствующего бока, либо может разрушиться, если первой встретится стенка, перекрывающая ему путь (тогда как с соответствующего бока стенки, которая бы его остановила, нет). В условии таких задач обычно особо оговаривается факт разрушения РОБОТа, натолкнувшегося на полном ходу на стенку, хотя в данном случае оно опущено.

Далее нужно обратить внимание на то, что РОБОТ, с какой бы клеточки он ни начинал движение, однозначно останавливается (согласно программе) в клетке, где с требуемой стороны имеется стенка. Поэтому проще всего сначала определить клеточки, в которых РОБОТ должен согласно его программе завершать движение. Таких клеточек будет не так много, а дальше можно проверять каждую из них на соответствие условию: мог ли РОБОТ прийти в эту клетку, начав движение с неё же?

В данном случае РОБОТ завершает программу, если обнаруживает стенку слева.

На схеме лабиринта отмечаются все такие точки, — их оказывается всего 9 (а не 36):

Теперь они поочерёдно перебираются и проверяются, сможет ли РОБОТ, начав путь из какой-либо точки, вернуться в неё. При этом следует учесть, что если движение в каком-то направлении невозможно, так как оно изначально “запрещено” стенкой, то соответствующая строка программы пропускается, и необходимо сразу “переходим к следующей”, а если РОБОТ при движении сталкивается со стенкой, то выполнение программы прерывается, так как РОБОТ разрушился.

На рисунке ниже показаны маршруты движения РОБОТа из каждой отмеченной точки (крестиком показаны места разрушения РОБОТа при движении на стенку):

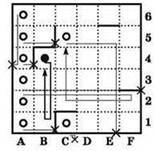
Итого, есть только одна клеточка, удовлетворяющая условию.

Ответ: 1 клеточка (вариант № 1).

В подобных задачах в командах ПОКА проверяется наличие соответствующей стенки (левой, правой, верхней или нижней) по отношению к текущей ячейке, в которой находится РОБОТ, а не по отношению к самому РОБОТу с учётом направления его движения.

Задача 2. Система команд исполнителя РОБОТ, “живущего” в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы: вверх, вниз, влево, вправо. При выполнении любой из этих команд РОБОТ перемещается на одну клетку, соответственно, вверх, вниз, влево или вправо. Четыре других команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно.

Цикл

выполняется, пока условие истинно.

В конструкции

выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ.

Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.

Сколько клеток лабиринта соответствуют требованию, что, начав движение в этой клетке и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?

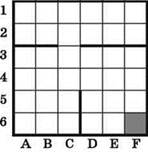
Решение

Анализируем предложенную программу РОБОТа.

• В начале очередного прохода цикла проверяется: есть ли стенки снизу и справа. Если хотя бы одно из этих направлений свободно, то выполняется очередной проход цикла. Значит, точка останова (клетка, в которой выполнение цикла корректно прекратится) имеет вид: Причём “правильной” является только одна такая клетка, а остальные две (пометим их пунктиром) — это “ловушки” для РОБОТа.

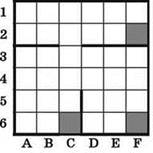
• Когда начинается очередной проход цикла, проверяется наличие стенки снизу. Если её нет, то выполняется перемещение на 1 клетку вниз. Если же стенка снизу есть, то выполняется перемещение на 1 клетку вправо, причём без проверки наличия стенки справа. Следовательно, все клетки, в которых есть стенки снизу и есть стенки справа, можно было бы сразу пометить как непригодные (начав движение из них, РОБОТ разобьётся). Но это не требуется: ведь такое условие записано в цикле ПОКА, который контролирует каждый отдельный шаг РОБОТа. (Вот если бы в цикле ПОКА было записано два или больше таких оператора ЕСЛИ, то для второго и т.д. такого оператора пришлось бы это исключение клеток сделать.)

• После выполнения одного такого хода проход цикла завершается, и вновь выполняется проверка его условия. Нетрудно понять, что в этом случае движение РОБОТа будет следующим: “идти вниз, пока это возможно (до стенки снизу), а наткнувшись на стенку снизу — пытаться уходить вправо, отыскивая проход вниз в этой стенке”.

Именно так мы и будем пытаться “трассировать” движение РОБОТа, “честно” выполняя предложенную программу. Увидев же, куда в итоге придёт РОБОТ, помечаем все пройденные клетки штриховкой (если попадаем в “ловушку”), или закрашиваем (если доходим до клетки F6). Сама же клетка F6 нам тоже подходит: если РОБОТ изначально находится в ней, то он просто никуда не пойдёт и сразу же выполнит условие задачи.

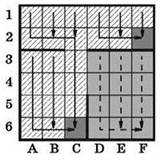
Остаётся только подсчитать количество клеточек, закрашенных зелёным: их 12.

Ответ: 12.

Задача 3. Исполнитель Чертёжник перемещается по координатной плоскости. Основная команда Чертёжника — сместиться на (а, b), где а, b — целые числа. Она перемещает Чертёжника из точки с координатами (х, у) в точку с координатами (х + а, у + b). Например, из точки с координатами (3, 5) команда сместиться на (—2, 1) переместит Чертёжника в точку (1, 6).

Цикл

означает, что заданная последовательность команд будет выполнена указанное количество раз (значение должно быть натуральным).

Чертёжник выполнял алгоритм, в котором количество повторений и оба смещения в первой из повторяемых команд неизвестны:

При этом, выполнив этот алгоритм, Чертёжник вернулся в исходную точку. Какое наибольшее количество повторений могло быть указано в конструкции “ПОВТОРИ ... РАЗ”?

Решение (способ 1)

Помните, как на физике решали задачу о движении тела, брошенного под заданным углом к горизонту (“задача о пушечном выстреле”)? Тогда мы составляли два отдельных уравнения движения по координате х и координате у и рассматривали их в виде системы из двух уравнений. В нынешней задаче нужно сделать то же самое, обозначив неизвестные нам значения переменными: k — количество повторений, х и у — неизвестные смещения в первой повторяемой команде. При этом каждое уравнение приравнивается нулю, так как Чертёжник после выполнения всех перемещений вернулся в исходную точку.

1) Перемещение Чертёжника по координате х:

2) Перемещение Чертёжника по координате у:

3) Объединяем оба уравнения в систему:

4) На первый взгляд, данная система нерешаема: два уравнения и три неизвестных. Но обратим внимание — в обоих случаях слева от знака равенства стоят произведения, один из сомножителей в которых один и тот же (&).

Разложим числа справа от знаков равенства на простые сомножители (благо это можно сделать одним- единственным способом): 21 = 3 ∙ 7; 15 = 3 ∙ 5.

Заметим: в обоих получившихся произведениях тоже повторяется один и тот же сомножитель — 3. Значит, это и есть k.

Определив, что k = 3, можно при желании (или при необходимости, если это потребуют в условии задачи) вычислить и значения хну. Нам же требуется только это значение k.

Решение (способ 2)

Можно упростить и ускорить решение, исключив составление уравнений. Для этого нужно, не обращая внимание на команды внутри цикла ПОВТОРИ, отдельно сложить только пары чисел — значений координат в командах перемещений до и после цикла:

Получаем:

• по X: -2 + (-19) = -21;

• по Y: 3 + (-18) = -15.

Полученные значения сумм берутся по модулю — получаем числа 21 и 15.

Их можно разложить на простые множители так:

21 = 3 ∙ 7,

15 = 3 ∙ 5.

Повторяется в них число 3. Это и есть значение количества повторений цикла.

Ответ: 3.

Задача 4. Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды: заменить (v, w) и нашлось (v).

Дана программа для исполнителя Редактор:

Какая строка получится из строки, состоящей из 74 идущих подряд цифр “9”?

Решение

1. Начинаем анализировать алгоритм Редактора.

Вначале имеется строка из 74 цифр “9”. Поэтому условие ПОКА истинно (три подряд девятки в этой строке есть). А вот условие ЕСЛИ — ложно (единиц в строке нет). Поэтому выполняется ветвь программы ИНАЧЕ и производится замена первых трех девяток на одну-единственную единицу:

2. На втором проходе цикла условие ПОКА всё ещё истинно (после полученной единицы имеется три девятки подряд). Условие ЕСЛИ по-прежнему ложно (трёх единиц подряд в строке пока нет). Поэтому вновь выполняется ветвь программы ИНАЧЕ и производится замена очередных трёх девяток на одну единицу:

3. На третьем проходе цикла условие ПОКА по-прежнему истинно (после двух единиц есть девятки подряд). Условие же ЕСЛИ всё ещё ложно (трёх единиц подряд в строке нет). Поэтому выполняется ветвь программы ИНАЧЕ и снова производится замена очередных трёх девяток на одну единицу:

4. На четвёртом проходе цикла условие ПОКА тоже истинно (хотя бы по первым трём единицам, образовавшимся в начале строки). А вот условие ЕСЛИ теперь истинно — у нас в начале строки имеется три подряд единицы. Поэтому теперь выполняется уже ветвь программы ТО и производится замена этих трёх единиц снова на девятку — но только на одну:

5. Делаем следующий вывод: в работе программы для исполнителя Редактор можно выделить некий “супер-цикл” — каждые четыре шага цикла ПОКА приводят к тому, что исходная строка из девяток просто уменьшает свою длину на 8 символов (было 74 девятки, а стало 66 девяток, включая только что добавленную вместо единиц). Поэтому дальнейшую работу программы можно подробно не рассматривать, а просто “отсекать” от строки по 8 девяток, пока не останется “обрубок” строки длиной 8 цифр или меньше. Поэтому начинаем вычитать из количества девяток число 8 до тех пор, пока их не останется восемь или меньше: 66 → 58 → 50 → 42 → 34 → 26 → 18 → 10 → 2.

6. А теперь снова подробно анализируем, что будет происходить с этим фрагментом. В нашем случае всё достаточно просто: у нас осталась строчка из двух девяток (“99”), для которой условие ПОКА ложно, и выполнение программы прекращается. А если получившаяся строка девяток имеет длину 3 цифры или больше, то потребуется подробно рассмотреть, какие преобразования происходят в этом фрагменте строки.

Вот, например, каким было бы окончание решения, если бы в строке осталось 5 девяток:

1) первые три девятки заменяются на одну единицу:

2) теперь в полученной строке больше нет ни трёх подряд единиц, ни трёх подряд девяток, следовательно, условие ПОКА становится ложным, и выполнение программы прекращается. А в результате остается строка “199”.

Ответ: 99.

Задача 5. Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды: заменить (v, w) и нашлось (v).

Дана программа для исполнителя Редактор:

Какая строка получится из строки, состоящей из 74 идущих подряд цифр “9”?

Единственное отличие этой задачи от предыдущей — другая запись условия ЕСЛИ: в предыдущей задаче в этом условии выполнялся поиск цифр, которых не было в исходной строке, а в данной задаче — поиск цифр, из которых и состоит исходная строка. Поэтому ход решения, хотя и будет аналогичен в обеих задачах, но совершенно различен, — как и получаемый ответ.

Решение

1. Начинаем анализировать алгоритм Редактора.

Вначале имеется строка из 74 цифр “9”. Поэтому условие ПОКА истинно (три подряд девятки в этой строке есть). Условие ЕСЛИ тоже истинно, поэтому выполняется ветвь программы ТО и производится замена первых трёх девяток на одну-единственную единицу:

2. На втором проходе цикла условие ПОКА истинно (после полученной единицы имеется три девятки подряд). Условие ЕСЛИ по-прежнему истинно. Поэтому вновь выполняется ветвь программы ТО и производится замена очередных трёх девяток на одну единицу:

3. На третьем проходе цикла условие ПОКА истинно (после двух единиц есть девятки подряд). Условие ЕСЛИ тоже всё ещё истинно. Поэтому выполняется ветвь программы ТО и снова производится замена очередных трёх девяток на одну единицу:

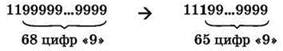
4. На четвёртом проходе цикла условие ПОКА тоже истинно. А что условие ЕСЛИ? А оно по-прежнему истинно — ведь мы ищем триады девяток, а не единицы! Поэтому по прежнему выполняется ветвь программы ТО и производится замена очередных трёх девяток на единицу:

5. Учитывая это, можно сделать вывод: при работе данной программы исполнитель Редактор просто заменяет все встреченные тройки девяток на единицы. Это будет происходить до тех пор, пока в строке ещё остаются триады девяток.

Какой станет в результате строка? Очевидно, в её начале будет столько единиц, сколько в исходной строке имелось целых триад, и это количество можно определить путём целочисленного деления: 74 DIV 3 = 24. А после них останутся “невостребованными” девятки, количество которых меньше трёх. Сколько их, модно вычислить как остаток от деления исходного количества девяток на три: 74 MOD 3 = 2. Следовательно, строка будет такой:

6. Что будет дальше? Очевидно, условие ПОКА по прежнему истинно: если нет трёх девяток подряд, то три единицы подряд в строке имеются. А вот условие ЕСЛИ по-прежнему ложно (девяток только две), поэтому на очередном проходе цикла будет выполнена ветвь ИНАЧЕ. В ней выполняется замена первых имеющихся трёх единиц на одну девятку:

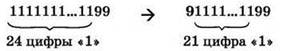
7. Условие ПОКА по-прежнему истинно. Условие ЕСЛИ тоже по-прежнему ложно (трёх девяток подряд нет), поэтому опять будет выполнена ветвь ИНАЧЕ, в которой выполняется замена очередных имеющихся трёх единиц на одну девятку:

8. Условие ПОКА истинно. Условие ЕСЛИ ложно. Поэтому вновь будет выполнена ветвь ИНАЧЕ, в которой выполняется замена очередных трёх единиц на одну девятку:

9. Условие ПОКА истинно. А вот условие ЕСЛИ теперь опять становится истинным — ведь в начале строки уже снова появились три девятки. Поэтому выполняется ветвь ТО, и выполняется замена только что получившихся трёх девяток на одну единицу:

10. Как и в предыдущей задаче, мы видим, что через каждые четыре шага цикла ПОКА полученная “промежуточная” строка из 24 единиц и оставшихся в её конце двух девяток уменьшает длину своей цепочки единиц на 8 символов (было 24 единички, а стало 16 единичек, включая только что добавленную вместо трёх девяток). Поэтому начинаем вычитать из количества единичек число 8 до тех пор, пока их не останется восемь или меньше: 16 → 8.

11. А теперь снова начинаем подробно смотреть, что происходит с нашей строкой, которая содержит 8 единичек и две девятки:

Обратим внимание: теперь в полученной строке больше нет ни трёх подряд единиц, ни трёх подряд девяток, следовательно, условие ПОКА становится ложным, и выполнение программы прекращается. А в результате остаётся строка “991199”.

На этом последнем этапе решения задачи нужно быть особенно внимательным — именно поэтому мы “вручную” вычитали восьмерки до момента, когда единиц в строке осталось 8 или меньше, а не вычисляли остаток от деления. В зависимости от количества цифр в строке, финал решения может быть различным:

• в начале строки может образоваться менее трёх девяток, а в середине — остаться менее трёх единиц (как это и произошло в нашем случае);

• преобразование единиц в девятки может оказаться полным — при этом девятки, получившиеся в начале строки, “соединятся” с девятками, которые всё время оставались в её конце, так что в строке снова окажется три подряд девятки, и нужно будет продолжить выполнение программы до тех пор, пока условие ПОКА не станет ложным.

Ответ: 991199.

Ещё раз обратим внимание: алгоритм работы Редактора различен для двух возможных вариантов его программы — ищутся ли в условии ЕСЛИ те же цифры, что уже есть в исходной строке, или цифры, которые предполагается в ней заменять. И в зависимости от этого нужно выбирать один из двух соответствующих способов решения.

Задача 6. Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды: заменить (и, w) и нашлось (и).

Дана программа для исполнителя Редактор:

На вход этой программе подается строка, состоящая из 100 цифр; последняя цифра в строке — цифра 1, а остальные цифры — шестерки. Какая строка получится в результате применения программы к этой строке?

В отличие от предыдущих задач, указанные в программе для исполнителя наборы символов теперь состоят не из одинаковых цифр.

Решение

1) Исходная строка имеет вид:

Очевидно, в ней имеется одна комбинация “661” (выделена серым), поэтому условие в операторе ПОКА истинно.

Однако условие в операторе ЕСЛИ ложно, поэтому выполняется ветвь ИНАЧЕ. В результате указанная комбинация будет заменена на “15”, а строка примет вид:

2) На втором проходе цикла (условие ПОКА по-прежнему истинно) изменение строки производится аналогично:

3) На третьем проходе цикла условие ЕСЛИ оказывается истинным — в конце строки появилась нужная комбинация “155”. Поэтому выполняется ветвь ТО, а строка получает вид:

4) Итак, после трёх шагов цикла ПОКА строка снова стала аналогичной исходной (все шестёрки и последняя единица), но её длина сократилась на три шестёрки (99 - 96 = 3).

Делаем вывод: в ходе работы программы исполнителя строка и далее будет укорачиваться — каждые три прохода цикла на три шестёрки: 96 → 93 → 90 → ...

Нетрудно догадаться, что количество шестёрок на каждом таком “промежуточном” этапе кратно 3. Проследим теперь, что происходит со строкой, когда её длина сократится до, например, семи знаков (шесть шестёрок плюс единица в конце):

5) Условие ПОКА истинно, условие ЕСЛИ ложно — выполняется ветвь ИНАЧЕ:

6) Условие ПОКА истинно, условие ЕСЛИ ложно — выполняется ветвь ИНАЧЕ:

7) Условие ПОКА истинно, условие ЕСЛИ истинно — выполняется ветвь ТО:

8) Условие ПОКА истинно, условие ЕСЛИ ложно — выполняется ветвь ИНАЧЕ:

Теперь условие ПОКА стало ложным, и выполнение программы прекращается. Оставшаяся строка и является ответом.

Ответ: 615.

В любом случае в подобной задаче мы начинаем анализировать изменения, происходящие в строке начиная с её исходного состояния, пока строка на каком-то шаге цикла не примет вид, аналогичный исходному (но став при этом короче на сколько-то цифр).

Далее мы “шагами” уменьшаем длину строки на вычисленное количество цифр, получив строку небольшой длины (но с некоторым “запасом”, например, в только что рассмотренной задаче берём строку из 6 шестёрок и единицы, а не из 3 шестёрок и единицы).

И наконец, завершаем решение, отрабатывая заданный алгоритм применительно к полученной короткой строке.