Анализ работы автомата, формирующего число по заданным правилам - Элементы теории алгоритмов

Конспект

Автомат (греч. automates — самодействующий) — самостоятельно действующее устройство (или совокупность устройств), выполняющее по заданной программе без непосредственного участия человека процессы получения, преобразования, передачи и использования энергии, материала и информации¹.

Исполнитель — субъект (человек, животное) или устройство, способное выполнить действия, предписываемые алгоритмом. При этом указанные действия выполняются формально. Исполнитель не знает о цели алгоритма, он лишь выполняет все полученные команды.

Каждый исполнитель характеризуется следующими параметрами:

— среда — условия, в которых функционирует исполнитель (например, исполнитель Черепаха имеет определённую систему координат, исполнитель Робот перемещается по клетчатому полю и т.д.);

— система команд — каждый исполнитель может выполнять команды только из некоторого строго заданного набора, где каждая команда определяет соответствующее элементарное действие.

Вспомогательные таблицы для решения задач с исполнителями — вычислителями

Система счисления	Основание (р)	Алфавит системы счисления	Пример записи числа
Двоичная	2	0, 1	1011012
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6,7	123458
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9	123410
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А (=10), В (=11), С (=12), D (=13), Е (=14), F (=15)	F4D916

Основание системы счисления	2	3	4	5	6	7	8	9
Мах цифра	1	2	3	4	5	6	7	8
Мах сумма цифр	102	113	124	135	146	157	168	179

Основание системы счисления	10	11	12	13	14	15	16
Мах цифра	9	А	В	С	D	Е	F
Мах сумма цифр	1810	1911	1A12	1В13	1C14	1D15	1E16

Разбор типовых задач

Задача 1. Автомат получает на вход два трёхзначных числа. По этим числам строится новое число по следующим правилам:

1. Вычисляются три числа — сумма старших разрядов заданных трёхзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов.

2. Полученные три числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходные трёхзначные числа: 835, 196. Поразрядные суммы: 9, 12, 11. Результат: 12119.

Определите, какое из следующих чисел может быть результатом работы автомата.

1) 151303

2) 161410

3) 191615

4) 121613

Решение

В данной задаче речь идёт о сложении цифр чисел, которые неизвестны. Пусть эти числа обозначаются как X и У и записываются в виде:

Х = х₁х₂х₃; Y = y₁y₂y₃

Суммы цифр, которые вычисляет автомат, есть:

S₁ = x₁ + y₁, S₂ = x₂ + y₂и S₃ = x₃ + y₃

Складывая цифры, оцениваются возможные значения этих сумм. Старшая цифра в двузначном числе может иметь значение от 1 до 9 (если она равна нулю, то число уже не будет трёхзначным!), а средняя и младшая — значение от 0 до 9. Тогда сумма S₁ = х₁ + у₁ может иметь значение от 2 до 18 (исходных чисел — два), а суммы S₂ = х₂ + у₂ и S₃ = х₃ + у₃ — значение от 0 до 18.

Теперь анализируются предлагаемые варианты ответов.

1. Число 151303. Оно может быть составлено из сумм 15, 13 и 03. Но третья сумма (03) имеет незначащий нуль, тогда как в условии не указано, что после сложения цифр исходных чисел автомат должен дополнять полученную сумму нулём до двузначного числа. Поэтому данный вариант ответа не может быть правильным.

2. Число 161410. Его можно представить как сочетание сумм 16, 14 и 10. Это вполне удовлетворяет условиям задачи (все три суммы входят в допустимый интервал и записаны по убыванию). Однако желательно проверить и остальные варианты.

3. Число 191615. Может быть представлено как сочетание сумм 19, 16 и 15. Однако значение суммы 19 выходит за пределы допустимого диапазона (должно быть не более 18), поэтому данный вариант числа нам не подходит.

4. Число 121613. Может быть представлено как сочетание сумм 12, 16 и 13. Эти значения соответствуют допустимому интервалу, но записаны не по убыванию. Значит, данный вариант ответа тоже ложный.

Следовательно, правильным является ответ 161410.

Ответ: число 161410 (вариант №2).

Задача 2. Устройство считывает четырёхзначное восьмеричное число и строит по нему новое число по следующему алгоритму:

1) вычисляется сумма первой и второй цифр;

2) вычисляется сумма третьей и четвёртой цифр;

3) эти суммы записываются друг за другом без разделителей по убыванию.

Пример. Задано число 7145. Суммы:

7 + 1 = 10; 4 + 5 = 11. Результат: 1110.

Какое из чисел может быть результатом работы такого устройства.

1) 119

2) 1213

3) 1411

4) 1715

Решение

Вычисления производятся в недесятичной системе счисления.

Пусть неизвестные цифры числа обозначаются как х, у, z и t. Подразумевается, что само число тогда имеет вид: xyzt.

Суммы цифр, которые вычисляет автомат, — это:

S₁ = х + у и S₂ = z + t

Складывая восьмеричные цифры, которые могут меняться от 0 до 7, оцениваются возможные значения этих сумм. Тогда, согласно правилам восьмеричной арифметики, сумма двух таких цифр может меняться от 0 до 7₈ + 7₈ = 16₈.

Теперь просматриваются предлагаемые варианты ответов.

1. Число 119. Можно представить его как 11 и 9 или как 1 и 19. Однако ни один из этих вариантов записи нам не годится: в первом случае восьмеричная запись суммы не может содержать цифры больше 7, а во втором число 19 не может быть суммой двух восьмеричных цифр.

2. Число 1213. Его можно представить как 12 и 13. Оба эти числа могут быть суммами восьмеричных цифр (так как удовлетворяют допустимому диапазону значений таких сумм). Однако они записаны по возрастанию (а не по убыванию, как требуется в условии задачи). Поэтому данное число не может быть решением.

3. Число 1411. Его можно представить как 14 и 11. Обе эти составляющие могут быть значениями сумм восьмеричных цифр, записаны они по убыванию. Значит, это число может быть решением данной задачи.

4. Число 1715. Может быть представлено как 17 и 15. Поскольку его первая составляющая (17) превышает максимально возможное значение суммы, данное число не может быть решением задачи.

Следовательно, единственный вариант ответа, который может быть результатом работы описанного в задаче автомата, — это число 1411.

Ответ: число 1411 (вариант ответа №3).

Задача 3. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.

2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходное число: 6531. Суммы: 6 + 5 = 11, 3 + 1 = 4. Результат: 411.

Укажите наибольшее число, в результате обработки которого автомат выдаст число 1113.

Решение

Подобные задачи уже были рассмотрены выше. Но раньше нужно было выбрать подходящие числа из приведённых вариантов ответа, а теперь, наоборот, искать такое число.

1) Числа (по умолчанию) десятичные. Значит, суммы цифр могут быть в диапазоне от 1 (1+0) до 18 (9+9).

2) Автомат выдал число 1113. Значит, оно состоит из двух значений сумм, записанных по возрастанию: 11 и 13.

3) Число 11 может быть суммой цифр: 2+9, 3+8, 4+7 или 5+6. Число 13 может быть суммой цифр: 4+9, 5+8, 6+7. Значит, пары цифр в исходном числе могут быть такими: одна пара — 29, 92, 38, 83, 47, 74, 56, 65 и другая пара — 49, 94, 58, 85, 67, 76 (ведь соответствующие цифры могут меняться местами в соответствующих суммах).

4) Наибольшим является число, в которое входят наибольшие цифры, причём они по возможности располагаются слева направо по убыванию (поскольку чем старше разряд, тем больше “вес” цифры). Тогда из доступных нам “для конструирования” наборов пар цифр выберем две наибольшие (по одной из каждого набора): 92 и 94 и запишем их по убыванию: 9492.

Ответ: 9492.

Задача 4. Автомат получает на вход трёхзначное число. По этому числу формируется новое число по следующим правилам.

1. Складываются первая и вторая, а затем — вторая и третья цифры исходного числа.

2. Полученные два числа записываются друг за другом подряд в порядке возрастания.

Пример. Исходное число: 176. Полученные числа: 1 + 7 = 8, 7 + 6 = 13. Результат: 813.

Найдите наибольшее исходное число, для которого автомат выдаст результат 815.

Решение

Сначала определим, как можно “разрезать” результирующее число на два, вычисленных автоматом.

Вспомним, что сумма двух десятичных цифр (которые могут быть равны от 0 до 9) может равняться от 0 (0+0) до 18 (9+9).

Если пытаться разделить число 815 как 81 и 5, то первое из этих чисел не соответствует этому возможному диапазону значений сумм цифр (да к тому же тогда числа записаны не по возрастанию). Поэтому остается только один вариант: число 815 как 8 и 15.

Теперь посмотрим, какие цифры могут давать такие суммы:

• 8 = 0 + 8, 1 + 7, 2 + 6, 3 + 5, 4 + 4;

• 15 = 9 + 6, 8 + 7.

А теперь — самое главное. По условию, одна сумма — это сумма первой и второй цифры исходного числа, а вторая — это сумма второй и третьей цифры. Вторая цифра, таким образом, должна повторяться в обеих суммах.

Ищем такие две суммы в обеих “подборках” (для числа 8 и для числа 15).

Это пары: 0 + 8 и 8 + 7; 1 + 7 и 8 + 7; 9 + 6 и 2 + 6.

Им соответствуют числа (учитывая, что нуль не может быть записал самым первым — тогда он был бы незначащим, а число — двузначным): 780, 178, 871, 962, 269 (везде повторяющаяся цифра стоит в середине).

Остаётся найти среди них наибольшее. Очевидно, это число 962.

Ответ: 962.

Задача 5. Процессор получает пятизначное число и по нему вычисляет новое, используя следующие правила:

1) отдельно суммируются первая, третья и пятая цифры, а также вторая и четвёртая цифры;

2) два полученных числа записываются подряд по неубыванию.

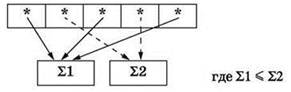
Требуется определить наименьшее возможное число, при обработке которого будет получен результат 621.

Решение

1. Сумма трёх десятичных цифр может иметь значение от 1 (“1+0+0”, причём первая цифра числа — всегда ненулевая!) до 27 (“9+9+9”). Сумма двух десятичных цифр может иметь значение от 0 (“0+0”) до 18 (“9+9”).

2. Анализируем число 621. Это может быть “6 и 21” либо “62 и 1”. Но условию записи чисел в порядке неубывания соответствует только пара 6 и 21.

3. Так как сумма двух цифр не может быть равна 21, можно сделать вывод: сумма 1-й, 3-й и 5-й цифр исходного числа равна 21, а сумма 2-й и 4-й цифр равна 6.

4. Чтобы исходное число было наименьшим из возможных, в нём цифры должны быть записаны слева направо по возрастанию. Таким условиям соответствует число 30969:

Рассуждения при “конструировании” этого числа следующие:

• для 2-й и 4-й цифр вторую цифру (более левую) выбираем минимально возможной — равной 0, тогда 4-я цифра равна 6;

• для 1-й, 3-й и 5-й цифр тоже стараемся взять первую цифру минимально возможной: это 3, так как тогда на сумму 3-й и 5-й цифр остается 18 — максимально возможное значение суммы 2 цифр; тогда остается взять 3-ю и 5-ю цифры равными 9.

Ответ: 30969

---

¹ Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.