Информатика: Новый полный справочник для подготовки к ЕГЭ - 2018 год
Решение систем логических уравнений - Основы логики
Конспект
В алгебре логики изучаются логические операции, производимые над высказываниями. Такие высказывания могут быть истинными или ложными. Применяя к простым высказываниям логические операции, можно строить составные высказывания.
Основные логические операции
• Отрицание (инверсия, логическое НЕ)
Смысл операции: результат меняется на противоположный (вместо истины — ложь, вместо лжи — истина).
Обозначение: ¬.
Таблица истинности:
|
А |
¬А |
|
0 |
1 |
|
1 |
0 |
• Логическое сложение (дизъюнкция, логическое ИЛИ)
Смысл операции: результат — истина, если хотя бы один операнд — истина (операндом называется то значение или та переменная, над которым (которой) осуществляется операция).
Обозначения: V или +.
Таблица истинности:
|
А |
В |
А V В |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
• Логическое умножение (конъюнкция, логическое И)
Смысл операции: результат — истина, если оба операнда — истина.
Обозначения: Λ или &.
Таблица истинности:
|
А |
В |
А Λ В |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
• Исключающее ИЛИ (сложение по модулю 2, строгая дизъюнкция)
Смысл операции: результат — истина, если операнды различны.
Обозначения: ⊕ или ≠.
Таблица истинности:
|
А |
В |
А ⊕ В |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
• Следование (импликация)
Смысл операции: из лжи может следовать что угодно, а из истины — только истина.
Обозначение: →.
Таблица истинности:
|
А |
В |
А → В |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
• Равносильность (эквиваленция)
Смысл операции: результат — истина, если операнды одинаковы.
Обозначения: = или ↔.
Таблица истинности:
|
А |
В |
А ↔ В |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Если в логическом выражении используется несколько логических операций, то их порядок определяется приоритетами логических операций:

Операцию “импликация” можно выразить через “ИЛИ” и “НЕ”:
![]()
Операцию “эквиваленция” также можно выразить через “ИЛИ” и “НЕ”:
![]()
Поразрядные (побитовые) логические операции
Кроме обычных логических операций, применимых по отношению к логическим переменным, возможны поразрядные (побитовые) логические операции, выполняемые для пар “одноименных” (соответствующих одним и тем же разрядам) битов двух целых чисел. При этом двоичное значение 1 рассматривается как “истина”, а значение 0 — как “ложь”. Результатом выполнения поразрядной логической операции является целое число.
• Поразрядная конъюнкция
Для каждой пары битов выполняется логическая операция “И”.
Пример:
![]()
• Поразрядная дизъюнкция
Для каждой пары битов выполняется логическая операция “ИЛИ”.
Пример:
![]()
Основные законы алгебры логики
|
Законы коммутативности |
|
|
Законы ассоциативности |
|
|
Законы дистрибутивности |
|
|
Закон непротиворечия (высказывание не может быть одновременно истинным и ложным) |
|
|
Закон исключения третьего (либо высказывание, либо его отрицание должно быть истинным) |
|
|
Закон двойного отрицания |
|
|
Законы де Моргана |
|
|
Законы рефлексивности (идемпотенции) |
|
|
Свойства логических констант 1 и 0 |
|
|
Законы поглощения |
|
Полезно запомнить следующее правило: если известно количество решений уравнения F(x1, х2, ... хn) = 1, то количество возможных решений “противоположного” уравнения F(x1, х2, ... хn) = 0 равно разности количества всех возможных комбинаций значений переменных х1, х2,... хn (которое равно 2n) и количества решений уравнения F(x1, х2, ... хn) = 1 (и, соответственно, наоборот):
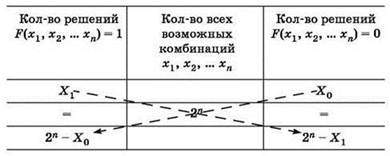
Это правило легко доказать, рассмотрев полную таблицу истинности логической функции F(x1, х2, ... хn): если исключить из нее строки, соответствующие значению F = 1, то останутся строки, соответствующие значению F = 0,и наоборот.
Разбор типовых задач
Задача 1. Сколько различных решений имеет система уравнений
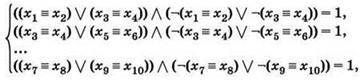
где x1, х2, ..., х10 — логические переменные?
В ответе не нужно перечислять все различные наборы значений х1, х2, ..., х10, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение
1) Анализируется первое уравнение:
![]()
Последняя выполняемая операция здесь — И, поэтому:
![]()
Следует обратить внимание: в обеих частях записаны одни и те же тождества, только в первом случае они записаны “как есть”, а во втором — с отрицаниями. Тогда, если (х1 ≡ х2) = 1 и (х3 ≡ х4) = 1, то первая запись будет истинной, но тогда ¬(x1 ≡ х2) и ¬(х3 ≡ х4) оба будут ложными, и вторая запись ложна. И наоборот, при (х1 ≡ х2) = 0 и (х3 ≡ х4) = 0 первая запись будет ложной, а вторая (с отрицаниями) — истинной. Не подходит ни тот, ни другой вариант. “Спасает положение” то, что тождества в обеих записях соединены операцией ИЛИ, т.е. оба раза достаточно, чтобы единице было равно хотя бы одно из этих тождеств.
Вывод: чтобы первое уравнение системы было равно 1, нужно, чтобы либо (х1 ≡ х2) = 1 и (х3 ≡ х4) = 0, либо, наоборот, (х1 ≡ х2) = 0 и (х3 ≡ х4) = 1.
Первое из этих “либо” даёт такие варианты значений переменных, когда х1 и х2 одинаковы, а х3 и х4 различны:
(0, 0, 1, 0)
(0, 0, 0, 1)
(1, 1, 1, 0)
(1, 1, 0, 1)
Второе “либо”, аналогично, даёт варианты, в которых, наоборот, х1 и х2 различны, а х3 и х4 одинаковы:
(1, 0, 0, 0)
(0, 1, 0, 0)
(1, 0, 1, 1)
(0, 1, 1, 1)
Всего — 8 вариантов.
2) Добавляется в анализ второе уравнение:
![]()
Рассуждая аналогично и учитывая, что для х3 и х4 возможные варианты “унаследованы” от предыдущего уравнения, получается, что в вариантах значений х5, х6, добавленных этим вторым уравнением, для одинаковых значений х3 и х4 должны быть разными значения х5 и х6, а для различных значений х3 и х4 — одинаковые значения х5 и х6:

Итого из 8 предыдущих вариантов благодаря второму уравнению получается 16 (вдвое больше).
3) Очевидно, такая тенденция сохранится и дальше, ведь уравнения системы — типовые. Значит, добавление в рассмотрение третьего уравнения, пропущенного в записи системы и использующего переменные х5, х6, х7, x8, снова удвоит количество вариантов значений переменных: из 16 их получится 32.
Аналогично, последнее, четвёртое уравнение системы (переменные х7, х8, х9, х10) снова удваивает количество вариантов, “унаследованное” от предыдущего уравнения. В итоге для всей системы уравнений получается 64 возможных варианта значений переменных x1 - x10.
Ответ: 64 варианта значений переменных.
Задача 2. Сколько существует различных наборов значений логических переменных x1, х2, х3, х4, х5, у1, у2, у3, у4, у5, которые удовлетворяют всем перечисленным ниже условиям?
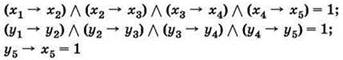
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, y1, у2, у3, у4, у5, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение
Как и всегда при решении задач с системами логических уравнений, нужно сначала проанализировать каждое уравнение в отдельности. При этом, первое и второе уравнения заданной системы практически идентичны (с точностью до имён переменных — “игреки” вместо “иксов”), и это существенно облегчает работу.
Анализируя первое уравнение:
![]()
Таблица истинности логической операции следования: единственная ситуация, при которой её результат равен нулю, — когда из единицы следует нуль, а во всех других случаях эта операция возвращает единицу:
|
а |
b |
а → b |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Кроме того, поскольку все отдельные операции следования в первом уравнении соединены операцией И, для выполнения заданного в нём равенства требуется, чтобы все операции следования давали в результате единицу.
Чтобы найти все возможные комбинации значений переменных, задействованных в первом уравнении, удобнее всего выполнить построение дерева решений: это позволит не запутаться и не пропустить какие-то варианты. При построении дерева на каждом его очередном шаге анализируется очередная пара переменных и для каждой имеющейся ветви определяются дальнейшие варианты ветвления. Слева указываются логические операции следования, которые и анализируются на соответствующих шагах (уровнях дерева). Ключевым моментом при построении дерева является уже отмеченный выше факт, что для получения единичного результата из нуля может следовать любое значение второй переменной, а из единицы — только единица.
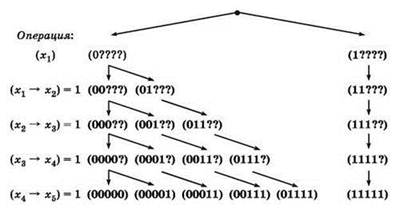
Основную идею при построении данного дерева можно условно выразить фразой: “размножаются только нули”. То есть если имеется начало набора значений пяти переменных, которое на данный момент завершается нулём, то продолжить его можно как нулём, так и единицей (в дереве имеется ветвление), но если текущая последовательность заканчивается единицей, то продолжать её можно только единицей, и в дереве не будет никакого ветвления, а только продолжение уже существующей ветви.
Полный набор возможных значений переменных, удовлетворяющих первому уравнению, тогда содержится в самой нижней строке построенного дерева (в его “листьях”): (х1х2х3х4х5) = (00000), (00001), (00011), (00111), (01111), (11111).
Второе уравнение по структуре полностью совпадает с первым. Поэтому анализировать его нет необходимости, и можно сразу записать набор возможных для него значений переменных: (y1y2y3y4y5) = (00000), (00001), (00011), (00111), (01111), (11111).
Если бы в условии задачи присутствовали только рассмотренные два уравнения, то, поскольку в них нет общих переменных, решением этой системы уравнений были бы все возможные попарные сочетания найденных наборов значений “иксов” и “игреков”. Именно третье уравнение, в котором одной логической операцией связаны один из “иксов” и один из “игреков”, является “ключом”, определяющим выбор: какие из найденных комбинаций наборов значений (х1х2х3х4х5) и (y1y2y3y4y5) подходят, а какие — нет.
Запись этого третьего уравнения:
y5 → x5 = 1
Согласно ему, из всех найденных пар наборов значений “иксов” и “игреков” для решения подходят только такие, в которых значения указанных переменных соответствуют истинности заданной логической операции, т.е.:
• когда в наборе значений (y1y2y3y4y5) пятая цифра равна нулю, в пару с ним годятся любые наборы значений (х1х2х3х4х5), поскольку, что бы в них ни стояло в пятой позиции (0 или 1), результат операции у5→ х5 = 1 в любом случае будет равен 1 (см. таблицу истинности для этой операции);
• когда в наборе значений (y1y2y3y4y5) пятая цифра равна единице, в пару с ним годятся только такие наборы значений (х1х2х3х4х5), в которых пятая цифра равна 1.
Удобнее и нагляднее всего расписать все получаемые комбинации значений х и y виде таблицы (“матрицы решений”). Анализируемые цифры в ней выделены подчеркиванием.
|
(y1y2y3y4y5) |
(x1x2x3x4x5) |
Кол-во вариантов (пар) |
|||||
|
(00000) |
(00001) |
(00011) |
(00111) |
(01111) |
(11111) |
||
|
(00000) |
+ |
+ |
+ |
+ |
+ |
+ |
6 |
|
(00001) |
- |
+ |
+ |
+ |
+ |
+ |
5 |
|
(00011) |
- |
+ |
+ |
+ |
+ |
+ |
5 |
|
(00111) |
- |
+ |
+ |
+ |
+ |
+ |
5 |
|
(01111) |
- |
+ |
+ |
+ |
+ |
+ |
5 |
|
(11111) |
- |
+ |
+ |
+ |
+ |
+ |
5 |
|
Всего возможных вариантов (пар) наборов значений (х1х2х3х4х5) и (y1y2y3y4y5): |
31 |
||||||
Ответ: заданная система уравнений имеет 31 решение.
Таким образом, в данной задаче система логических уравнений состоит из двух чётко обособленных частей: первые два уравнения представляют собой “генераторы наборов значений переменных”, а последнее уравнение — это “селектор”, “фильтр”, осуществляющий отбор из всех возможных попарных комбинаций наборов “иксов” и “игреков”.
Задача 3. Сколько существует различных наборов значений логических переменных х1, х2, ..., х9, х10, которые удовлетворяют всем перечисленным ниже условиям?
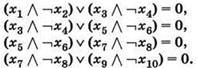
В ответе не нужно перечислять все различные наборы значений x1, х2, ..., х9, х10, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение
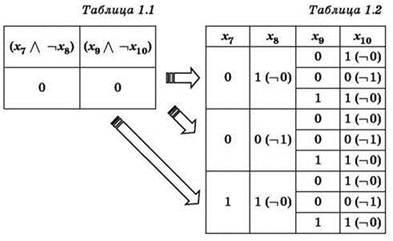
1. Анализ начинается с последнего уравнения:
![]()
Это уравнение состоит из двух операндов (скобок), соединённых логической операцией ИЛИ. Результат выполнения операции ИЛИ равен нулю в единственном случае — если оба операнда равны нулю. Тогда:
![]()
Анализируются все возможные варианты значений переменных х7, х8, х9, х10, удовлетворяющие этим условиям, и составляется таблица. При этом учитывается, что логическая операция И даёт нулевой результат в трёх случаях — когда хотя бы одна переменная равна нулю или обе переменные равны нулю, и для каждого такого случая для первой пары переменных возможно по три случая для второй пары переменных. Кроме того, нужно учитывать, что переменные х8 и х10 записаны с отрицаниями, поэтому в таблицу нужно записывать противоположные значения.
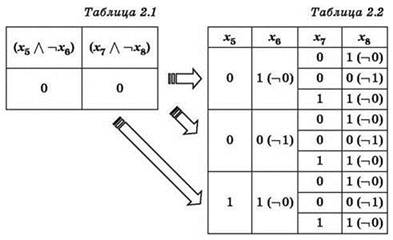
2. Аналогично анализируется предпоследнее уравнение: ![]()
Это уравнение также состоит из двух операндов, соединённых логической операцией ИЛИ, которая даёт нулевой результат, если оба операнда равны нулю:
![]()
Так же, как для последнего уравнения, записываются в таблицу все возможные варианты значений переменных х5, х6, х7, х8, удовлетворяющие этим условиям. Поскольку структура обоих рассмотренных уравнений одинакова, заполнение таблицы будет точно таким же.
Для всех четырёх уравнений структура и заполнение таблицы возможных значений четырёх используемых в каждом уравнении переменных одна и та же. Смысл решения задачи проявляется во взаимосвязи между этими таблицами, отражающими взаимосвязь между уравнениями.
Следует обратить внимание, что переменные х7 и x8 используются в обоих рассмотренных уравнениях. Поэтому для каждого варианта (набора значений) переменных х7 и x8, приведённого в таблице 2.2, нужно определить количество наборов переменных х7, х8, х9, х10, имеющихся в таблице 1.2.
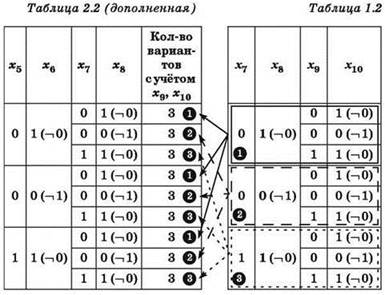
3. Аналогично анализируется второе по счёту уравнение: ![]()
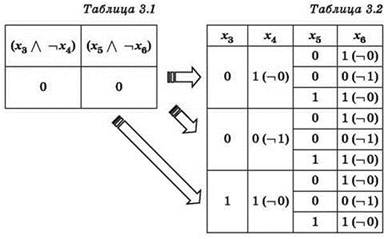
Переменные х5 и х6 используются в двух рассмотренных уравнениях (втором и третьем), поэтому для каждого варианта (набора значений) переменных х5 и х6 в таблице 3.2 нужно определить количество наборов переменных х5, х6, х7, х8, имеющихся в таблице 2.2 (с учётом ранее определённых количеств вариантов для х7, х8).
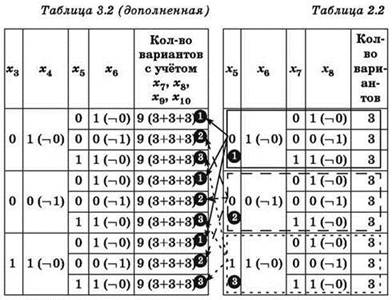
4. Аналогично анализируется первое уравнение: ![]()
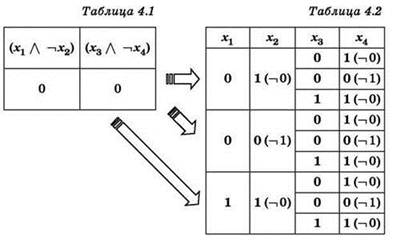
Переменные х3 и х4 используются в двух уравнениях (первом и втором), поэтому для каждого варианта (набора значений) переменных х3 и х4 в таблице 4.2 нужно определить количество наборов переменных х3, х4, х5, х6, имеющихся в таблице 3.2 (с учётом ранее определённых количеств вариантов для х5, х6).
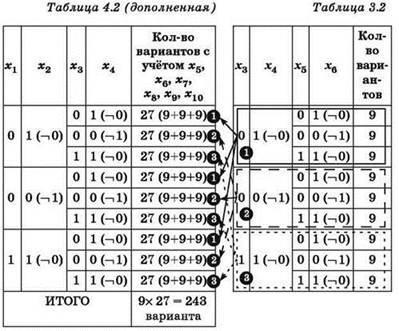
Ответ: 243 варианта.
Задача 4. Сколько существует различных наборов значений логических переменных a1, а2, ..., а5, b1, b2, ..., b5, c1, с2, ..., с6, которые удовлетворяют перечисленным уравнениям?
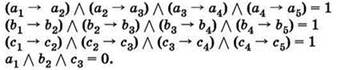
В качестве ответа нужно указать количество таких наборов переменных.
Решение
1) Анализируем первое уравнение:
![]()
Начинаем составлять таблицу возможных значений переменных a1, а2, ..., а5. При этом учитываем, что при использовании логической операции “И” результат 1 обеспечивается только единичными значениями всех её аргументов, а также помним, что операция следования истинна в трёх случаях: 1 → 1, 0 → 1 и 0 → 0. Поэтому если в каждом следовании первая переменная равна единице, то из неё может следовать только единица, а из нуля может следовать как единица, так и нуль. В результате получаем следующую таблицу значений переменных:
|
a1 |
a2 |
a3 |
a4 |
a5 |
|
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
2) Второе уравнение полностью аналогично первому, только имена переменных другие. Поэтому таблица значений переменных будет такая же. И то же самое можно сказать про третье уравнение. Получаем:
|
b1 |
b2 |
b3 |
b4 |
b5 |
c1 |
c2 |
c3 |
c4 |
c5 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3) Анализируем четвёртое уравнение. Оно является “ключевым”:
![]()
Строим для него таблицу истинности:
|
a1 |
b2 |
c3 |
Результат |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Из неё нам требуются все строки, кроме последней.
4) Подсчитаем теперь количества значений переменных, соответствующие таблице истинности четвёртого уравнения. Для этого в таблицах значений переменных первых трёх уравнений выделяем столбцы, соответствующие переменным a1, b2 и с3:
|
a1 |
a2 |
a3 |
a4 |
a5 |
b1 |
b2 |
b3 |
b4 |
b5 |
c1 |
c2 |
c3 |
c4 |
c5 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
||
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
||
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
И теперь для каждой строки таблицы значений четвёртого уравнения перемножаем друг на друга количества нулей и единиц соответственно, содержащихся в выделенном столбце для каждой из переменных:
|
a1 |
b2 |
c3 |
Кол-во наборов переменных |
|
0 |
0 |
0 |
5 ∙ 4 ∙ 3 = 60 |
|
0 |
0 |
1 |
5 ∙ 4 ∙ 3 = 60 |
|
0 |
1 |
0 |
5 ∙ 2 ∙ 3 = 30 |
|
0 |
1 |
1 |
5 ∙ 2 ∙ 3 = 30 |
|
1 |
0 |
0 |
1 ∙ 4 ∙ 3 = 12 |
|
1 |
0 |
1 |
1 ∙ 4 ∙ 3 = 12 |
|
1 |
1 |
0 |
1 ∙ 2 ∙ 3 = 6 |
|
Итого: |
60 + 60 + 30 + 30 + 12 + 12 + 6 = 210 |
||
Ответ: 210.
Задача 5. Обозначим через & поразрядную конъюнкцию неотрицательных целых чисел. Для какого наименьшего неотрицательного целого числа Р формула
![]()
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной А)?
Решение (1 способ)
1. Преобразуем заданное логическое выражение, чтобы заменить операцию следования на операции И, ИЛИ, НЕ. Кроме того, используем квадратные скобки, чтобы сделать запись выражения более понятной.
![]()
![]()
2. Отрицанием операции сравнения “равно” является операция сравнения “не равно”, и наоборот, отрицанием операции сравнения “не равно” является операция сравнения “равно”. Кроме того, мы можем убрать из выражения круглые скобки, так как используемые в нём операции равноправны.
![]()
3. Нам нужно, чтобы при любом значении А значение этого выражения было истинным. При использовании операции “ИЛИ” для этого достаточно, чтобы был истинным хотя бы один операнд.
При преобразовании заданных десятичных чисел в двоичные нужно всегда использовать наибольшее получаемое количество разрядов (при необходимости добавляя слева незначащие нули), и точно такое же количество разрядов рассматривать для чисел А и Р.
1) Операция поразрядной конъюнкции А & 61:
![]()
Если в числе А биты в разрядах 0, 2, 3, 4 и 5 равны нулю, то этого достаточно для истинности всего выражения в целом, тогда как бит в разряде 1 может быть любым:

2) Операция поразрядной конъюнкции А & 49:
![]()
Чтобы результат данной поразрядной конъюнкции был не равен нулю, в числе А хотя бы один из битов в разрядах 0, 4 и 5 обязательно должен иметь значение 1.

4. Получаем следующий набор условий, которые определяют истинность заданного выражения (зачеркнутые ячейки соответствуют битам, значения которых безразличны):
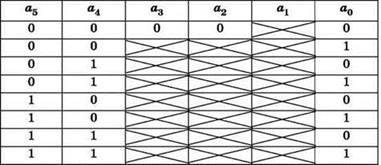
Какая ситуация является “критичной” для истинности выражения (т.е. требуется обязательная истинность третьего операнда — А & Р ≠ 0?
Очевидно, это происходит тогда и только тогда, когда все три бита в разрядах 0, 4 и 5 имеют значения 0, а хотя бы один бит в разрядах 2 или 3 равен 1.
Все другие варианты значений битов 0, 4 и 5 сразу гарантируют истинность выражения благодаря второму операнду, а при нулевых битах 0, 4 и 5 и обоих нулевых битах 2 и 3 гарантирована истинность выражения благодаря первому операнду.
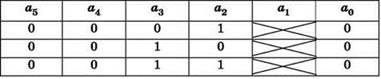
5. Операция поразрядной конъюнкции А & Р:
![]()
Для найденных нами трёх “критичных” случаев получаем ситуации:

Чтобы гарантированно обеспечить неравенство данной операции поразрядной конъюнкции, тем самым истинность третьего операнда и благодаря этому — истинность всего выражения, необходимо, чтобы было выполнено условие: в числе Р оба бита в разрядах 2 и 3 равны 1.
Мы не знаем заранее, каковы будут биты 2 и 3 в числе А, — знаем только, что хотя бы один из них — ненулевой. Поэтому если в числе Р выбрать равным 1 только один бит — второй или третий, то может возникнуть ситуация, что этот единичный бит будет “погашен” нулевым битом в числе А, и данный операнд останется ложным.
Если в числе Р оба бита в разрядах 2 и 3 будут равны 0, то может ли “спасти ситуацию” какое-либо значение бита 1 в числе Р? Очевидно, нет: даже если этот бит в числе Р равен 1, это не гарантирует получение не равного нулю результата, так как в числе А бит в разряде 1 может оказаться нулевым.
6. Зная, что в числе Р оба бита в разрядах 2 и 3 обязательно должны быть равны 1, и что это единственное условие (т.е. остальные биты числа Р могут быть любыми), получаем, что Р может быть равно: 001100, 001101, 001110, 001111.
Нам требуется определить наименьшее возможное (неотрицательное) значение Р. Таковым является значение 0011002 = 12.
Ответ: 12.
Решение (2 способ)
1. Преобразуем заданное логическое выражение, чтобы заменить операцию следования на операции И, ИЛИ, НЕ. Используем квадратные скобки, чтобы сделать запись выражения более понятной.
![]()
2. Отрицанием операции сравнения “равно” является операция сравнения “не равно”, и наоборот, отрицанием операции сравнения “не равно” является операция сравнения “равно”. Кроме того, убираем из выражения круглые скобки.
![]()
3. Нам нужно, чтобы при любом значении А значение этого выражения было истинным. При использовании операции “ИЛИ” для этого достаточно, чтобы был истинным хотя бы один операнд.
4. Рассмотрим операцию поразрядной конъюнкции А & 61. Представим число 61 как сумму степеней двоек: 61 = 32 + 16 + 8 + 4 + 1 (6110 = 1111012).
Тогда, чтобы результат поразрядной конъюнкции А & 61 был равен нулю, необходимо соблюсти условие: A ∉ {1, 4, 8, 16, 32} (т.е. в числе А не должно быть таких единичных битов, которые формируют указанные степени двойки).
5. Рассмотрим операцию поразрядной конъюнкции А & 49. Представим число 49 как сумму степеней двоек: 49 = 32 + 16 + 1 (4910 = 1100012).
Тогда, чтобы результат поразрядной конъюнкции А & 49 не был равен нулю, необходимо соблюсти условие: А ∈ {1, 16, 32} (т.е. в числе А должен быть хотя бы один такой единичный бит, который формирует указанные степени двойки).
6. Итак, в ситуациях, когда А ∉ {1, 4, 8, 16, 32} ИЛИ А ∈ {1, 16, 32}, заданное выражение гарантированно истинно. Нас же интересует обратная ситуация, когда истинность обеспечивается условием А & Р ≠ 0 и, соответственно, А е {1, 4, 8, 16, 32} И А ∉ {1, 16, 32}, то есть: А ∈ {4, 8}. Тогда Р = 8 + 4 = 12.
Ответ: 12.
Мнемоническое правило: если в рассматриваемом условии записано равенство, то оно соответствует непринадлежности множеству чисел-степеней двойки. И наоборот, неравенству соответствует принадлежность множеству чисел-степеней двойки.
Для условия А & Р ≠ 0 рассматривается обратная ситуация истинности условий.
Задача 6. Обозначим через & поразрядную конъюнкцию неотрицательных целых чисел. Для какого наибольшего натурального числа Р формула
![]()
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной А)?
Задача отличается от предыдущей иным порядком следования операндов (условий сравнения) в заданном логическом выражении и поиском наибольшего соответствующего условиям задачи числа.
Решение
1. Преобразуем заданное логическое выражение, чтобы заменить операцию следования на операции И, ИЛИ, НЕ. Используем квадратные скобки, чтобы сделать запись выражения более понятной.
![]()
2. Отрицанием операции сравнения “равно” является операция сравнения “не равно”, и наоборот, отрицанием операции сравнения “не равно” является операция сравнения “равно”. Кроме того, убираем из выражения круглые скобки.
![]()
3. Нам нужно, чтобы при любом значении А значение этого выражения было истинным. При использовании операции “ИЛИ” для этого достаточно, чтобы был истинным хотя бы один операнд.
4. Рассмотрим операцию поразрядной конъюнкции А & 12. Представим число 12 как сумму степеней двоек: 12 = 8 + 4 (1210 = 11002).
Тогда, чтобы результат поразрядной конъюнкции А & 12 не был равен нулю, необходимо соблюсти условие: А ∈ {8, 4} (т.е. в числе А должен быть хотя бы один такой единичный бит, который формирует указанные степени двойки).
5. Рассмотрим операцию поразрядной конъюнкции А & 68. Представим число 68 как сумму степеней двоек: 68 = 64 + 4 (6810 = 10001002).
Тогда, чтобы результат поразрядной конъюнкции А & 68 не был равен нулю, необходимо соблюсти условие: А ∈ {64, 4} (т.е. в числе А должен быть хотя бы один такой единичный бит, который формирует указанные степени двойки).
6. Итак, в ситуациях, когда А ∈ {8, 4} ИЛИ А ∈ {64, 4}, заданное выражение гарантированно истинно. Пас же интересует ситуация, когда истинность обеспечивается условием А & Р = 0. Ему соответствует та же самая запись А ∈ {8, 4} ИЛИ А ∈ {64, 4}, то есть: А ∈ {64, 8, 4}. Тогда Р = 64 + 8 + 4 = 76.
Последнее рассуждение легко понять, если учесть следующее. Ранее мы показали, что истинность выражения гарантирована, если в числе А есть хотя бы один такой единичный бит, который формирует соответствующие степени двойки. Тогда нас интересует обратная ситуация — когда все указанные биты равны нулю (а состояние остальных битов безразлично). И в этой ситуации требуется найти наибольшее число Р, при котором соблюдается истинность условия А & Р = 0. Но раз все указанные биты в числе А — нулевые, а состояние остальных битов безразлично, мы для получения наибольшего возможного числа Р просто выбираем все указанные биты в числе Р равными 1 (так как все равно они будут “погашены в нули” соответствующими нулевыми битами числа А).
Ответ: 76.