ИГРОВЫЕ ЛОГИЧЕСКИЕ ЗАДАЧИ - РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ ЗАНЯТИЙ С ИСПОЛЬЗОВАНИЕМ ДИДАКТИЧЕСКИХ МАТЕРИАЛОВ

Цель: научить учащихся находить выигрышную стратегию в игровых логических задачах.

Основное содержание

1. Изучаем выигрышную стратегию для игровой задачи с камнями.

2. Учимся находить выигрышные стратегии для игровых задач.

Формы, методы и средства

Игровой и исследовательский методы, самостоятельная работа в группах. Оборудование: мультимедийный проектор, компьютер.

Проведение занятия

1. Знакомим учащихся с задачами-играми (игра “Крестики-нолики”, игра “Рендзю”, игровые задачи с камнями) и проводим исторический экскурс.

“Крестики-нолики” — логическая игра между двумя противниками на квадратном поле 3x3 клетки или большего размера. Один из игроков играет “крестиками”, второй — “ноликами”. Игроки по очереди ставят на свободные клетки поля 3x3 знаки (один — всегда “крестики”, другой — всегда “нолики”). Первый, кто выстроил в ряд три своих знака по вертикали, горизонтали или диагонали, выигрывает.

Достоверно известно, что игра “Рендзю” появилась в Древнем Китае во 2-м тысячелетии до н. э. В VII веке н. э. игра получила широкое распространение на всей территории Востока.

Правила игры “Рендзю”

Игра ведется на доске в клетку размером 15x15. В игре участвует два игрока: первый ходит черными камнями, второй — белыми. Задача — построить неразрывный ряд из пяти камней своего цвета по горизонтали, вертикали или диагонали. Однако, в отличие от игры “Крестики-нолики”, существует ряд ограничений ходов игрока, играющего черными камнями: ему нельзя строить “вилки” 3x3 и 4x4 и ряд из шести или более камней, а также любые вилки кратностью более двух. Для игрока белыми камнями ограничений не существует. Также в правилах игры предусмотрен пропуск хода. Ниже показаны выигрышные стратегии.

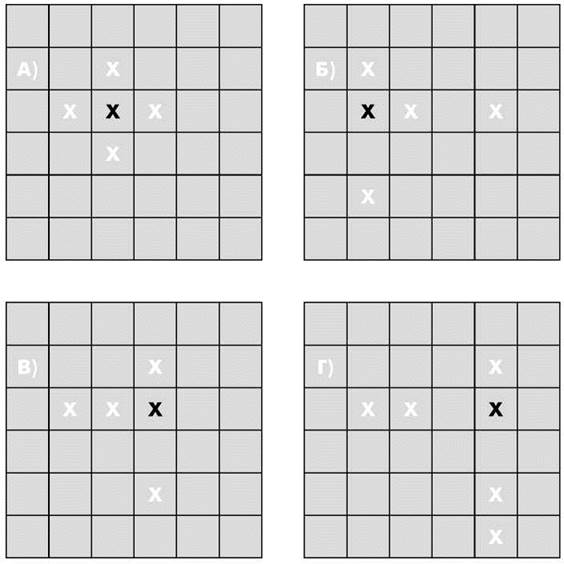
2. Определяем выигрышную стратегию для начинающего или противника в игровых задачах с камнями аналогично правилам игры “Рендзю” (задание № 1 рубрики “Подумаем вместе”). Закрепляем выигрышную стратегию, выполняя задания № 2—4 с учетом всех особенностей игры.

3. В рубрике “Проверь себя” предлагаем еще две игровые задачи. Учащиеся разбиваются на две группы и самостоятельно вырабатывают выигрышные стратегии.

В помощь учителю

Ответы к заданиям

“Проверь себя”

1. Выигрывает второй. Стратегия: “добавляй до числа, кратного 10”.

2. Иван Царевич назовет 1, 10, 100 и останется жив.

Оценка деятельности учащихся

Взаимопроверка. Учащиеся обмениваются выработанными стратегиями (№ 1—2 рубрики “Проверь себя”) и определяют оптимальную.