ТИПЫ ЧИСЛОВЫХ РЕБУСОВ. ЧИСЛОВЫЕ РЕБУСЫ, СОДЕРЖАЩИЕ ОПЕРАЦИИ СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ - РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ ЗАНЯТИЙ С ИСПОЛЬЗОВАНИЕМ ДИДАКТИЧЕСКИХ МАТЕРИАЛОВ

Цель: познакомить учащихся с основными правилами шифровки и дешифровки числовых ребусов.

Основное содержание

1. Знакомимся с типами числовых ребусов по виду шифровки.

2. Изучаем основные правила шифровки и дешифровки числовых ребусов.

3. Решаем числовые ребусы, содержащие операции сложения и вычитания.

4. Решаем числовые ребусы, содержащие операции умножения и деления.

Формы, методы и средства

Лекция, фронтальная работа, самостоятельная работа и соревнование в группах.

Проведение занятия

1. Знакомим учащихся с типами ребусов (ребусы в картинках и числовые ребусы). Решая ребусы в картинках, используем раздаточный иллюстративный материал.

2. Рассмотрим основные правила шифровки и дешифровки числовых ребусов.

При решении числовых ребусов, содержащих операции сложения, наиболее часто приходится пользоваться следующими свойствами операции сложения натуральных чисел:

1) если при суммировании двух k-значных чисел в сумме получается (k + 1)-значное число, то его наивысший десятичный знак равен единице;

2) если при суммировании двух одинаковых k-значных чисел в сумме получается k-значное число, то десятичный знак наивысшего разряда слагаемых не превосходит четырех.

Числовой ребус, содержащий операцию вычитания, можно заменить числовым ребусом, содержащим операцию сложения.

При дешифровке ребусов, содержащих операцию умножения, часто приходится пользоваться следующими правилами:

1) если в результате умножения некоторого числа на однозначное число получено исходное число, то множитель равен единице;

2) нуль не может быть крайней левой цифрой в числе, а результат умножения на нуль состоит из одних нулей;

3) если в результате умножения некоторого числа, не оканчивающегося нулем, на некоторое однозначное число в числе единиц получен нуль, то число единиц множимого и множителя есть пара чисел, одно из которых равно пяти, а второе — четное;

4) если произведение некоторого k-значного числа и числа, большего или равного пяти, дает k-значное число, то ясно, что множимое начинается с единицы.

Числовой ребус, содержащий операцию деления, можно заменить числовым ребусом, содержащим операцию умножения.

3. Фронтально решаем несколько заданий рубрики “Подумаем вместе”.

4. Предлагаем учащимся самостоятельно решить остальные задания рубрик “Подумаем вместе” и “Проверь себя”. Один ученик работает с обратной стороны доски. Остальные — в тетрадях. После того как все справились с заданием, проверяем. В случае ошибки на доске вызываются учащиеся из класса и следует комментарий учителя.

В помощь учителю

Ответы и решения к заданиям

Числовые ребусы, содержащие операции сложения и вычитания

“Подумаем вместе”

“Проверь себя”

1. 1967.

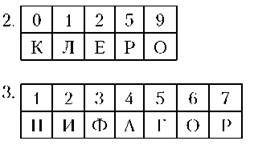
Числовые ребусы, содержащие операции умножения и деления

“Подумаем вместе”

“Проверь себя”

1. 23 ∙ 56 = 1288.

2. 74 ∙ 23 = 1702.

3. 926 ∙ 37 = 34 262.

4. 629 ∙ 93 = 58 497.

5. 452 ∙ 125 = 56 500.

6. 523 ∙ 637 = 333 151.

7. 528 ∙ 217 = 114 576.

Оценка деятельности учащихся

В конце занятия учащимся предлагается разделиться на две команды и устроить соревнование “Кто быстрее”. Учитель предлагает задания из рубрики “Проверь себя” и определяет количество баллов за каждый решенный числовой ребус. По истечении времени проверяются ответы. Выигрывает команда, набравшая большее количество баллов.