Периметр и площадь прямоугольника. Объём прямоугольного параллелепипеда - Материалы для подготовки к самостоятельным работам

Пример 1. Стороны прямоугольника равны 21 см и 11 см. Вычислим его: а) периметр; б) площадь.

Решение.

а) Вычислим периметр прямоугольника по формуле Р = 2 (а + b), где а и b — стороны прямоугольника: Р = 2 ∙ (21 + 11) = 64 (см).

б) Вычислим площадь прямоугольника по формуле S = ab, где а и b — стороны прямоугольника: S = 21 ∙ 11 = 231 (см²).

Ответ, а) 64 см; б) 231 см².

Пример 2. Три измерения прямоугольного параллелепипеда равны 25 см, 12 см, 8 см. Найдём:

а) объём прямоугольного параллелепипеда;

б) сумму площадей всех его граней.

Решение.

а) Вычислим объём прямоугольного параллелепипеда по формуле V = abc, где а, b и с — измерения прямоугольного параллелепипеда: V = 25 ∙ 12 ∙ 8 = 2400 (см³).

б) Вычислим сумму площадей всех граней прямоугольного параллелепипеда по формуле S = 2 (ab + bc + ac), где а, b и с — его измерения: S = 2 ∙ (25 ∙ 12 + 12 ∙ 8 + 25 ∙ 8) = 1192 (см²).

Ответ, а) 2400 см³; б) 1192 см².

Пример 3. Вычислим периметр шестиугольника, изображённого на рисунке 13.

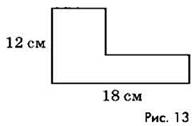
Решение. Периметр данного шестиугольника равен периметру прямоугольника со сторонами 12 см и 18 см (рис. 14), поэтому Р = 2 ∙ (12 + 18) = 60 (см).

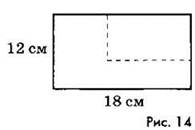
Ответ. 60 см.

Пример 4. Стороны прямоугольника увеличили в 2 раза. Во сколько раз увеличится площадь прямоугольника?

Решение. Пусть стороны прямоугольника имели длины а см и b см, его площадь была равна ab см². После увеличения в 2 раза стороны прямоугольника имеют длины 2а см и 2b см, а его площадь равна 2а ∙ 2b = 4аb см², т. е. площадь прямоугольника увеличилась в 4 раза.

Ответ. В 4 раза.