Математика - Дидактические материалы 5 класс - 2017 год
Углы, треугольники, многоугольники - Материалы для подготовки к самостоятельным работам
Пример 1. Сколько квадратов изображено на рисунке 10? Сколько прямоугольников изображено на рисунке 10?
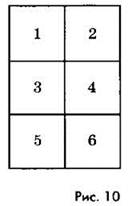
Решение. На рисунке 10 изображено 6 квадратов (маленьких), 2 квадрата, каждый из которых содержит 4 маленьких квадрата — 1, 2, 3, 4 и 3, 4, 5, 6. Больше квадратов нет. Всего 6 + 2 = 8 квадратов.
Все рассмотренные квадраты являются прямоугольниками, подсчитаем теперь число прямоугольников, не являющихся квадратами. На рисунке 10 изображено 7 прямоугольников, содержащих 2 маленьких квадрата, 2 прямоугольника, содержащие 3 маленьких квадрата, 1 прямоугольник, содержащий 6 маленьких квадратов. Других прямоугольников нет. Всего прямоугольников 8 + 7 + 2 + 1 = 18.
Пример 2. Сколько существует треугольников, вершинами которых являются вершины пятиугольника ABCDE (рис. 11)?

Решение. Найдём все треугольники с вершиной А. Это треугольники АВС, ABD, ABE, ACD, АСЕ, ADE — всего 6 треугольников. Теперь подсчитаем все треугольники, не имеющие вершины A: BCD, ВСЕ, BDE, CDE — их 4. Все треугольники в списках разные, других треугольников нет, следовательно, всего треугольников 6 + 4 = 10.
Число треугольников можно подсчитать иначе: для каждой из пяти вершин существует 6 треугольников, имеющих эту вершину (как при вершине А). Но всего треугольников не 5 ∙ 6 = 30, а в 3 раза меньше, так как каждый треугольник учтён трижды — для каждой своей вершины, т. е. всего треугольников 5 ∙ 6 : 3 = 10.
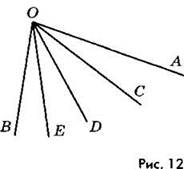
Пример 3. Внутри острого угла из его вершины провели три луча. Сколько новых углов образовалось внутри данного угла?
Решение. Образовалось: 4 угла, внутри которых нет ни одного луча (как угол АОС на рисунке 12), 3 угла, внутри которых есть один луч (как угол AOD на рисунке 12), 2 угла, внутри которых два луча (как угол АОЕ на рисунке 12). Три луча содержится только внутри данного угла, но он не новый. Всего образовалось 4 + 3 + 2 = 9 новых углов.