Измерение углов. Транспортир - Урок 3 - ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ - ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: учить строить, измерять и распознавать углы; познакомить со свойством углов треугольника.

Ход урока

I. Организационный момент

II. Определение темы урока

Сегодня на уроке мы продолжим изучение углов, будем работать с транспортиром.

III. Устный счет

1. На доске (слайде):

— Прочитайте записи.

— Дайте характеристику каждого утла.

— Мысленно проведите биссектрису каждого угла. На какие углы биссектриса разделила каждый угол?

— Найдите 20% каждого угла.

— Найдите 1/4 каждого угла.

2. Рассмотрите чертеж.

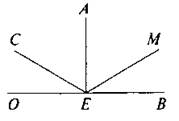
— Сколько разных углов вы видите на чертеже? (10.)

— Назовите каждый угол и дайте характеристику.

— Назовите все углы, градусная мера которых больше 90°, меньше 90°, равна 90°.

— Есть ли на чертеже луч, который является биссектрисой?

— Объясните свое предположение.

IV. Работа по теме урока

— Постройте прямой угол.

— Проведите отрезок так, чтобы получился треугольник.

— Узнайте градусную меру каждого утла.

— Найдите сумму углов.

(У всех учащихся разные треугольники. Поэтому на примере разных треугольников можно сделать вывод.)

— Что вы заметили?

— Какой вывод можно сделать? (Сумма углов треугольника равна 180°.)

— Это свойство углов треугольника. На его основе решаются геометрические задачи.

Сегодня мы решим некоторые из них.

С. 253, № 1666 (устно).

V. Решение геометрических задач

1. С. 253, № 1663.

(Следует объяснить учащимся, что при решении таких задач рисунок надо делать обязательно. Он является частью решения геометрической задачи.)

— Что дано в этой задаче?

— Что требуется узнать?

(Задача оформляется на доске.)

а) Дано: ∠АОВ — развернутый

ОС — луч

∠AОС > ∠СОВ в 3 раза

Найдите: ∠АОС и ∠СОВ

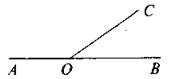
— Такие задачи лучше решать алгебраически.

— Что обозначим через х?

Пусть градусная мера угла СОВ будет х.

Тогда градусная мера угла АОС будет 3х.

Сумма этих углов х + 3х.

А по условию 180° (так как сумма образует развернутый угол).

Значит, можем составить уравнение:

х + 3х = 180

4х = 180

х = 180 : 4

х = 45.

45° — градусная мера угла СОВ.

45° ∙ 3 = 135° — градусная мера угла АОС.

— Как иначе можно найти градусную меру угла АОС? (180 - 45 = 135.)

б) (Разбирается и оформляется аналогично.)

Пусть градусная мера угла СОВ будет х.

Тогда градусная мера угла АОС будет х + 60.

Сумма этих углов равна х + х + 60.

А по условию сумма этих углов равна развернутому углу, т. е. 180°.

Значит, можем составить уравнение:

х + х + 60 = 180

2х + 60 = 180

2х = 180 - 60

2х = 120

х = 120 : 2

х = 60.

60° — градусная мера угла СОВ.

60°+ 60° = 120°.

2. С. 253, № 1664 (работа в паре).

Проверка

Пусть градусная мера угла СОВ будет х.

Тогда градусная мера утла АОС будет 5х.

Сумма этих углов х + 5х.

А по условию сумма этих углов составляет прямой угол, т. е.

Значит, можем составить уравнение:

х + 5х = 90

6х = 90

x = 90 : 6

x = 15

15° — градусная мера угла СОВ.

15° ∙ 5 = 75° — градусная мера угла AОС.

— Как иначе можно найти градусную меру угла AОС? (90° - 15° = 75°.)

VI. Самостоятельная работа

(Самостоятельная работа проводится по карточкам, в которые учащиеся вписывают ответы.)

— Зная, что сумма углов треугольника равна 180°, найдите градусную меру неизвестного угла.

Вариант 1