Функции у = х² и у = х³ и их графики - ОДНОЧЛЕНЫ - СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Цель: рассмотреть свойства функций у = х² и у = х³ и их графики.

Планируемые результаты: научиться строить графики функций у = х² и у = х².

Тип уроков: урок изучения нового материала.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Перемножьте одночлены 3х²у, -0,5х³у² и 2ху⁴.

2. Возведите одночлен 2а³b²с в квадрат и в куб.

3. Представьте выражение в виде одночлена стандартного вида и определите его степень.

Вариант 2

1. Перемножьте одночлены 2ху², 3х⁴у³ и -0,5х²у³.

2. Возведите одночлен 3ab³c² в квадрат и в куб.

3. Представьте выражение в виде одночлена стандартного вида и определите его степень.

III. Работа по теме уроков

Зависимость площади квадрата S от его стороны a (S = а²), зависимость кинетической энергии Е тела массой m от его скорости зависимость потенциальной энергии Е пружины от длины l, на которую она растянута, где k — коэффициент упругости пружины, и т. д. являются примерами функции у = х². Рассмотрим таблицу значений такой функции и на основании ее данных построим график функции.

x	-3	-2,5	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2	2,5	3
y	9	6,25	4	2,25	1	0,25	0	0,25	1	2,25	4	6,25	9

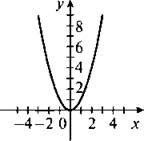
График функции у = х² называется параболой. Рассмотрим свойства такой функции.

1. Область определения функции — все значения х. Действительно, любое число х можно возвести во вторую степень (в квадрат).

2. Область значений функции — все значения у ≥ 0. При возведении в квадрат любого числах х ≠ 0 получаем положительное число. При возведении в квадрат нуля получаем нуль. Поэтому значения у ≥ 0 и график функции расположены не ниже оси абсцисс.

3. График функции проходит через начало координат.

4. Противоположным значениям х соответствует одно и то же значение у, так как (-х)² = х² при любом х. Поэтому график функции симметричен относительно оси ординат. Заметим, что такие функции называются четными.

Рассмотрим кубическую зависимость у = х³. Зависимость объема V куба от его стороны а (V = а³), зависимость объема V шара от его радиуса где п = 3,14, и т. д. являются именно такими зависимостями. Составим таблицу значений функции у = х³ и на основании ее данных построим график.

x	-2	-1,5	-1	-0,5	0	0,5	1	1,5	2
y	-8	-3,38	-1	-0,13	0	0,13	1	3,38	8

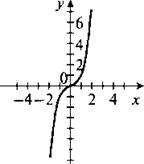
Рассмотрим свойства такой функции.

1. Область определения функции — все значения х. Действительно, любое число х можно возвести в третью степень (в куб).

2. Область значений функции — все значения у. При возведении в куб отрицательного числа получаем отрицательное число, при возведении нуля — нуль, при возведении положительного числа — положительное число.

3. График функции проходит через начало координат.

4. Противоположным значениям х соответствуют противоположные значения у, так как (-х)³ = (-1)³ ∙ х³ = -х³ при любом х. Поэтому график функции симметричен относительно начала координат.

Заметим, что такие функции называются нечетными.

IV. Задания на уроках

№ 484, 487, 488, 492 (а), 493, 494 (б), 496 (а).

V. Контрольные вопросы

— Нарисуйте эскиз графика функции у = х².

— Перечислите свойства функции у = х².

— Нарисуйте эскиз графика функции у = х³.

— Перечислите свойства функции у = х³.

— Дайте определение четной и нечетной функций.

VI. Творческие задания

1. Пользуясь графиком соответствующих функций, сравните числа:

2. Среди приведенных укажите четные и нечетные функции:

(Ответ: четные функции — а, в, д, е, нечетные функции — б, г, ж, з, л.)

3. Постройте график функции:

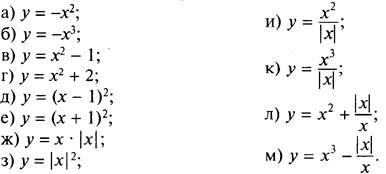
Укажите четные и нечетные функции.

VII. Подведение итогов уроков

Домашнее задание

№ 485, 489, 490, 492 (б), 494 (а), 496 (б).